Методы классификации
Содержание
В этом мире наша первая обязанность состоит в том, чтобы устраивать островки порядка и системы.
Норберт Винер
Классификация является основой человеческой умозрительной деятельности… Классификация является фундаментальным процессом научной деятельности, поскольку системы классификаций содержат понятия, необходимые для разработки теорий в науке.
М.С.Олдендерфер, Р.К.Блэшфилд, «Кластерный анализ»
К задачам классификации относятся задачи, в которых необходимо разделить некоторые объекты или явления на однородные группы (классы) при наличии совокупности свойств, описывающих эти объекты (свойство не одно — их много). Задачи разделяют на две группы:
- Определение принадлежности объекта к одной из групп, которые заданы обучающими выборками (дискриминантный анализ).
- Разбиение множества объектов на однородные группы при отсутствии обучающих выборок (кластерный анализ).
Очень часто важной сопутствующей задачей является определение минимального информативного подмножества описывающих объект переменных, достаточного для разделения объектов на однородные группы.
К задачам классификации относится, например, установление диагноза по результатам анализа и обследования (дискриминантный анализ). А также — выявление групп больных, которые можно считать однородными по совокупности их индивидуальных особенностей (включая течение болезни и процесс лечения), что позволит лучше подбирать курс лечения (кластерный анализ).
5.1. Кластерный анализ
Главная цель кластерного анализа — нахождение групп схожих объектов в выборке данных.
М.С. Олдендерфер, Р.К. Блэшфилд, «Кластерный анализ»
Древняя китайская классификация животных.
Животные подразделяются на: а) принадлежащих императору; б) набальзамированных; в) дрессированных; г) молочных поросят; д) сирен; е) сказочных; ж) бродячих собак; з) включенных в данную классификацию; и) дрожащих как сумасшедшие; к) неисчислимых; л) нарисованных самой лучшей верблюжьей кисточкой; м) других; н) тех, которые только что разбили цветочную вазу и о) тех, которые издали напоминают мух.
Хорхе Луис Борхес, «Другие исследования»
5.1.1. Теоретические сведения
Для разделения выборки на однородные подвыборки используются методы кластерного анализа. Кластерным анализом называется совокупность многомерных статистических процедур, которая позволяет упорядочить объекты по однородным группам.
Назначение
С помощью кластерного анализа исследуемую совокупность объектов, представленную в виде матрицы объекты-свойства разбивают на небольшое количество однородных в некотором смысле групп (их количество заранее может быть известно или неизвестно). Обучающей выборки в кластерном анализе не существует.
Матрица «объекты-свойства» имеет вид , где хij — значение j-го свойства для объекта с номером i. То есть имеется n объектов и m свойств, описывающих эти объекты.
Классическим примером такого разделения на кластеры является качественно разная эффективность лекарственного препарата (выздоровление или ухудшение состояния) в зависимости от пола больного. Разрыв пространства существования фактора может возникать также при определенной комбинации некоторой совокупности независимых переменных. Однако построить качественную и имеющую физический смысл модель для разрывной области невозможно по объективным причинам. Нужно попытаться найти фактор или комбинацию факторов, ответственных за разрыв и строить модели для каждой из выделенных подобластей отдельно.То есть, одна модель описывает влияние препарата на организм мужчины, другая — на организм женщины и т.п.
На рис. 5.1. показана диаграмма рассеивания, на которой видно, что данные распадаются на две разделенные в пространстве подвыборки (кластера), несвязанные между собой.
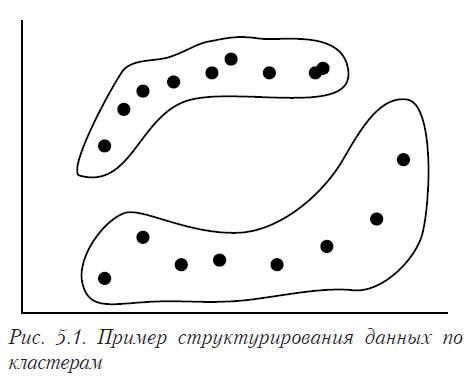
Общая схема решения задачи
Решение задачи кластерного анализа выполняется в следующей последовательности:
- Формирование выборки для анализа.
- Выбор совокупности признаков, характеризующих объект.
- Выбор меры сходства (расстояния) между объектами и расчет их.
- Формирование кластеров.
- Анализ полученной информации.
Большинство алгоритмов кластерного анализа относится к так называемым агломеративным процедурам, в которых сначала объединяют в группы самые близкие объекты, а затем к ним присоединяют более дальние.
Возможные меры сходства (расстояния между объектами)
Для определения сходства между объектами обычно пользуются понятием расстояния dij(Oi,Oj) между объектами Oi и Oj. Чем меньше расстояние, тем больше похожими считаются объекты. Для того, чтобы быть пригодной для определения расстояния между объектами, предлагаемая мера должна обладать следующими свойствами:
- симметрии dij(Oi,Oj) = dji(Oj,Oi);
- минимального расстояния объекта к самому себе dii(Oi,Oi) = 0;
- монотонного изменения dii в описываемом пространстве;
- смысловой интерпретации меры (желательна).
Наиболее часто в кластерном анализе используются меры, базирующиеся на обобщенном расстоянии Махаланобиса, которое задается формулой
![]()
Здесь Х — вектор наблюдений, L — симметричная неотрицательно-определенная матрица весовых коэффициентов (обычно диагональная), S — ковариационная матрица совокупности, из которой извлечены наблюдения.
Реально используются следующие частные виды расстояний
Евклидово расстояние
Это привычное нам расстояние между объектами. Вычисляется по формуле
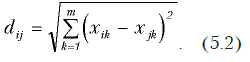
Обычно это расстояние используется при выполнении следующих условий:
- Компоненты Х взаимно независимы, имеют одну и ту же дисперсию.
- Компоненты однородны по физическому смыслу.
Если разные свойства, характеризующие объект, имеют различную важность и ее можно оценить (хотя бы с помощью экспертов) используется взвешенное евклидово расстояние:
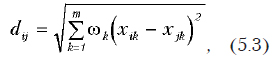
где wk — весовой коэффициент для k-го свойства. При этом обычно принимается 0 £ wk £1 для всех k.
Хеммингово расстояние
Оно иногда называется расстоянием городских кварталов (то есть путь от перекрестка до перекрестка не напрямую, а только по улицам). Определяется по формуле
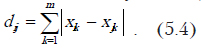
Расстояние между классами
Вышеуказанные меры определяют расстояние между объектами. Но для выполнения кластеризации необходимо установить, что считать расстоянием между кластерами. Обычно используются следующие меры близости групп (расстояний между кластерами):
· Расстояние, вычисляемое по принципу «ближайшего соседа».
Вычисляется по формуле
![]()
Является минимальным расстоянием между парой объектов, каждый из которых состоит в другом кластере.
· Расстояние, вычисляемое по принципу «дальнего соседа».
Для определения этого расстояния служит формула
![]()
Является максимальным расстоянием между парой объектов, каждый из которых состоит в другом кластере.
· Расстояние, вычисляемое по «центрам тяжести» кластеров.
Вычисляется по формуле
![]()
где — среднее арифметическое векторных наблюдений, которые входят в кластер St. То есть это расстояние между «центрами тяжести» соответствующих кластеров.
· Расстояние, вычисляемое по принципу «средней связи» между кластерами.
Для его вычисления служит формула

Является арифметическим средним расстоянием всех возможных пар комбинаций между объектами, входящими в различные кластеры.
Качество разбиения на классы
В связи с существованием достаточно большого количества различных процедур кластерного анализа, для сравнения качества разбиения на классы используется ряд функционалов качества. Наиболее употребительные из них:
· Сумма внутриклассовых дисперсий расстояний —
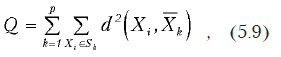
где р — количество кластеров.
· Сумма попарных внутриклассовых расстояний —

где р — количество кластеров.
Примечание
- Цель кластерного анализа — поиск существующих реальных структур данных.
- Разные процедуры кластерного анализа могут для одних и тех же данных давать различное разбиение на кластеры (как по их количеству, так и по составу).
- Большинство методов кластерного анализа не имеют строгого статистического обоснования.
5.1.2. Описание применяемого алгоритма
Рассмотрим процедуру кластерного анализа, предлагаемого для обработки данных. Существуют две ее разновидности, которые могут давать различное разбиение на кластеры. Выбирать подходящую разновидность следует исходя из постановки задачи. Если это невозможно, необходимо провести разбиение двумя способами и попытаться определить, какой из них больше соответствует фактически существующим структурам данных. При изотоническом разбиении группы объектов состоят из однородных по уровню значений, а при изоморфном в группы включаются объекты близкие по структуре, то есть, те, в которых пропорции признаков мало отличаются. Это означает, что различные способы разбиения могут давать различное объединение по группам. Например, у нас есть данные, которые характеризуют распределение прибыли фирм на расширение производства, научные исследования, социальные выплаты и пр. Тогда при изотоническом разбиении группы будут состоять из фирм, в которых уровни прибыли близки, а при изоморфном — в однородные группы будут включаться те компании, в которых структуры распределения прибыли сходны.
В обоих способах признаки сначала преобразуют таким образом, чтобы не было единиц измерения и размах шкалы был одинаковым.
Изотоническое разбиение
Для нормирования шкал необходимо выполнить следующие преобразования.
Сначала каждое значение признака заменяется на вычисленное по формуле
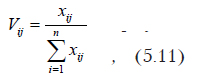
где xij — значение j-го признака для i-го объекта.
После этого каждому объекту ставится в соответствие одно число, вычисленное следующим образом:
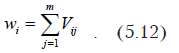
Расстояния между двумя объектами определяются по формуле
![]()
Изоморфическое разбиение
Сначала выполняют нормирование шкал по формуле
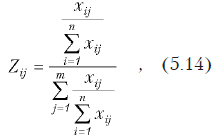
где xij — значение j-го признака для i-го объекта..
Расстояния определяются по формуле
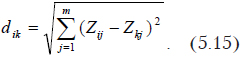
В изоморфном преобразовании расстояние будет минимальным в том случае, когда векторы коллинеарные, и максимальным, — если они перпендикулярны.
Разбиение на кластеры
После определения расстояний с помощью метода шаров возможно разбиение на группы. Затем, построив дендриты, можно определить форму следа данных. Под следом понимается пространственная форма, которую принимает совокупность экспериментальных точек. В методе шаров критический радиус (расстояние, которое определяет, принадлежит ли объект данному кластеру) вычисляется как
![]()
То есть, по каждому объекту выбирается минимальное расстояние до ближайшего к нему объекта. Затем из этих минимальных расстояний выбирается максимальное. Тогда, объекты, расстояния между которыми меньше критического, принадлежат к одному кластеру. На рис. 5.2 показано разбиение на кластеры с использованием метода шаров. В один кластер включаются объекты, расстояние между которыми меньше критического. Недостаток метода в том, что кластеры получаются несколько искусственными (шаровидной формы).

Построение дендритов и определение связности
Первичное разбиение на кластеры (описанное выше) позволяет получить кластеры шаровидной или эллипсовидной формы. Поскольку при выполнении практических задач такие кластеры встречаются далеко не всегда (и нередки случаи, когда след имеет С- или S-образную, а то и более сложную форму), то на следующем этапе обычно выполняют построение дендритов и определение связности в системе кластеров. Это позволяет объединить первоначальные кластеры в более сложные структуры, которые в большей степени отвечают их реальной форме.
То есть на этом этапе определяется, являются ли наши выделенные кластеры полностью несвязными или образуют какую-либо связную структуру.
Для этого сначала определяют расстояния между кластерами:
![]()
расстояние между двумя кластерами равно минимальному расстоянию между двумя объектами, входящими в эти кластеры.
Критическое расстояние, это такое расстояние, при превышении которого кластеры считаются несвязными, принимается равным максимальному расстоянию между соседними элементами в одном кластере или рассчитывается по следующей формуле
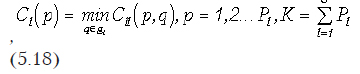
где
Cll(p, q) — расстояние между элементами p и q, принадлежащими к l-й группе (кластеру); Cl(p) — расстояние от элемента p до соседнего элемента в группе l; Pl — количество элементов в l-й группе; G — количество групп.
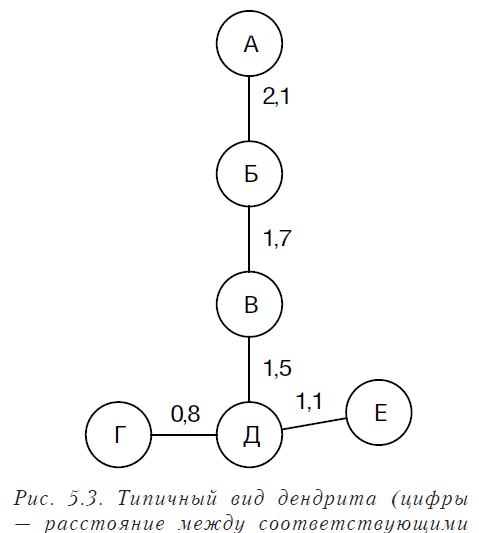
После определения расстояний кластеры последовательно объединяются в группы, таким образом, чтобы в конечном результате получить дендрит, объединяющий всю совокупность данных. Выполняется это следующим образом: каждый кластер связывается с ближайшим к нему. Обычно получившийся дендрит имеет форму цепочки, но возможны и более сложные формы: «дерево», «розетка», «амеба» и т.п.
После построения дендрита, объединяющего все данные, на основе анализа критического расстояния разрывают связи между кластерами, расстояние между которыми больше критического. В результате получается набор дендритов, несвязных между собой, но кластеры, входящие в каждый дендрит образуют связную подвыборку. Данные, входящие в такую подвыборку, можно аппроксимировать с помощью регрессионного анализа.
Если окончательный связный дендрит имеет форму «розетка» или «амеба» (рис. 5.3), его следует разделить на более простые, поскольку получить в такой области регрессионную модель затруднительно. Обычно в таких случаях мы имеем дело не с одним следом, а с пересечением нескольких разных следов. Область пересечения у них общая, а в остальном — это отдельные области пространства (рис. 5.4).

5.1.3. Программа обработки и ее вызов
В связи с отсутствием в Excel средств кластерного анализа, предлагаем набор программ, которые вы можете ввести в свою книгу.
Option Base 1
Sub claster_1()
Dim s_1()
Dim s_2()
Dim s_3()
Dim mat_res()
Dim mas_min() As Double
Set myCELL = Application.InputBox( _
prompt:=»Выберите исходную матрицу данных», _
Type:=8)
Set myCell2 = Application.InputBox( _
prompt:=»Выберите ячейку, с которой будут выводится результаты», _
Type:=8)
Set myCell3 = Application.InputBox( _
prompt:=»Выберите ячейки, содержащие имена объектов», _
Type:=8)
Num_row = myCELL.Rows.Count ‘Вычисление количества строк
Num_col = myCELL.Columns.Count ‘Вычисление количества столбцов
‘ Выполним нормировку исходных данных
ReDim s_1(Num_col)
ReDim s_2(1 To Num_col, 1 To Num_row)
‘Вычисление суммы по столбцам и помещение ее в массив s_1
For i = 1 To Num_col
s_1(i) = Application.Sum(myCELL.Columns(i))
For j = 1 To Num_row
s_2(i, j) = myCELL.Columns(i).Cells(j) / s_1(i)
Next j
Next i
ReDim s_3(Num_row)
‘Расчет длин векторов
ReDim mas_min(Num_row)
For i = 1 To Num_row
s_3(i) = 0
mas_min(i) = 1
For j = 1 To Num_col
s_3(i) = s_3(i) + s_2(j, i)
Next j
Next i
ReDim mat_res(1 To Num_row, 1 To Num_row)
‘Расчет для матрицы расстояний массива минимальных значений
For i = 1 To Num_row
For j = 1 To Num_row
mat_res(i, j) = Abs(s_3(i) — s_3(j))
If mat_res(i, j) < 1.1E-15 Then mat_res(i, j) = 0
If i <> j Then
If mas_min(i) > mat_res(i, j) Then mas_min(i) = mat_res(i, j)
End If
Next j
Next i
‘Поиск максимального с минимальных
Max_min = 0
For i = 1 To Num_row
If Max_min < mas_min(i) Then Max_min = mas_min(i)
Next i
‘Формирование и вывод изотонической матрицы расстояний
myCell2.Offset(0, 1).Value = «Матрица изотонических расстояний»
For i = 1 To Num_row
myCell2.Offset(1, i).Value = myCell3.Cells(i)
myCell2.Offset(1, i).Font.Italic = True
myCell2.Offset(1, i).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(i + 1, 0).Value = myCell3.Cells(i)
myCell2.Offset(i + 1, 0).Font.Italic = True
myCell2.Offset(i + 1, 0).Borders(xlEdgeRight).LineStyle = xlDouble
Next i
myCell2.Offset(1, 0).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(1, 0).Borders(xlEdgeRight).LineStyle = xlDouble
For i = 1 To Num_row
For j = 1 To Num_row
myCell2.Offset(i + 1, j).Value = mat_res(i, j)
Next j
Next i
myCell2.Offset(Num_row + 2, 0).Value = «min»
myCell2.Offset(Num_row + 2, 0).Borders.Item(xlEdgeTop).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, 0).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, 0).Borders(xlEdgeRight).LineStyle = xlDouble
For i = 1 To Num_row
myCell2.Offset(Num_row + 2, i).Value = mas_min(i)
myCell2.Offset(Num_row + 2, i).Borders.Item(xlEdgeTop).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, i).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
Next i
myCell2.Offset(Num_row + 3, 0).Value = «Критическое значение = »
myCell2.Offset(Num_row + 3, 3).Value = Max_min
‘ Поиск объектов, используя метод шаров
End Sub
Sub claster_2()
Dim s_1()
Dim s_2()
Dim s_3()
Dim mat_res()
Dim mas_min() As Double
Set myCELL = Application.InputBox( _
prompt:=»Выберите исходную матрицу данных», _
Type:=8)
Set myCell2 = Application.InputBox( _
prompt:=»Выберите ячейку, с которой будут выводится результаты», _
Type:=8)
Set myCell3 = Application.InputBox( _
prompt:=»Выберите ячейки, содержащие имена объектов», _
Type:=8)
Num_row = myCELL.Rows.Count ‘Вычисление количества строк
Num_col = myCELL.Columns.Count ‘Вычисление количества столбцов
‘ Выполним нормировку исходных данных
ReDim s_1(Num_col)
ReDim s_2(1 To Num_col, 1 To Num_row)
‘Вычисление суммы по столбцам и помещение ее в массив s_1
For i = 1 To Num_col
s_1(i) = Application.Sum(myCELL.Columns(i))
For j = 1 To Num_row
s_2(i, j) = myCELL.Columns(i).Cells(j) / s_1(i)
Next j
Next i
ReDim s_3(Num_row)
‘Расчет длин векторов
ReDim mas_min(Num_row)
For i = 1 To Num_row
s_3(i) = 0
mas_min(i) = 1
For j = 1 To Num_col
s_3(i) = s_3(i) + s_2(j, i)
Next j
Next i
‘Преобразование матрицы длин векторов
For i = 1 To Num_row
For j = 1 To Num_col
s_2(j, i) = s_2(j, i) / s_3(i)
Next j
Next i
ReDim mat_res(1 To Num_row, 1 To Num_row)
‘Расчет матрицы расстояний и массива минимальных значений
For i = 1 To Num_row
For j = 1 To Num_row
s_tmp = 0
For n = 1 To Num_col
s_tmp = s_tmp + (s_2(n, i) — s_2(n, j)) ^ 2
Next n
mat_res(i, j) = Sqr(s_tmp)
If i <> j Then
If mas_min(i) > mat_res(i, j) Then mas_min(i) = mat_res(i, j)
End If
Next j
Next i
‘Поиск максимального c минимальным
Max_min = 0
For i = 1 To Num_row
If Max_min < mas_min(i) Then Max_min = mas_min(i)
Next i
‘Формирование и вывод изоморфической матрицы расстояний
myCell2.Offset(0, 1).Value = «Матрица изоморфических расстояний»
For i = 1 To Num_row
myCell2.Offset(1, i).Value = myCell3.Cells(i)
myCell2.Offset(1, i).Font.Italic = True
myCell2.Offset(1, i).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(i + 1, 0).Value = myCell3.Cells(i)
myCell2.Offset(i + 1, 0).Font.Italic = True
myCell2.Offset(i + 1, 0).Borders(xlEdgeRight).LineStyle = xlDouble
Next i
myCell2.Offset(1, 0).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(1, 0).Borders(xlEdgeRight).LineStyle = xlDouble
For i = 1 To Num_row
For j = 1 To Num_row
myCell2.Offset(i + 1, j).Value = mat_res(i, j)
Next j
Next i
myCell2.Offset(Num_row + 2, 0).Value = «min»
myCell2.Offset(Num_row + 2, 0).Borders.Item(xlEdgeTop).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, 0).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, 0).Borders(xlEdgeRight).LineStyle = xlDouble
For i = 1 To Num_row
myCell2.Offset(Num_row + 2, i).Value = mas_min(i)
myCell2.Offset(Num_row + 2, i).Borders.Item(xlEdgeTop).LineStyle = xlDouble
myCell2.Offset(Num_row + 2, i).Borders.Item(xlEdgeBottom).LineStyle = xlDouble
Next i
myCell2.Offset(Num_row + 3, 0).Value = «Критическое значение = »
myCell2.Offset(Num_row + 3, 3).Value = Max_min
End Sub
5.1.4. Пример
Развитие различных баз данных в поликлиниках, медицинских НИИ и больницах позволяет накапливать большой объем информации о больных, включающей как антропологические и социальные сведения, так и достаточно полные данные о заболеваниях и их лечении в динамике. Но для того, чтобы вся эта информация действительно была полезной и ее можно было бы использовать на практике, необходимы средства ее обработки.
Одна из первоочередных задач, возникающая при обработке, — формирование из данных однородных групп, внутри которых затем выполнять поиск закономерностей. Необходимость использования для этого процедур кластерного анализа связана с тем, что большое количество факторов и разнородность самой информации делают выбор признаков классификации неочевидным.
Рассмотрим для примера условную задачу. На рис. 5.5 представлены исходные данные. При этом Р1…Р6 — пациенты, а Х1…Х4 — факторы, описывающие их состояние.
Для запуска кластерного анализа входим в меню и последовательно выбираем Сервис, а затем Макрос. Появляется окно, приведенное на рис. 5.6. В этом окне выбираем одну из двух имеющихся процедур кластерного анализа (в данном случае — claster_2). После этого процедура кластерного анализа запускается и начинает запрашивать у пользователя необходимые для работы данные.
Первым появляется окно, изображенное на рис. 5.7.

В этом окне (рис. 5.7) вы должны указать диапазон ячеек, в которых размещены исходные данные.
После этого появляется окно (рис. 5.8), в котором необходимо ввести ссылку на ячейку, начиная с которой будут выводиться результаты. Эта ячейка будет левой верхней в поле результатов.


Разбиение на кластеры и формирование следа выполняется вручную. Для разбиения на кластеры необходимо сравнить расстояние от каждого из объектов до всех остальных с критическим. Мы видим, что наше множество распадается на 4 кластера. В первый входят пациенты Р1 и Р2, во второй — Р4 и Р5, в третий — Р3 и в четвертый — Р6.
Попробуем теперь определить форму следа в пространстве. Для этого сначала сформируем пары ближайших объектов (см. табл. 5.1).
Пары ближайших объектов
Таблица 5.1
| Объекты | Расстояние | |
| Р1 | Р2 | 0 |
| Р2 | Р1 | 0 |
| Р3 | Р6 | 0,04714 |
| Р4 | Р5 | 0 |
| Р5 | Р4 | 0 |
| Р6 | Р3 | 0,04714 |
Образовались три первичные пары: Р1 и Р2, Р3 и Р6, Р4 и Р5. На следующем шаге мы должны их всех объединить в одну выборку. Для этого необходимо найти, какие из элементов каждой пары ближе к какому-либо из элементов другой. Третья ближе всего к четвертой и пятой (0,04714), а пятая — к первой и второй (0,117851). Таким образом, построенный на наших данных дендрит будет иметь следующую форму (рис. 5.11)
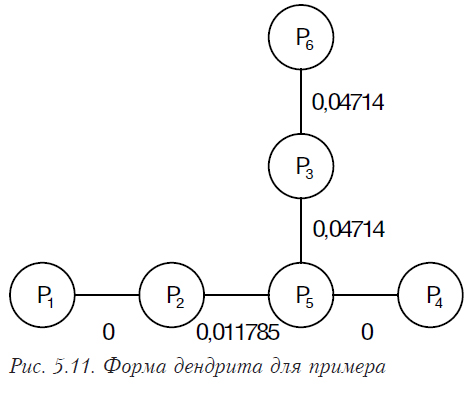
Критическое расстояние между кластерами вычисляется по формуле (5.18.) Оно будет равно (0+0,04714+0+0,117851+0,04714)/5 = 0,04243
Таким образом, мы разрываем расстояния, которые превышают критическое. В результате получим те же четыре кластера, которые были первоначально. Такое разделение не является однозначным. В ряде случаев к нему добавляется среднеквадратическое отклонение расстояний, умноженное на коэффициент 1 или 2. Среднеквадратическое отклонение расстояний для нашего примера равно 0,046547. Следовательно, критическое расстояние будет: 0,04243+0,046547=0,088977. В этом случае наша выборка распадается на два кластера: в один входят пациенты Р1 и Р2, в другой — Р4, Р6, Р3 и Р6.
5.2. Дискриминантный анализ
Группа экспертов исследует возможность переговоров с террористами, захватившими заложников. Их интересуют те особенности ситуации, при которых возможно безопасное освобождение заложников, даже если требования террористов не выполнены. … Дискриминантный анализ может обеспечить получение необходимых данных.
У.Р. Клекка, «Дискриминантный анализ»
5.2.1. Теоретические сведения
Дискриминантный анализ позволяет изучать различия между двумя или более группами объектов по нескольким переменным одновременно. Каждая группа объектов называется классом. Классы рассматриваются как значения некоторой классифицирующей переменной, измеренной по шкале наименований.
Если классифицирующая переменная зависит от дискриминантных, то в этом случае дискриминантный анализ является аналогом многофакторного регрессионного анализа, когда отклик измеряется по шкале наименований. Например, дискриминантные переменные описывают состояние больного и методику лечения, а переменная, классифицирующая показатель вида: выздоровел — не выздоровел.
В случае, когда дискриминантные переменные зависят от классифицирующей, т.е. принадлежность объекта к определенному классу вызывает изменения одновременно в нескольких переменных, дискриминантный анализ является аналогом обобщенного многомерного дисперсионного анализа. Например, классифицирующая переменная — заболевания, а дискриминантные переменные, на основании которых нужно поставить диагноз, характеризуют состояние больного.
В дискриминантном анализе различают две задачи: интерпретации и классификации. Задача интерпретации — определение количества и значимости дискриминантных функций, а также их значений для объяснения различий между классами. Задача классификации — определение класса, к которому принадлежит новый объект.
В дискриминантном анализе, в отличие от кластерного, имеется обучающая выборка, в которой известно к каким классам относятся объекты. По обучающей выборке необходимо выстроить правила, которые в дальнейшем позволят нам определять, к какому классу относятся новые объекты.
Назначение
Изучение различий между двумя и более группами объектов одновременно по нескольким описывающим их переменным. Позволяет по обучающей выборке получит правила (формулы), по которым определяется принадлежность объекта к определенной группе.
Предпосылки
- Объекты (наблюдения) принадлежат к двум или большему числу классов.
- В каждом классе есть как минимум два объекта.
- Число дискриминантных переменных не должно быть больше количества объектов минус два.
- Дискриминантные переменные должны измеряться в шкале интервалов или шкале отношений.
- Дискриминантные переменные должны быть линейно независимы.
- Дискриминантные переменные должны быть распределены по многомерному нормальному закону распределения (то есть каждая переменная имеет нормальный закон распределения при фиксированных остальных переменных).
- Ковариационные матрицы классов приблизительно равны между собой.
Решение задачи для случая двух классов
Наиболее распространенным (и более простым для решения) является случай двух классов.
Есть два класса, объекты характеризуются р переменными. Для первого класса сформирована выборка Х, объемом n1, для второго — Y объемом n2.
- Рассчитываются средние значения по каждой переменной для каждой выборки (класса) и .
- Определяются оценки ковариационных матриц для каждого класса Sx и Sy. и .
- Рассчитывается несмещенная оценка объединенной ковариационной матрицы.

- Находится матрица S-1, обратная к
- Рассчитывается вектор оценок коэффициентов дискриминантной функции .
- Определяются оценки векторов дискриминантных функций для исходных переменных Ux=XA и Uy=YA.
- Вычисляются средние значения оценок дискриминантных функций и .
- Определяется дискриминантная константа .
Обратите внимание на п.4, 5. Именно так предлагается решать задачу практически во всех книгах. Эти два пункта, по сути, описывают решение системы уравнений относительно А. Нахождение же обратной матрицы, во-первых, требует в три раза больше вычислительных операций, чем решение системы уравнений; во-вторых, при плохо обусловленной исходной матрице результаты неустойчивы [12]. В связи с этим в предлагаемом алгоритме в п.4, 5 выполняется решение системы линейных уравнений методом LU-разложения [16].
Для того, чтобы определить, к какому классу принадлежит какое-либо наблюдение Z (объект), необходимо сначала вычислить для него оценку дискриминантной функции . Если это значение больше или равно константе С, то новый объект относится к классу Х, если меньше — к классу Y (при ).
Последовательность решения задачи для общего случая k классов
Каноническая дискриминантная функция в этом случае имеет общий вид
![]()
где fki — значение канонической дискриминантной функции для i-го объекта в k-м классе; uj — искомые коэффициенты дискриминантной функции; Xjki — значение дискриминантной переменной Xj для i-го объекта в классе k. Функция строится таким образом, чтобы ее средние значения для различных классов как можно больше различались. При этом совокупность функций должна образовывать ортогональное пространство, то есть функции независимы друг от друга. Из этого следует, что количество функций не может быть больше количества классов минус 1 или числа дискриминантных переменных (в зависимости от того, какая из этих величин меньше).
Задача решается в несколько этапов.
- Построим матрицу Т, элементы которой определяются по формуле

где Xjki — значение дискриминантной переменной Xj для i-го объекта в классе k, — среднее значение для переменной j по всем классам, n — общее количество наблюдений по всем классам, K — число классов.
- Вычисляем матрицу W, которая определяет степень разброса внутри классов. Элементы этой матрицы находятся по формуле

Здесь — средняя величина переменной j в k-м классе. Остальные обозначения аналогичны обозначениям из предыдущей формулы.
- Вычисляем матрицу B = T – W, элементы определяются как bjl = tjl – Wjl .
- Решаем систему уравнений

Здесь l — собственное значение (чем оно больше, тем больше групп будет разделять соответствующая дискриминантная функция). Построенная на его базе каноническая корреляция показывает степень зависимости между дискриминантной функцией и классами, а квадрат ее (корреляции) h2 показывает долю дисперсии дискриминантной функции, которая объясняется разбиением на классы.
Для получения единственного решения вводится дополнительное ограничение
.
- Полученные коэффициенты нормируем по формуле . При этом .
Коэффициенты ui называются нестандартными, поскольку зависят от единиц измерения переменных. Поэтому часто переходят к стандартным коэффициентам, которые показывают относительный вклад переменной, независящий от шкалы измерения. Переход к стандартным коэффициентам осуществляется по формуле:
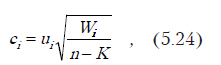
где n — общее число наблюдений, K — число классов (групп), Wii — диагональный элемент матрицы оценки рассеивания, вычисленный по формуле (5.22).
Величина стандартного коэффициента пропорциональна его вкладу в дискриминантную функцию. При этом следует иметь в виду, что если переменные закоррелированы, стандартные коэффициенты не будут отражать действительного вклада.
Количество дискриминантных функций
Задачу дискриминации желательно решать с использованием минимального количества функций. Но количество функций в каждом конкретном случае зависит от конфигурации классов в многомерном пространстве дискриминантных переменных — чем сложнее конфигурация, тем больше функций необходимо для их разделения. Чтобы определить сколько функций необходимо используется проверка функций на значимость. Для характеристики, насколько одна функция слабее другой, используют относительное процентное содержание, которое определяется для одной функции по формуле . Но этот показатель не может служит основанием для отбрасывания части функций. Для оценки значимости используют L-статистику Уилкса. Критериальное значение вычисляется по формуле
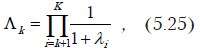
где К — количество классов, а k — число уже вычисленных дискриминантных функций. Чем ближе значение L к нулю, тем лучше различение классов. А чем ближе к 1, тем различение хуже (классы совпадают).
Возможна проверка значимости по критерию c2 с использованием статистики Уилкса. Для этого необходимо рассчитать критериальное значение по формуле

Если это значение больше критического c2 с заданным уровнем значимости и числом степеней свободы (p-k)(K-k-1), то значимость подтверждается.
Классификация при числе групп больше двух
Рассчитанные значения канонической дискриминантной функции fki (см. (5.20) рассматриваются как точки в некотором пространстве. Для каждой группы можно рассчитать центр группирования (среднее). Поэтому в этой новой системе координат для нового объекта рассчитывается расстояние от него до каждой точки группирования. Обычно для этого используется квадрат расстояния Махаланобиса (D2(X,Gk) — расстояние от объекта Х, который необходимо классифицировать, до центра класса Gk). Объект причисляется к группе, расстояние до которой (D2(X,Gk)) наименьшее.
Пошаговый дискриминантный анализ
Позволяет осуществить последовательный отбор дискриминантных переменных, с целью формирования дискриминантных функций с минимальным количеством аргументов при обеспечении надежной классификации.
Вероятность принадлежности к классу
Обычно предполагается равная априорная вероятность принадлежности объекта к определенному классу. Но бывают ситуации, в которых классы по своей природе имеют разное количество элементов. Например, пациенты с некоторыми специфическими особенностями конкретного заболевания составляют только 5% общего количества. В таких ситуациях для правильного решения задачи классификации необходим учет этих вероятностей. Для этого расстояние D2 модифицируют следующим образом:
![]()
где Papriori,k — априорная вероятность принадлежности объекта к группе k.
Классификация без интерпретации
При использовании дискриминантных функций, кроме задачи классификации решается и задача интерпретации. В ряде случаев нет необходимости решать задачу интерпретации. Тогда используют простые классифицирующие функции (в ряде работ именно они называются дискриминантными, а представленные ранее — каноническими дискриминантными функциями), основанные непосредственно на дискриминантных переменных:

где hk — значение функции для k-го класса, xi — значения дискриминантных переменных. Значения bk определяются по формулам

Здесь aij — элемент матрицы, обратной W, которая рассчитывается по (5.22).
Для классификации используется квадрат расстояния Махаланобиса, который вычисляется следующим образом:
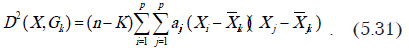
Некоторые авторы [10] рекомендуют использовать скорректированную несмещенную оценку этой величины:
.
Объект Х причисляется к группе, расстояние до которой (D2(X,Gk)) наименьшее. Учет априорной вероятности выполняется по (5.27).
Вероятность принадлежности к классу
В случае, когда имеет место значительное перекрытие классов и, следовательно, слабое их различение, желательно кроме расстояния рассчитывать еще и вероятность принадлежности к классу. Она вычисляется по формуле
,
где fkx — значение дискриминантной функции для объекта Х в k-м классе, fmax — значение дискриминантной функции для объекта Х для класса, расстояние к которому минимальное. Если вероятность мала, то классифицировать объект при данном способе разбиения нельзя.
5.2.2. Набор программ для обработки данных
В связи с отсутствием в Excel средств дискриминантного анализа, предлагаем набор программ, которые вы можете ввести в свою рабочую книгу. Следует иметь в виду, что полноценный дискриминантный анализ требует программ достаточно большого размера и сложности. В связи с этим предлагаем программы для случая двух классов, с ограниченным числом вычисляемых характеристик.
Option Base 1
Sub diskrim_2()
‘Подпрограмма дискриминантного анализа для двух совокупностей
‘объектов
Dim Mean_1() As Double
Dim Mean_2() As Double
Dim Cov_mat_1() As Double
Dim Cov_mat_2() As Double
Dim Cov_all() As Double
Dim Cof_disk()
Dim mat_res()
Dim mas_min() As Double
Dim myfactor_1 As Double
Dim myfactor_2 As Double
‘Ввод ссылки на первую совокупность объектов
Set myCELL1 = Application.InputBox( _
prompt:=»Выберите первую совокупность объектов», _
Type:=8)
‘Ввод ссылки на вторую совокупность объектов
Set myCELL2 = Application.InputBox( _
prompt:=»Выберите вторую совокупность объектов», _
Type:=8)
Set myObj = Application.InputBox( _
prompt:=»Выберите объект, предназначенный для классификации», _
Type:=8)
Set myCell3 = Application.InputBox( _
prompt:=»Выберите ячейку, с которой будут выводиться результаты», _
Type:=8)
Row_1 = myCELL1.Rows.Count ‘Вычисление количества строк
Col_1 = myCELL1.Columns.Count ‘Вычисление количества столбцов
Row_2 = myCELL2.Rows.Count ‘Вычисление количества строк
Col_2 = myCELL2.Columns.Count ‘Вычисление количества столбцов
‘Вычисление векторов средних значений первой и второй
‘совокупностей объектов
ReDim Mean_1(Col_1)
ReDim Mean_2(Col_2)
For i = 1 To Col_1
Mean_1(i) = Application.Average(myCELL1.Columns(i))
Mean_2(i) = Application.Average(myCELL2.Columns(i))
Next i
‘Вычисление ковариационных матриц
ReDim Cov_mat_1(1 To Col_1, 1 To Col_1)
ReDim Cov_mat_2(1 To Col_1, 1 To Col_1)
myfactor_1 = Row_1 / (Row_1 — 1)
myfactor_2 = Row_2 / (Row_2 — 1)
For i = 1 To Col_1
For j = i To Col_1
Cov_mat_1(j, i) = Application.Covar(myCELL1.Columns(j), myCELL1.Columns(i))
‘ MsgBox «Коэффициент ковариации 1 = » & Cov_mat_1(j, i)
Cov_mat_2(j, i) = Application.Covar(myCELL2.Columns(j), myCELL2.Columns(i))
‘ MsgBox «Коэффициент ковариации 2 = » & Cov_mat_2(j, i)
Next j
Next i
‘Получим несмещенную оценку суммарной ковариационной матрицы
ReDim Cov_all(1 To Col_1, 1 To Col_1)
For i = 1 To Col_1
For j = i To Col_1
Cov_all(j, i) = (1 / (Row_1 + Row_2 — 2)) * (Row_1 * Cov_mat_1(j, i) + Row_2 * Cov_mat_2(j, i))
If (i <> j) Then Cov_all(i, j) = Cov_all(j, i)
‘ MsgBox «Коэффициент обобщенной матрицы ковариации = » & Cov_all(j, i)
Next j
Next i
‘Вычисление матрицы, обратной суммарной ковариационной матрице
ReDim Cov_inv(1 To Col_1, 1 To Col_1)
For i = 1 To Col_1
For j = i To Col_1
Cov_inv(j, i) = Application.Index(Application.MInverse(Cov_all()), i, j)
If (i <> j) Then Cov_inv(i, j) = Cov_inv(j, i)
‘MsgBox «Коэффициент обратной матрицы ковариации = » & Cov_inv(j, i)
Next j
Next i
‘Вычислим вектор разницы средних значений
ReDim Aver_all(1 To Col_1, 1 To 1)
For i = 1 To Col_1
Aver_all(i, 1) = Mean_1(i) — Mean_2(i)
Next i
‘Вычисление вектора оценок коэффициентов дискриминации
ReDim Cof_disk(1 To Col_1, 1 To 1)
For i = 1 To Col_1
Cof_disk(i, 1) = Application.Index(Application.MMult(Cov_inv(), Aver_all()), i, 1)
Next i
‘Вычисление оценки дискриминантной функции
Dim U1()
ReDim U1(1 To Row_1, 1 To 1)
ReDim U2(1 To Row_2, 1 To 1)
For i = 1 To Row_1
U1(i, 1) = Application.Index(Application.MMult(myCELL1, Cof_disk()), i, 1)
Next i
For i = 1 To Row_2
U2(i, 1) = Application.Index(Application.MMult(myCELL2, Cof_disk()), i, 1)
Next i
Mid_U2 = Application.Average(U2())
Mid_U1 = Application.Average(U1())
‘ Определим константу
C_const = (Mid_U2 + Mid_U1) / 2
‘Определим возможность отнесения объекта к первой совокупности
U_V = 0
For i = 1 To Col_1
U_V = U_V + myObj.Cells(i) * Cof_disk(i, 1)
Next i
MsgBox «U_V = » & U_V & » C_const = » & C_const
‘Результаты дискриминантного анализа
myCell3.Offset(0, 0).Value = _
«Результаты дискриминантного анализа»
myCell3.Offset(1, 0).Value = _
«Значение константы = »
myCell3.Offset(1, 3).Value = C_const
myCell3.Offset(2, 0).Value = _
«Среднее значение дискриминантной функции = »
myCell3.Offset(2, 5).Value = U_V
If U_V > C_const Then
myCell3.Offset(3, 0).Value = _
«Анализируемый объект принадлежит к 1-й совокупности объектов»
Else
myCell3.Offset(3, 0).Value = _
«Анализируемый объект принадлежит ко 2-й совокупности объектов»
End If
End Sub
5.2.3. Пример
Допустим, у нас есть две выборки больных, к которым применялось одно и то же лечение. Для больных первой группы лечение было успешным, для второй — безрезультатным. Есть все данные по результатам всех проведенных анализов. При поступлении нового больного желательно до начала лечения знать, будет оно успешным или нет.
Рассмотрим процесс решения такой задачи. На рис. 5.16 Х — результаты анализов пациентов, для которых лечение было успешным, а У — результаты анализов пациентов, для которых лечение было неэффективным.
Для выполнения задачи классификации с помощью дискриминантного анализа, выполняем следующие действия. В меню последовательно выбираем Сервис, Макрос. Появляется окно, представленное на рис. 5.6. В этом окне необходимо выбрать discrim_2. Появляется окно, изображенное на рис. 5.12. В нем необходимо дать ссылку на область, в которой находятся данные, характеризующие Х.

После этого запрашивается аналогичная информация о втором объекте У (рис. 5.13).

Затем необходимо указать ячейку, начиная с которой будет выводится результат (рис. 5.14).



Литература, рекомендуемая для изучения
- Алгоритмы и программы восстановления зависимостей / Под ред. В.Н. Вапника. — М.: Наука, 1984.— 816 с.
- Алгоритмы обработки экспериментальных данных.— М.: Наука, 1986.— 184 с.
- Александров В.В., Горский В.Д. Алгоритмы и программы структурного метода обработки данных.— Л.: Наука, 1983.— 208 с.
- Александров В.В., Алексеев А.И., Горский Н.Д. Анализ данных на ЭВМ (на примере системы СИТО).— М.: Финансы и статистика, 1990.— 192 с.
- Дубров А.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. — М.: Финансы и статистика, 1998. — 352с.
- Енюков И.С. Методы, алгоритмы, программы многомерного статистического анализа (пакет ППСА). — (Математическое обеспечение прикладной статистики). — М.: Финансы и статистика, 1986. — 232 с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка. — К.: ЗАО «Укрспецмонтажпроект», 1999. — 312 с.
- Математико-статистический анализ на программируемых микрокалькуляторах / Под ред. В.В. Шуракова. — М.: Финансы и статистика, 1991. — 176с.
- Математическое обеспечение ЕС ЭВМ. — Вып. 14. — Минск: Ин-т математики АН БССР, — 320 с.
- Плюта В. Сравнительный многомерный анализ в эконометрическом моделировании / Пер. с польск. — М.: Финансы и статистика, 1989. — 175 с.
- Прикладная статистика: Классификация и снижение размерности: Справ. изд. / С.А. Айвазян, В.М. Бухштабер, И.С. Енюков, Л.Д. Мешалкин — М.: Финансы и статистика, 1989. — 607 с.
- Райс Дж. Матричные вычисления и математическое обеспечение: Пер. с англ. О.Б. Арушаняна / Под ред. В.В. Воеводина. — М.: Мир, 1984. — 264 с.
- Справочник по прикладной статистике. В 2 т. Т. 2: Пер. с англ.— М.: Финансы и статистика, 1990.— 526 с.
- Статистические методы для ЭВМ / Под ред. К. Энслейна, Э. Релстона, Г.С. Уилфа; Пер. с англ. / Под ред. М.Б. Малютова.— М.: Наука, 1986.— 464 с.
- Факторный, дискриминантный и кластерный анализ: Пер. с англ. — М.: Финансы и статистика, 1989. — 215с.
- Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений / Пер. с англ. Х.Д. Икрамова. — М.: Мир, 1980. — 280 с.