Закономерность и случайность
Содержание
Статистика — совокупность методов, которые дают нам возможность принимать решение в условиях неопределенности.
Абрахам Вальд
2.1. Шкалы измерений
Измеряй все доступное измерению и делай недоступное измерению доступным.
Галилео Галилей
Обработать статистическими методами возможно лишь то, что можно измерить. В связи с этим необходимо рассмотреть существующие шкалы измерений. Измерение — присвоение чисел предметам или событиям, основанное на некоторой системе правил. Для измерения необходимо, чтобы для величин, которые представляют собой результаты измерения изучаемого свойства, выполнялись следующие условия.
Тождество
- Или А = В или А ≠ В
- Если А = В, то В = А
Транзитивность
Если А = В и В = С, то А = С
Ранговый порядок
- Если А > B то B < A
- Если A > B и B > C, то A > C
Аддитивность
- Если А = В и С > 0, то А + С > В
- А + В = В + А
- Если А = В и С = D, то А + С = В + D
- (А + В) + С = А + (В + С)
В зависимости от возможности выполнения этих условий, а также операций над измеренными значениями (“равно”, “не равно”, “больше”, “меньше”, “сложение” и “вычитание”, “умножение” и “деление”), существуют следующие шкалы измерений:
- шкала классификации (наименований);
- шкала порядка;
- шкала интервалов;
- шкала отношений.
Рассмотрим особенности этих шкал.
Шкала классификации (наименования, номинальная). Никакие операции по сравнению, кроме “равны” и “не равны”, невозможны. Нумерация или поименование служит лишь для идентификации объекта — номер дома, номер на майке спортсмена, номер методики лечения и т.п.
Шкала порядка. Возможно сравнение объектов по величине — “больше” или “меньше”. Другие операции невозможны. Примером может служить шкала твердости минералов, содержащая эталонные минералы, выстроенные в ряд, в котором каждый последующий минерал тверже предыдущего. В медицине примером сравнения объектов могут служить: степень тяжести заболевания, “хорошее”, “удовлетворительное” и “плохое” состояние, стадия развития заболевания и пр. Возможны только операции сравнения типа “больше”, “меньше”, “равно”. Значения, выставленные разными специалистами, могут не совпадать (сдвиг шкалы).
Шкала интервалов. В этой шкале возможно не только сравнение по величине, но и определение “насколько больше” (то есть возможны операции “сложения” и “вычитания”). Примером могут служить шкалы измерения температуры (Цельсия, Кельвина, Фаренгейта, Реомюра).
Шкала отношений. В этой шкале возможно выяснение вопроса “во сколько раз” (то есть допустимы все операции: “сравнение”, “сложение” и “вычитание”, “умножение” и “деление”). Пример — вес, длина и пр. В этих случаях существует естественная точка отсчета.
В процессе развития науки и средств измерения возможен переход от одной шкалы измерений к другой, более совершенной. Ведь первые термометры, например, измеряли температуру в шкале порядка (“умерено”, “тепло”, “горячо” и т.п.).
Иногда говорят также о дискретных и непрерывных шкалах измерений. В общем случае к дискретным относятся шкала классификации и шкала порядка. В этих шкалах не существует промежуточных значений их часто называют неколичественными.
Таблица 2.1
Возможные операции в разных шкалах измерений
| Название шкалы | Вид шкалы | Возможные операции |
| Классификации | Дискретная | – ≠ – |
| Порядка | Дискретная | – ≠ > < – |
| Интервальная | Непрерывная | – ≠ > < + – |
| Отношений | Непрерывная | – ≠ > < + – / × |
Шкала измерения, естественно, накладывает ограничения на статистические характеристики, которые могут быть вычислены для случайной переменной, измеренной в конкретной шкале, и на методы обработки, которые корректно можно применять к ним (табл. 2.1, 2.2). В общем случае для обработки данных, измеренных в дискретных шкалах, применяются непараметрические методы.
Таблица 2.2
Статистические характеристики, которые можно вычислить
| Название шкалы | Статистические характеристики, которые можно вычислять |
| Классификации | Частоты, модальный класс |
| Порядка[1] | Частоты, мода, медиана, центили, ранговая корреляция |
| Интервальная | Частоты, мода, медиана, центили, ранговая корреляция, среднее, дисперсия |
| Отношений | Все имеющиеся |
[3] В некоторых работах для таких шкал считают медианное квадратичное отклонение, которое вычисляется аналогично дисперсии, но вместо среднего используется медиана.
В зависимости от вида шкал измерения переменных для исследования связей между ними используют различные статистические методы (см. табл. 2.3).
Таблица 2.3[2]
Связь шкал измерения и применяемых методов
| Шкала измерения влияющих переменных | Шкала измерения зависимых переменных | Применяемые методы |
| Интервалов или отношений | Интервалов или отношений | Регрессионный и корреляционный анализ |
| Время | Интервалов или отношений | Анализ временных рядов |
| Наименований или порядка | Интервалов или отношений | Дисперсионный анализ[3] |
| Смешанный | Интервалов или отношений | Ковариационный и регрессионный анализ |
| Наименования или порядка | Наименования или порядка | Анализ ранговых корреляций и таблиц сопряженности[4] |
| Наименования или порядка | Интервалов или отношений | Дискриминантный анализ
Таксономия Кластерный анализ |
[2] Взято из [4] с незначительными изменениями.
[3] При числе факторов большем двух удобнее пользоваться регрессионным анализом.
[4] Для многоклеточных таблиц сопряженности может быть использован регрессионный анализ.
2.2. Случайные величины
Все, что тебе представляется случайным стечением обстоятельств, вовсе таковым не является.
Станислав Лем, «Собысча»
2.2.1. Общие понятия
При изучении различных дисциплин как в школе, так и в высших учебных заведениях предполагается некая детерминированность, когда каждое событие является следствием другого; а физические законы, например, представляют собой строгие закономерности зависимости одних величин от других. Вместе с тем повседневная деятельность человека постоянно опровергает это положение. Так, при проверке любых физических законов (даже на уровне лабораторных занятий в школе или вузе) обнаруживается, что каждое новое экспериментальное определение величин дает различные результаты. Ведь невозможно, например, точно предсказать количество пассажиров в вагоне метро или в троллейбусе в определенный момент времени и т.д., и т.п. Величины, о которых неизвестно их точное значение для каждой реализации, называются случайными. При этом случайность не означает, что невозможно получить и использовать для практики какую-либо информацию о процессе. Так, при анализе заболеваемости возможно отслеживать тенденции изменения этого показателя на 1000 человек и делать выводы о проведении необходимых мероприятий, планировании требуемого количества лечебных учреждений, медицинского персонала и медикаментов. Несмотря на случайный характер каких-то величин, при их исследовании возможно нахождение определенных закономерностей, которые и используются в практической деятельности.
Для исследования закономерностей, проявляющих себя через случайность, исследуют законы распределения случайных величин и их числовые характеристики.
Вероятность. Это отношение количества благоприятных возможностей к общему их числу (теоретическое классическое определение). Вероятность изменяется от 0 до 1. При этом событие с вероятностью 0 называется невозможным — таким, которое не произойдет ни при каких обстоятельствах. Событие с вероятностью 1 называется достоверным, то есть при данном наборе условий оно будет происходить всегда. Если же вероятность события 0<p<1, то оно может произойти, а может и не произойти. Например, вероятность выпадение четверки на игральной кости равна одной шестой: общее число возможностей шесть (1, 2, 3, 4, 5, 6), а благоприятна из них одна (4). Поскольку в большинстве случаев теоретическое определение невозможно, так как нельзя рассчитать количество общих и благоприятных возможностей, вводится статистическое определение вероятности. По этому определению вероятность равна отношению количества случаев, в которых событие наблюдалось, к общему числу наблюдений. Такая вероятность еще называется относительной частотой. Относительной частотой является понятие заболеваемости, так как представляет собой отношение числа заболевших (больных) к общему количеству. Следует помнить, что относительная частота никогда точно не совпадает с теоретической вероятностью. Например, теоретическая вероятность выпадения “орла” при подбрасывании монеты равна 0,5 (1/2). Если подбрасывать монету и считать относительную частоту, то будет очевидно, что она не совпадает с теоретической вероятностью. Но согласно теореме Бернулли, при достаточно большом числе испытаний вероятность того, что отклонение относительной частоты от теоретической вероятности будет сколь угодно малым, стремится к единице . Из этого следует, что относительная частота обладает свойством устойчивости. Следует иметь в виду, что в данной теореме речь идет о сходимости по вероятности. То есть, с увеличением числа экспериментов к бесконечности разница между относительной частотой и вероятностью необязательно будет сколь угодно мала. Для некоторых n это условие может не выполнятся. Сходимость по вероятности означает, что вероятность такого события очень мала.
Случайной величиной называется величина, которая в результате эксперимента может принять неизвестное заранее значение. Дискретной случайной величиной называется величина, которая принимает отдельные значения (например, количество родившихся детей). Непрерывной является величина, возможные значения которой непрерывно заполняют какой-либо интервал (например, масса тела или рост новорожденных).
Независимые случайные величины. Это такие величины, которые явились результатом независимых случайных событий. То есть таких событий, для которых появление одного события никак не влияет на вероятность появления другого.
2.2.2. Законы распределения случайных величин
Закон распределения — соответствие между значениями случайной величины и вероятностями их реализации. Может быть задан в виде таблицы, формулы или графически.
Для дискретной случайной величины обычно задается рядом распределения (таблица 2.4 — общий вид) или графически в виде многоугольника распределения (см. рис. 2.1).
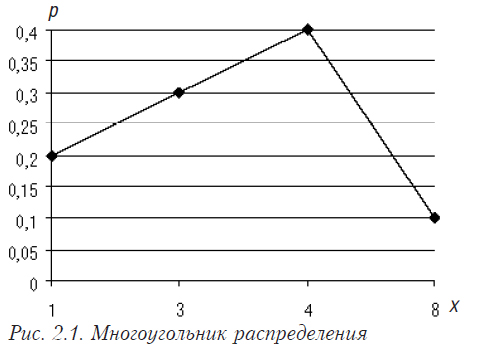
Таблица 2.4
| X | x1 | x2 | … | xn |
| P | p1 | p2 | … | pn |
Рассмотрим конкретный пример.
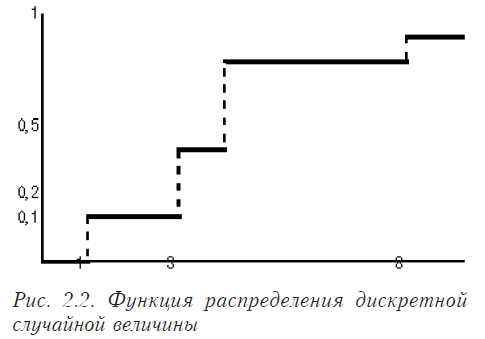
Обратите внимание, что сумма по строке Р должна равняться единице (табл. 2.5). Построим график по данной таблице (см. рис. 2.2):
Таблица 2.5
| X | 1 | 3 | 4 | 8 |
| P | 0,2 | 0,3 | 0,4 | 0,1 |
Для непрерывных табличное задание невозможно, поэтому используются функции распределения.
Функция распределения — это функция F(x), которая задает вероятность того, что случайная величина X в испытании примет значение меньше x:
![]()
Иногда ее еще называют интегральной функцией.
Функция распределения F(x) является неубывающей функцией. То есть если а>b, то F(a) ≥ F(b). При этом F(-∞) = 0 , а F(+∞) = 1. Для дискретных случайных величин функция распределения является разрывной ступенчатой функцией (см. напр. рис. 2.2, на котором приведена функция распределения для распределения, описанного в табл. 2.5).
Вероятность того, что случайная величина попадает в интервал в таком случае определяется по формуле
![]()
Плотность распределения — это
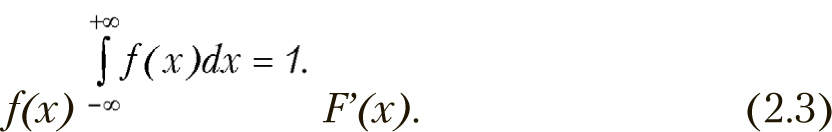
В таком случае вероятность попадания в интервал (a,b) определяется формулой
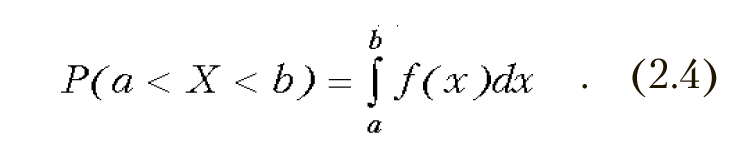
Математическое ожидание
Для дискретной случайной величины определяется по следующей формуле

где xi – значения случайной величины, pi – вероятность появления этих значений. Если бы мы имели в распоряжении генеральную совокупность, то есть все реализации случайной величины, то математическое ожидание было бы равно среднему арифметическому .
Для непрерывных случайных величин формула принимает вид
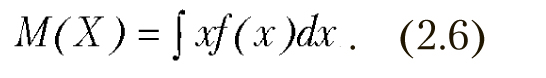
Дисперсия определяется как математическое ожидание квадрата центрированной случайной величины.
![]()
Обычно рассчитывается по формуле
![]()
Среднее квадратичное отклонение определяется следующим образом
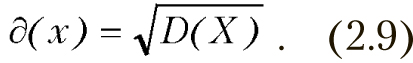
Квантиль — это решение относительно х уравнения
![]()
где р — заданная вероятность. Выделяют следующие частные случаи квантилей, которые имеют собственное название. Например, квартиль — это значение признака, которое делит половину выборки на две равные части (их два). Q1, или нижний квартиль, – это такое значение, для которого выполняется условие, – четверть наблюдений меньше его. Q3 , или верхний квартиль, меньше четверти наблюдений. То есть, медиана и квартили делят ранжированный ряд на четыре равные части. Значение Q3–Q1 называется интерквартильной широтой. Достаточно часто используется величина (Q3–Q1)/2, которая называется семиинтерквартильной широтой. Она является медианой абсолютных отклонений от среднего квартиля (Q3+Q1)/2. Децили, соответственно, такие значения, которые делят ранжированный ряд на 10 равных по объему частей (центили — на сто). Под р-процентным квантилем понимают такое значение признака, которое не превосходит р% наблюдений.
Мы рассмотрим некоторые наиболее важные законы распределения. Из непрерывных к ним относятся нормальный закон распределения (Гаусса) и связанные с ним хи-квадрат, Стьюдента и Фишера, а из дискретных — биномиальное, Пуассона и показательное. Все эти распределения используются в описываемых далее статистических критериях. Для них существуют таблицы (см. приложение).
Нормальный закон распределения (Гаусса)
Для нормального закона распределения плотность распределения имеет следующий вид:
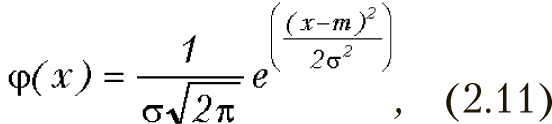
Здесь m — математическое ожидание, а s — дисперсия. Этот закон широко используется в теории вероятности и математической статистике. Стандартным нормальным распределением называется распределение с нулевым математическим ожиданием и единичной дисперсией, плотность которого выглядит следующим образом:
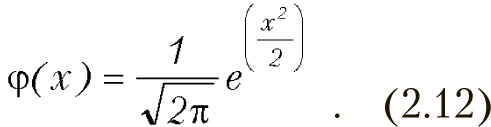
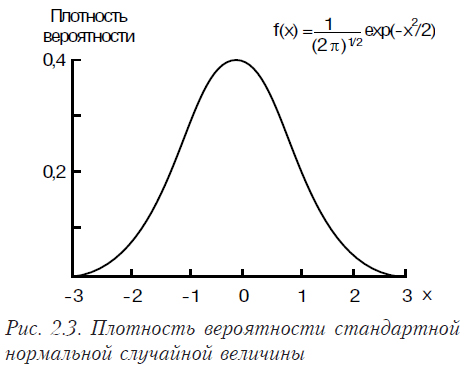
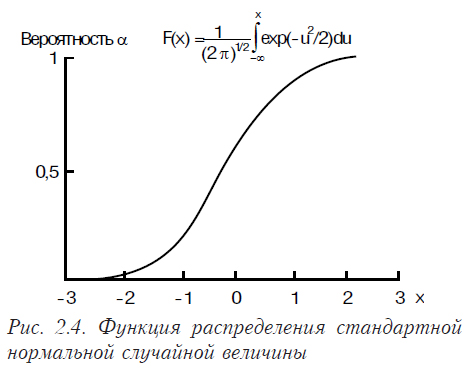
Плотность вероятности стандартного нормального распределения имеет вид представленный на рис. 2.3, функция его распределения представлена на рис. 2.4.
Изменение математического ожидания не изменяет форму кривой, а лишь перемещает ее по оси Х. При изменении дисперсии форма кривой меняется (см. рис. 2.5).
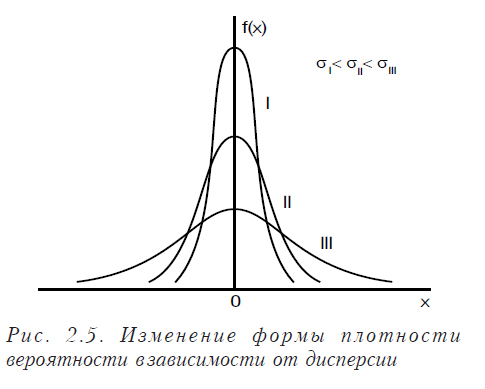
Из рисунка видно, что чем больше дисперсия, тем более пологой и растянутой становится кривая и наоборот.
На нормальном законе распределения базируется практически вся параметрическая статистика. Это связано с тем, что большинство распределений, используемых для проверки статистических гипотез (Фишера, Стьюдента и пр.), являются преобразованиями нормального закона распределения.
Главная особенность нормального закона в том, что он является предельным законом, к которому стремятся при выполнении некоторых законов, все другие законы распределения. Это следует из центральной предельной теоремы (совокупность теорем, относящихся к предельным законам распределения суммы случайных величин). Наиболее важной является теорема Ляпунова, которая гласит: закон распределения суммы независимых случайных величин приближается к нормальному закону при неограниченном росте числа случайных величин и выполнению следующих условий: все величины имеют конечные математические ожидания и дисперсии и ни одна из величин по значению не отличается резко от других.
Распределение Стьюдента
Распределение Стьюдента — это распределение случайной величины
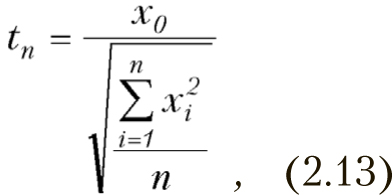
где случайные величины хi имеют стандартное нормальное распределение. Плотность распределения имеет вид
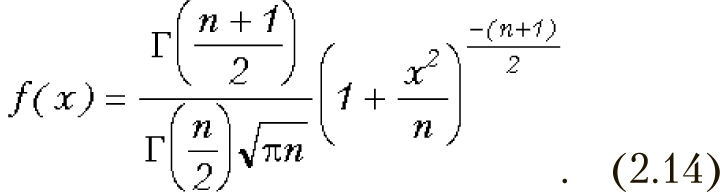
Математическое ожидание распределения Стьюдента равно 0, а дисперсия — n/(n-2). Плотность вероятности и функция распределения Стьюдента с числом степеней 1 представлены на рис. 2.6 и рис. 2.7 соответственно.
Рассмотрим функцию плотности распределения Стьюдента для разных степеней свободы (рис. 2.8).
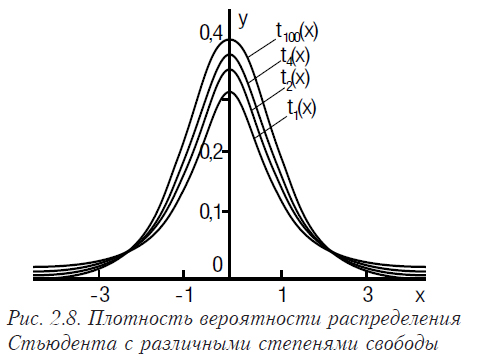
Очевидно, что она очень похожа на плотность нормального распределения.
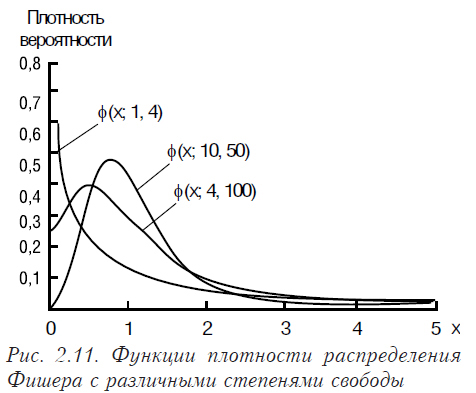
Распределение Фишера
По критерию Фишера распределена случайная величина следующего вида
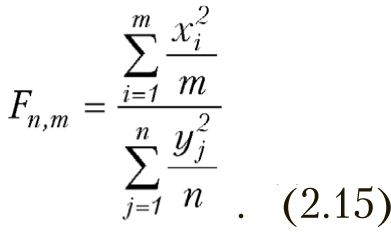
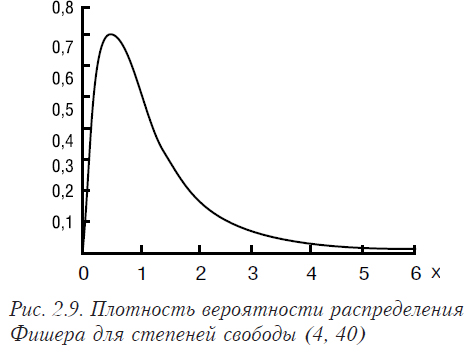
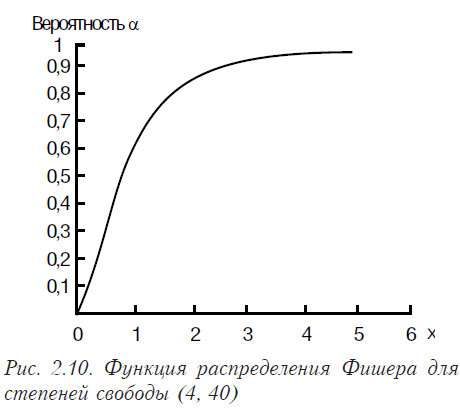
Случайные величины xi и yj распределены по стандартному нормальному распределению. Функции плотности распределения Фишера и соответствующая ей функция распределения представлены на рис. 2.9, 2.10.
На рис. 2.11 показаны функции плотности распределения Фишера с различными степенями свободы.
Распределение хи-квадрат Пирсона
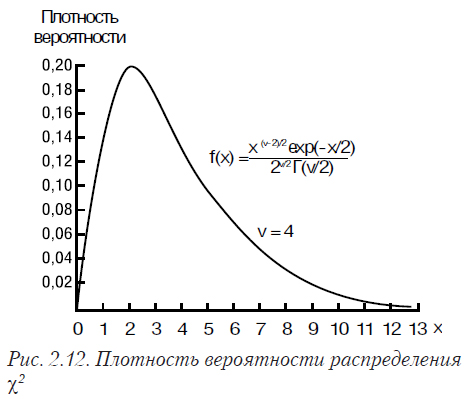
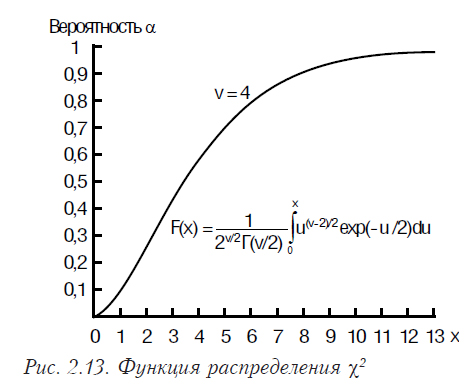
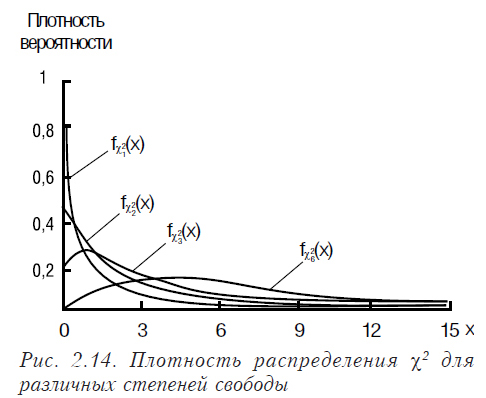
Распределение χ2 имеет случайная величина, представляющая собой сумму квадратов случайных величин, каждая из которых распределена по нормальному закону. Плотность распределения χ2 имеет вид (2.16), где Г() — гамма-функция. Математическое ожидание распределения χ2 равно n, а дисперсия 2n. Графики функций плотности вероятности и функции распределения χ2 приведены на рис. 2.12, 2.13.
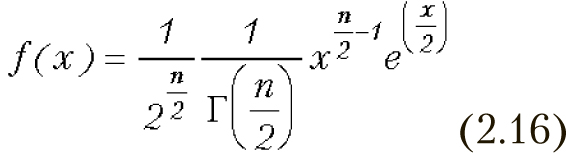
Как отличаются плотности распределения этой функции для различных степеней свободы демонстрирует рис. 2.14.
Биномиальное распределение
Это распределение вероятностей появления m событий в n независимых испытаниях, при постоянной вероятности события в каждом испытании р. Вероятность возможного числа событий определяется по формуле Бернулли.
![]()
где p — вероятность появления события в каждом испытании, m — ожидаемое число событий, n — общее число испытаний, q=1–p , (2.18).
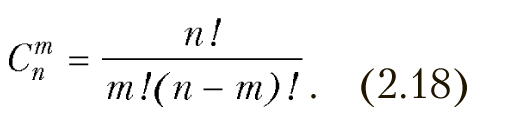
Биномиальное распределение может быть задано в виде ряда, представленного в табл. 2.6.
Таблица 2.6
| X=m | 0 | 1 | … | k | … | n |
| Pn(m) | qn | p1qn-1 | … | … | pn |
Математическое ожидание биномиального распределения равно np, а дисперсия — npq. При большом количестве испытаний биномиальное распределение становится весьма близким к нормальному (рисунок 2.15). Этот факт доказывается в локальной теореме Муавра-Лапласа (относящейся предельным теоремам). Из нее следует, что при большом n вероятность того, что в n испытаниях событие наступит m раз можно определить по формуле:
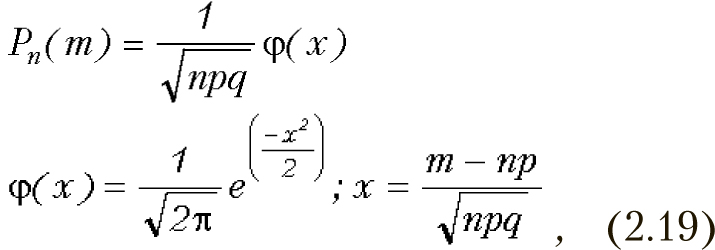
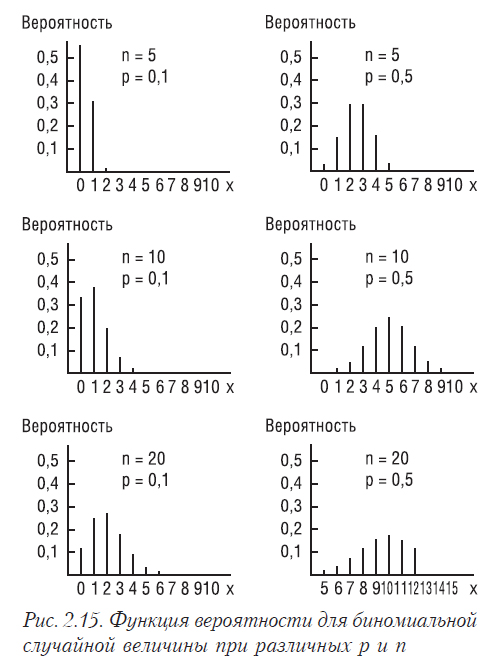
Хорошо видно, что форма распределения с ростом n приближается к нормальной, но тем медленнее, чем меньше р.
Распределение Пуассона (закон распределения редких событий)
В том случае, когда p или q мало при росте числа испытаний биномиальное распределение стремится к распределению Пуассона, которое задается формулой
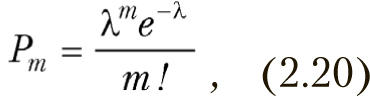
где λ=np — интенсивность. Она считается постоянной, не зависящей от числа n. И дисперсия и математическое ожидание в распределении Пуассона равны np=λ.
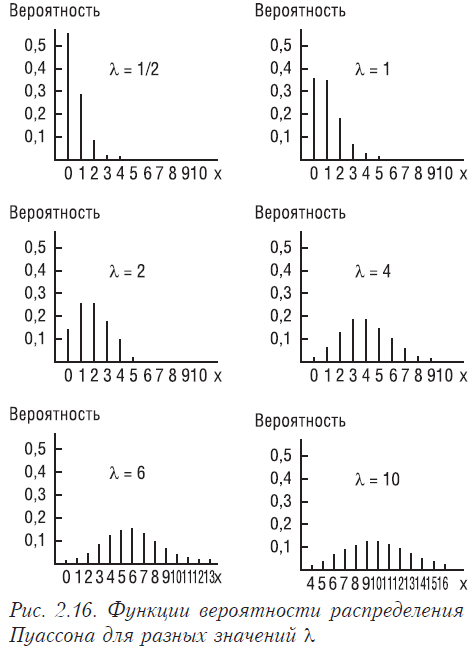
Пуассоновское распределение широко используется при моделировании систем массового обслуживания (телефонные станции, торговые и банковые учреждения и пр.). Рассмотрим функции вероятности распределения Пуассона для разных значений λ на рис. 2.16.
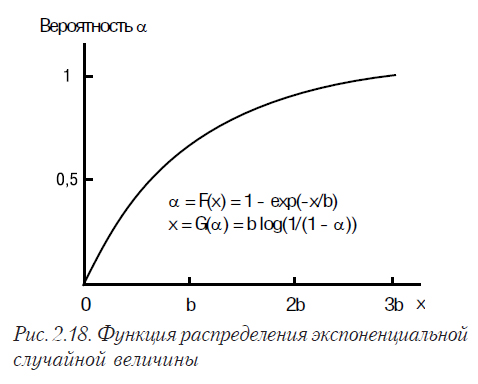
Показательное распределение (экспоненциальное)
Очень многие случайные величины распределены по экспоненциальному закону (например, интервалы между вызовами “скорой помощи”, объемы реализации наиболее продаваемых препаратов, доли рынка различных компаний и пр.).
Плотность распределения для показательного распределения имеет вид:
![]()
Функция распределения для показательного распределения имеет вид:
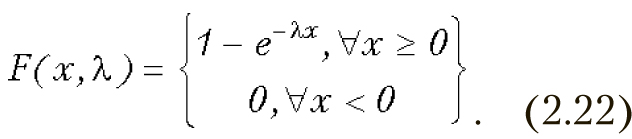
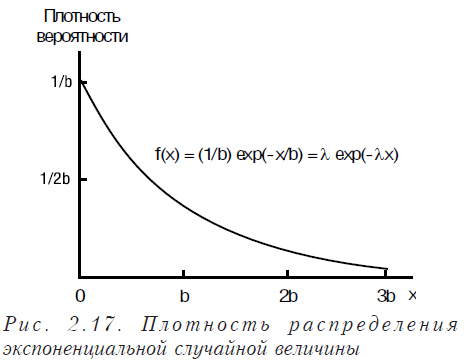
Математическое ожидание для показательного закона распределения равна 1/λ , а дисперсия — 1/λ2. На рис. 2.17 и 2.18 показаны плотность распределения и функция распределения экспоненциальной случайной величины.
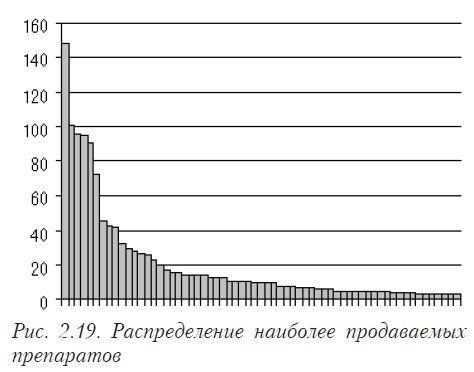
На рис. 2.19 показано распределение объема реализации наиболее продаваемых препаратов в Украине (1997 г.). Очень похожую форму имеет распределение заболеваемости по областям Украины и многие другие случайные величины.
В большинстве случаев при решении реальных задач закон распределения и его параметры неизвестны. Поэтому для определения вида закона распределения и его параметров необходимо выполнять ряд действий по анализу полученных исходных данных.
2.2.3. Выборочный метод
Как правило, в реальных исследованиях мы не имеем генеральной совокупности значений изучаемой величины (т.е. всех возможных значений). Нам приходится использовать для работы некоторую выборку из нее.
Теорема Чебышева. На выводах из теоремы Чебышева основывается выборочный метод. Теорема гласит: Если Х1, Х2, Х3, ….Хn — попарно независимые случайные величины, при этом дисперсии их равномерно ограничены (т.е. не превышают некоторое постоянное значение), то для сколь угодно малого наперед заданного числа e вероятность выполнения условия будет сколь угодно близка к 1 при достаточно большом числе случайных величин n.
Иначе:
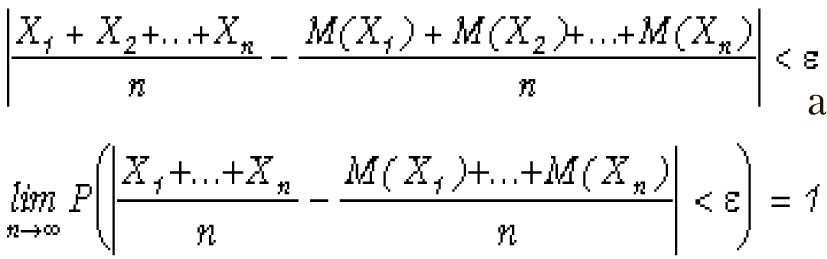
Для частного случая, когда все независимые случайные величины имеют одно и то же математическое ожидание М указанное выражение принимает следующий вид:
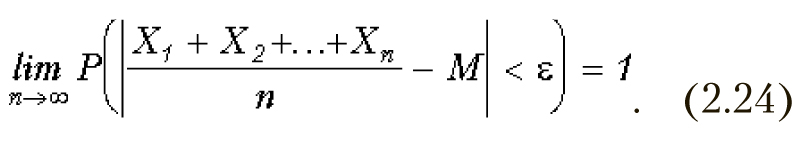
Сущность теоремы Чебышева состоит в том, что среднее арифметическое большого количества независимых случайных величин, дисперсии которых равномерно ограничены, утрачивает случайный характер и по вероятности сходится к математическому ожиданию[5].
Выводами из теоремы Чебышева широко пользуются на практике, считая, что при увеличении числа измерений величины, точность ее определения возрастает. К сожалению, при этом забывают, что в ней сформулированы условия, при которых это явление будет иметь место, а именно:
- попарная независимость случайных величин (экспериментов);
- дисперсии равномерно ограничены;
- одно и то же математическое ожидание.
Теорема Чебышева, теорема Бернулли и неравенство Чебышева часто называются законом больших чисел.
[5] Смотри выше объяснение о сходимости по вероятности: это совсем не значит, что среднее становится равным математическому ожиданию.
Гистограмма
Служит для изображения интервального ряда: по оси абсцисс откладывают интервалы и на этих отрезках строят прямоугольники с высотой, равной частоте (количеству реализаций) или частости (доли реализаций от общего количества) соответствующего интервала (табл. 2.7 и рис. 2.20).
Таблица 2.7
Наблюдаемые частоты случайной величины
| Интервал изменения случайной величины |
Частота реализаций величины, попадающей в этот интервал |
| 0—12 | 4 |
| 12—24 | 14 |
| 24—36 | 32 |
| 36—48 | 48 |
| 48—60 | 44 |
| 60—72 | 33 |
| 72—84 | 15 |
| 84—96 | 5 |
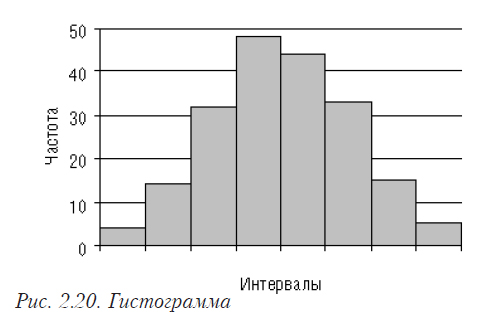
Если установить по оси Х ширину интервала равную 1, а по оси У — ширину интервала равную одному наблюдению, то площадь гистограммы будет равна числу наблюдений для частот или 1 для частостей.
Полигон частот
Аналог гистограммы для дискретного распределения. По оси абсцисс откладываются значения величин, а по оси ординат — частоты или частости. Полученные точки соединяются ломаной. Может быть построен для непрерывного распределения, тогда ломаной соединяются середины верхних отрезков прямоугольников гистограммы (рис. 2.21).
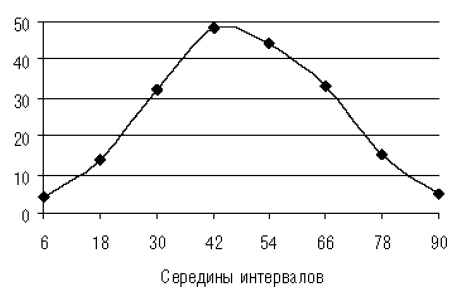
Рис. 2.21. Полигон частот для непрерывного распределения
При построении гистограмм важное значение имеет выбор интервалов — форма распределения будет зависеть от этого выбора. Существуют формулы расчета размера интервала, но обычно считается, что интервалов должно быть 12–15, при этом в каждый интервал должно попасть не менее 5–6 реализаций величины (интервалы в общем случае могут быть разной величины).
Кумулятивная кривая
По оси абсцисс откладываются интервалы, а по оси ординат — число или доля элементов совокупности, имеющие меньшее или равное заданному числу значение. На рис. 2.22 показана кумулятивная кривая для выборки, которая представлена на гистограмме рис. 2.20.
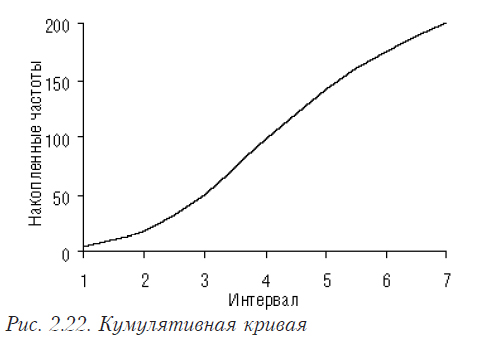
Как видно, при увеличении до бесконечности размера выборки гистограмма превращается в график плотности распределения, а кумулятивная кривая — в график функции распределения.
Об определении закона распределения случайной величины
В классической математической статистике много внимания уделяется определению вида и параметров закона распределения случайной величины. Для проверки соответствующих гипотез существуют различные критерии и программное обеспечение. В практических исследованиях эта задача требует немалые усилия, и ее разрешение проблематично по многим причинам: разные критерии дают разный результат; изменение разбиения на интервалы может изменить выводы; эмпирическое распределение может быть смесью различных распределений или “засоренным” по сравнению с теоретическим и пр. Для экспериментатора необходимость заниматься этим вопросом существует в следующих случаях:
- применяемые им методы в качестве предпосылок требуют определенного закона распределения;
- решаемая задача (например, имитационное моделирование) требует знания вида и параметров закона распределения.
В первом случае ограничиваются обычно нестрогими простыми проверками, достаточными для принятия решения, или выбирают непараметрические методы, не требующие знания закона распределения. Во втором — аппроксимируют эмпирический закон распределения функциями Пирсона.
Можно считать, что случайная величина распределена по нормальному закону, если выполняются нижеприведенные условия, являющиеся следствием из нормального закона распределения. Для проверки находят среднее абсолютное отклонение
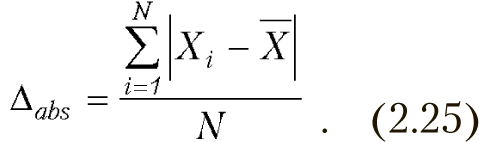
Затем проверяют выполнение следующих условий.
- Количество положительных и отрицательных отклонений от среднего — приблизительно равны.
- Половина (или чуть больше) отклонений от среднего по абсолютной величине меньше среднего абсолютного отклонения εi<Δabs.
- Ни одно из отклонений не превышает среднее абсолютное отклонение больше чем в 3…4 раза: εimax< 3 … 4 Δabs.
Предлагаются и другие возможные проверки. Например, достаточно проверить выполнение следующего условия:
Для тех, кто не хочет вычислять среднее абсолютное отклонение, можно проверить выполнение следующего комплекса условий.
- Почти все (99,7%) отклонения от среднего меньше 3 сигм: εi< 3σ.
- Две третьи (68,3%) отклонений меньше, чем σ.
- Половина отклонений меньше, чем 0,625σ.
Если все эти условия выполняются, то можно считать, что гипотеза о нормальном распределении не противоречит имеющимся данным.
Во многих источниках имеются рекомендации по действиям, которые необходимо предпринять, чтобы распределение стало нормальным:
- функциональные преобразования;
- цензурирования выборки.
В качестве преобразований обычно предлагается вычисление логарифмов, арксинуса, квадратного и кубических корней от исходных величин. При использовании этих преобразований следует помнить:.
- Преобразованная величина должна иметь естественный смысл. Например, если оцениваемые значения различаются в десятки раз, использование логарифмирования (или преобразование вида квадратного корня для величин, являющихся площадями) интуитивно представляется естественным.
- Выводы, которые вы будете делать на основании последующего анализа, относятся не к исходным величинам, а к их функциям.
При цензурировании обычно отбрасывают наибольшие и наименьшие значения. Следует иметь в виду, что при этом происходит «выхолащивание» исходной задачи, ее идеализация. По современным представлениям широко распространены нормальные распределения с «тяжелыми хвостами», для которых, в отличие от стандартного нормального распределения, частота появления минимальных и максимальных значений достаточно высока.
Необходимо помнить, что статистика базируется на выборочном методе, когда изучается не вся генеральная совокупность, а лишь некоторая выборка из нее. Справедливость и обоснованность такого подхода базируется на ряде теорем. Одной из наиболее важных из них является теорема Чебышева. В ней сформулированы условия, которые должны выполняться для ее использования:
- попарная независимость случайных величин;
- одинаковое математическое ожидание в этих случайных величинах;
- равномерная ограниченность дисперсий этих случайных величин.
При невыполнении хотя бы из одного из перечисленных условий выводы будут неправомерны!
2.3. Характеристики случайной величины
Средний человек в обществе то же, что центр тяжести в физическом теле;
имея в виду эту центральную точку, мы приходим к пониманию всех явлений равновесия и движения.
Адольф Кетле
В статистике при анализе данных приходится сталкиваться со следующими проблемами:
- Сколько данных необходимо выбрать и как их отбирать.
- Правомочность распространения выводов, сделанных на основании выборочных данных на всю генеральную совокупность.
- Выбор оптимальных способов оценивания.
- Выбор способов обобщения, классификации и представления данных.
Исследователь всегда должен помнить об этих проблемах, поскольку он отвечает за результаты исследований и сделанные выводы, которые могут повлиять на благосостояние, здоровье и жизнь многих людей.
2.3.1. Свойства оценок параметров
Оценки параметров должны отвечать нижеперечисленным требованиям[6]:
Несмещенность. Это означает, что при проведении очень большого количества испытаний с выборками одинакового размера среднее значение каждой выборки стремится к истинному значению генеральной совокупности. Смещенность обычно обусловлена наличием систематической ошибки.
Состоятельность. С ростом размера выборки оценка должна стремится к значению соответствующего параметра генеральной совокупности с вероятностью, стремящейся к 1.
Эффективность. Выбранная оценка для выборки равного объема должна иметь минимальную дисперсию.
Достаточность. Оценка должна содержать всю необходимую информацию и не требовать дополнительной.
При разработке оценок обычно выдвигают некоторые предпосылки. Поэтому оценки, как правило, отвечают приведенным требованиям только при выполнении этих предпосылок. Об этом следует помнить при использовании оценок.
Для оценивания параметров используются различные методы, особое место среди них занимает метод максимального правдоподобия. Он применяется в тех случаях, когда известен закон распределения. Суть его в том, что оценки должны быть равны значениям, при которых выборка имеет максимальную вероятность появления.
К характеристикам одномерного распределения относятся:
- Меры положения (среднее, медиана, мода и др.).
- Меры рассеивания (размах, коэффициент вариации, дисперсия, среднеквадратичное отклонение).
- Меры формы (асимметрия, эксцесс, моменты третьего и четвертого порядка).
[6] Названия состоятельная (consistent), эффективная (efficient) и достаточная (sufficient) оценка введены Р.А. Фишером в 1925 г. В настоящее время, как правило, принимаются во внимание первые три свойства.
2.3.2. Среднее арифметическое (выборочное)
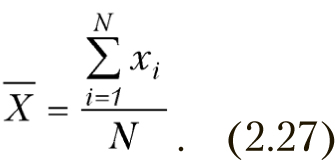
Свойства среднего (выборочного)
- Сумма отклонений от среднего равна 0.
- Если все значения выборки увеличить или уменьшить, умножить или разделить на одно и то же число, то среднее значение изменится аналогично.
- С увеличением числа измерений точность оценки растет и среднее приближается к математическому ожиданию, но только в том случае, если нет систематических ошибок и наблюдения независимы.
- Среднее суммы двух выборок равно сумме их средних, если выборки одинаковых размеров (аналогично для разности):
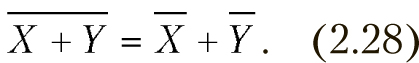
- Если ряд наблюдений состоит из К групп, то среднее арифметическое всего ряда равно взвешенной групповой средней, весами при этом являются объемы групп[7]:
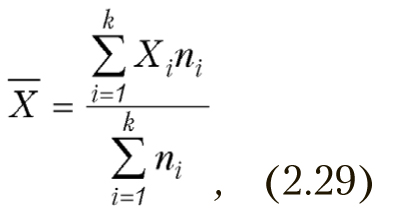
где ni – размер i-ой группы,
Хi – среднее i-ой группы.
Несколько обескураживающих замечаний
- Среднее вовсе не означает типичное. Например, средний доход вовсе не является типичным.
- Среднее не совпадает с математическим ожиданием. За исключением случая нормального распределения арифметическое среднее даже не является несмещенной оценкой математического ожидания с наименьшей дисперсией. Более того, даже для нормального распределения можно указать оценку, которая будет ближе к математическому ожиданию (правда, без некоторых полезных свойств среднего) [12].
[7] Такую формулу обычно используют в тех случаях, когда мы имеем сгруппированные данные, например, интервалы доходов (от и до) и доля населения, имеющего доходы. Тогда середина интервала считается средним и мы можем выполнять расчет среднего для всей выборки.
2.3.3. Среднее геометрическое (выборочное)
Геометрическое среднее применяется если:
- переменная изменяется во времени с постоянным соотношением между ее измерениями (например, рост числа бактерий, рост капитала на счету, эксплуатационные расходы и пр.);
- отдельные значения в выборке отстоят очень далеко друг от друга (например, разница на порядок между значениями).
Геометрическое среднее рассчитывается по формуле
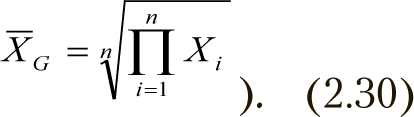
2.3.4. Среднее гармоническое
В ряде случаев (например, расчет средней продолжительности жизни, определение средней скорости при движении с различными скоростями и др.) используется гармоническое среднее
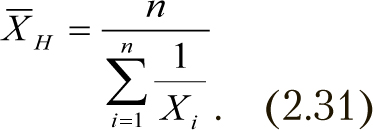
2.3.5. Мода
Это значение, которое наблюдается наибольшее число раз (наиболее вероятная величина).
Для интервального вариационного ряда рассчитывается по формуле:
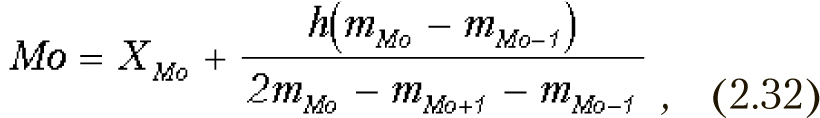
где XMo — начало модального интервала (то есть такого, которому соответствует наибольшая частота);
h — величина модального интервала;
mMo — частота модального интервала;
mMo-1 — частота интервала, предшествующего модальному;
mMo+1 — частота интервала, следующего за модальным.
Помните, что мода не применима в том случае, если распределение мультимодальное (многовершинное).
2.3.6. Медиана (выборочная)
Медиана — это значение, которое делит ранжированный вариационный ряд на две равные по объему группы. Вариационный ряд ранжируется. Если количество членов ряда нечетное, медианой является значение ряда, которое расположено посредине, т.е., элемент с номером (N+1)/2. Если число членов ряда четное, то медиана равна среднему членов ряда с номерами N/2 и N/2+1. Например, для ряда 4; 5; 6,7; 8; 12 медианой будет значение 6,7. Для интервального вариационного ряда медиана вычисляется по формуле:
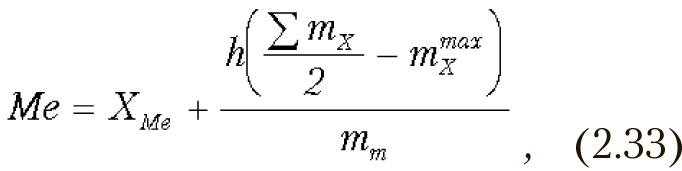
где XMe — начало медианного интервала;
h — величина медианного интервала;
mX — частоты по всем интервалам;
mmaxX — частота, накопленная к началу медианного интервала;
mm — частота медианного интервала.
Медианным называется интервал, в котором находится значение медианы.
Свойства медианы
- Сумма абсолютных величин отклонений вариантов от медианы, умноженных на соответствующие частоты, меньше, чем от любой другой величины[8]:
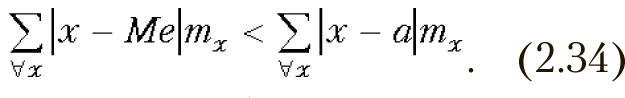
- На значение медианы не влияет изменение крайних значений вариационного ряда, если только меньшее медианы остается меньшим, а большее продолжает оставаться больше ее[9].
[8] Это свойство медианы может использоваться, например, для выбора местоположения остановки городского транспорта, бензоколонок и т.п.
[9] В связи с этим свойством, медиану используют вместо среднего в том случае, если крайние значения вариационного ряда резко отличаются от остальных.
2.3.8. Показатели вариации
Вариационный размах
![]()
Ненадежен, поскольку на него влияют крайние значения. Не изменяется при любых изменениях вариационного ряда, не затрагивающих крайние значения.
Эмпирическая дисперсия
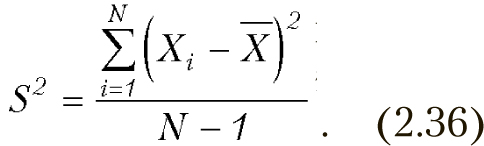
Свойства дисперсии
- Дисперсия постоянной величины равна 0.
- Если все результаты увеличить или уменьшить на одно и то же число, то дисперсия не изменится.
- Если все результаты изменить в К раз то дисперсия изменится в К2 раз[10].

Корень квадратный из дисперсии представляет среднеквадратическое отклонение — S. В англоязычной литературе этот термин принято называть стандартной ошибкой среднего.
Некоторые замечание к вопросу о N или N-1
Один из наиболее часто встречающихся вопросов: на что делить сумму квадратов в формуле дисперсии, на N или N-1?
В общем случае различие между этими оценками невелико, но все же может иметь значение в том случае, когда математическое ожидание известно, несмещенной оценкой дисперсии является
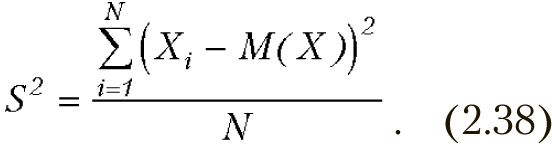
Но сумма квадратов в числителе формулы минимальна только в случае, если математическое ожидание равно среднему, что вовсе не так. Поэтому необходима поправка Бесселя, которая приводит к появлению в знаменателе N-1.
На практике часто поступают следующим образом. Если математическое ожидание известно или оценка его получена по другой выборке — используют формулу с N. В том случае, когда оценка среднего получена по той же выборке, по которой оценивается дисперсия, то используют N-1.
Коэффициент вариации
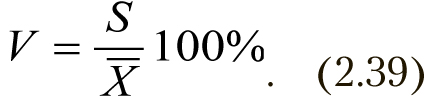
В том случае, если полигон частот вариационного ряда не имеет значительной скошенности, а все члены ряда положительны, то V < 30%. Если коэффициент вариации больше 100%, то это обычно означает, что данные неоднородны.
[10] Тот факт, что в период инфляции бедные становятся беднее, а богатые — богаче, с точки зрения статистики является всего лишь свойством дисперсии.
2.3.9. Доверительный интервал
Доверительный интервал — интервал, относительно которого с наперед заданной вероятностью P = 1 – α можно утверждать, что он содержит неизвестное значение параметра q.
![]()
где 1 – α — доверительная вероятность,
α — уровень значимости.
Свойства
- при росте числа измерений точность повышается. Это справедливо только в том случае, если нет систематических ошибок и наблюдения независимы;
- увеличение надежности при фиксированной выборке ведет к увеличению доверительного интервала и снижению точности.
Если мы увеличиваем количество измерений, то оценка параметра становится более точной и доверительный интервал уменьшается. Это не относится к тем ситуациям, когда измерения зависимы или в них присутствуют систематические ошибки. В этих случаях точность при увеличении количества измерений не только не увеличивается, но может даже снижаться. Рассмотрим в качестве иллюстрации простой пример.
Известно, что усреднение времени, показываемого часами большого количества случайно взятых людей, дает достаточно хорошую оценку точного времени. Допустим, что в выборке, по которой мы выполняем усреднение, большинство людей непосредственно перед проверкой выставили время на своих часах в соответствии с часами одного из участников опроса. В этом случае измерения не будут независимыми, и среднее сместится. Вследствие чего рассчитанное значение доверительного интервала не будет соответствовать действительности. Если аналогичный опрос провести на границе суток, в которых происходит смена летнего и зимнего времени, то в этих измерениях будет присутствовать систематическая ошибка, связанная с тем, что у значительной части людей часы не будут переведены.
Приведем пример несоответствия доверительного интервала фактическому значению. Измерения размеров Земли выполнялись с помощью наземных средств (с развитием научно-технического прогресса — со все большей точностью). Но, когда измерения были сделаны с помощью искусственных спутников Земли, то оказалось, что эти размеры находятся вне пределов рассчитанных доверительных интервалов: в методиках расчета были систематические ошибки, которые не могли быть устранены увеличением количества измерений.
Доверительный интервал означает не вероятность попадания значения оцениваемого параметра в пределы определенных границ, а то, что если мы возьмем достаточное число выборок, 100% случаев параметр будет находиться в заданном интервале.
Уровень значимости выбирается обычно в интервале от 0,01 до 0,05. При этом 0,05 — обычные требования надежности, 0,01 — повышенные, 0,001 — очень высокие, 0,1 — пониженные.
Доверительный интервал для среднего
Определяется по формуле:
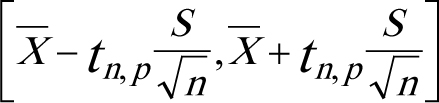
где S — среднее квадратическое отклонение,
n — число опытов,
tn, p — табличное значение распределения Стьюдента с числом степеней свободы n и доверительной вероятностью p.
Эту формулу применяют в тех случаях, когда дисперсия неизвестна и используют ее оценку по экспериментальным данным. Если дисперсия известна, применяют другую формулу (здесь не приводится, так как вероятность возникновения подобной ситуации крайне мала).
Доверительный интервал для среднего квадратического отклонения
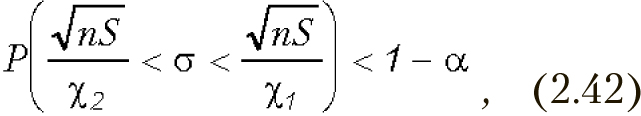
где χ1 и χ2 — квантили распределения χ2 (хи-квадрат).
Квантили χ1 и χ2 имеют по (n–1) степеней свободы и уровень значимости 1 – α/2 и α/2 соответственно.
Примечание:
- В тех случаях, когда по одной выборке определяются несколько параметров, доверительные интервалы будут больше, чем ожидаемые. Это связано с тем, что статистики, используемые для построения доверительных интервалов параметров (например, среднего и дисперсии) не являются независимыми.
- Приведенные формулы для доверительных интервалов получены исходя из нормального распределения данных.
2.3.10. Понятие о параметрической, непараметрической и робастной статистике
Известно, что для проверки любой гипотезы, необходимо опираться на некую совокупность предположений, из которых и выводятся формулы, необходимые для этой проверки. При этом среди прочих всегда присутствуют предположения о законе распределения выборки. Понятно, что невыполнение этих предпосылок делает некорректным применение соответствующих методов.
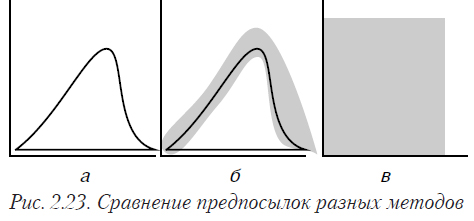
Параметрические методы предполагают конкретное распределение с определенными параметрами (рис. 2.23а). Практически все традиционные статистические критерии и методы относятся к этой группе. Они обычно строго обоснованы и хорошо изучены. Проблема в том, что в подавляющем большинстве практических задач предпосылки нормальности не выполняются (или проверить их выполнение невозможно).
Робастные методы также предполагают конкретное распределение, но допускают отклонения от него (рис. 2.23б). Форма и величина этих отклонений зависят от конкретного метода. Не для всех видов задач имеются разработанные робастные методы.
Непараметрические методы не делают конкретных предположений о законе распределения — только самые общие (рис. 2.23в). Например, выборка имеет непрерывный закон распределения, или обе выборки имеют один закон распределения и пр. Обычно достаточно строго обоснованы. Для многих задач, особенно многомерных, не существует соответствующих непараметрических методов.
Анализ данных обычно представляют собой некоторые эвристические процедуры, разработанные для решения конкретного класса задач. Обоснованность их опирается лишь на логику и проведенный вычислительный эксперимент со специально сформированными искусственными наборами данных.
Выбор методов осуществляется в зависимости от цели исследования и особенностей имеющихся данных.
2.4. Примеры расчетов и построений
Ученость сама по себе дает указание чересчур общие, если их не уточнить опытом
Френсис Бэкон
2.4.1. Вычисление среднего и медианы, сравнение их устойчивости
Рассмотрим пример вычисления среднего значения и медианы.
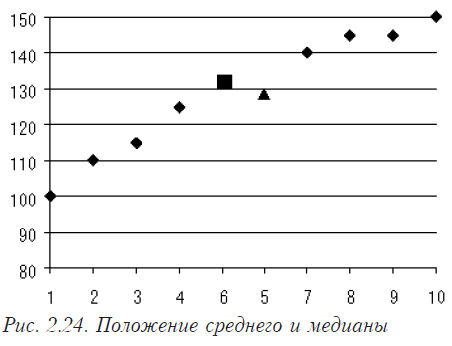
Таблица 2.8 содержит цены на некоторый препарат в различных торгующих организациях.
Таблица 2.8
| Организация | А | Б | В | Г | Д | Е | Є | Ж |
| Цена | 100 | 110 | 115 | 125 | 140 | 145 | 145 | 150 |
Среднее значения цены = (100+110+115+125+140+145+145+150)/8 =128,75
Ранжированный ряд = {100;110;115;125;140;145;145;150}
Медиана цены = (125+140)/2 = 132,5 (число членов ряда четное)
На рис. 2.24 показано положение среднего (квадрат) и медианы (треугольник) в ряду данных.
Допустим, что у нас есть выделяющиеся данные (см. табл. 2.8).
Таблица 2.9
| Организация | А | Б | В | Г | Д | Е | Є | Ж | З |
| Цена | 100 | 110 | 115 | 125 | 140 | 145 | 145 | 150 | 450 |
Среднее значение цены = (100+110+115+125+140+145+145+150+230)/9=164,4
Ранжированный ряд = {100;110;115;125;140;145;145;150;230}
Медиана цены = 140 (число членов ряда нечетное)
На рис. 2.25 отображено положение среднего (квадрат) и медиан (треугольник) в ряду данных.
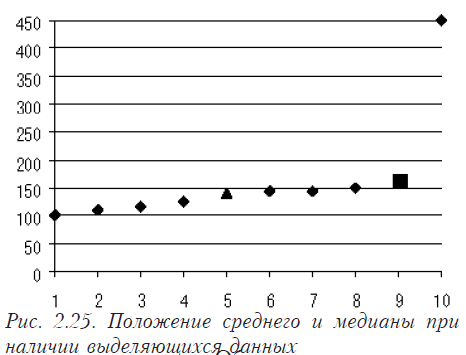
Этот пример демонстрирует, что при наличии данных, которые резко выделяются или заметно отличаются друг от друга, медиана является более стойкой оценкой, чем среднее значение.
2.4.2. Расчет среднего, моды и медианы для сгруппированных данных
Такая задача является типичной в задачах медицинской статистики и маркетинга.
Допустим, имеется таблица 2.10, для которой необходимо рассчитать среднее, моду и медиану для возраста заболевших.
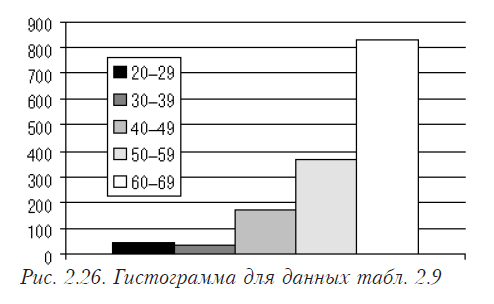
Гистограмма для этих данных представлена на рис. 2.26.
Таблица 2.10
| Возраст | 20–29 | 30–39 | 40–49 | 50–59 | 60–69 |
| Число заболевших | 45 | 36 | 175 | 361 | 825 |
| Накопленные частоты | 45 | 81 | 256 | 617 | 1442 |
Среднее значение возраста заболевшего:
Хсреднее = (24,5*45+34,5*36+44,5*175+54,5*361+64,5*825)/(45+36+175+361+825) =58,57
Медиана вычисляется по формуле 2.33.
XMe = 60 — начало интервала, который содержит медиану. Поскольку сумма частот 1442, то половина (медиана делит пополам) — 721. К началу интервала 60–69 накоплено только 617, поэтому ясно, что медиана находится именно в этом интервале.
h = 69–59 — ширина медианного интервала. Вычитается 59, так как 60 является частью интервала.
mX /2 =1442/2 — общая накопленная частота делится на 2.
mmaxX=617 — частота, накопленная к началу медианного интервала.
mm=825 — частота медианного интервала.
Таким образом медиана будет равна:
Хmе=60+10*(1442/2-617)/825=61,26.
Мода вычисляется по формуле 2.32.
Xmo = 60 — начало модального интервала. Модальным является тот интервал, в котором частота наибольшая.
h = 69–59 — ширина модального интервала.
MMo = 825 — частота модального интервала.
mMo-1 = 361 — частота интервала, который предшествует модальному.
mMo+1 = 0 — поскольку это частота интервала, следующего за модальным, а модальный интервал является последним.
Мода будет равна:
ХMо = 60+10*(825-361)/(2*825-0-361) = 65.
2.4.3. Расчет показателей вариации
Рассмотрим следующую таблицу, для данных которой рассчитаем показатели вариациий.
Вариационный размах R = 91,2 – 70,1=21,1
Среднее = 76,32
Дисперсия S2 = ((75,7–76,32)2 + (70,1–76,32)2 + (91,2–76,32)2 + (70,7–76,32)2 + (71,4–76,32)2 + (78,8–76,32)2)/(6–1) = ((-0,62)2 + (-6,22)2 + (14,88)2+(-5,62)2 + (-4,92)2+(2,48)2)/6 =(0,3844 + 38,6884 + 221,4144 + 31,5844 + 24,2064 +6,1504)/5 = 64,13
Среднеквадратическое отклонение — 8,008
Коэффициент вариации — V = (8,008/76,32)
100% = 10,49%
2.4.4. Расчет доверительных интервалов
Используя данные таблицы 2.11 и рассчитанные значения среднего и среднеквадратичного отклонения, построим для них доверительные интервалы.
Таблица 2.11
| Больной | А | Б | В | Г | Д | Е |
| Содержание гемоглобина в крови, мкмоль | 75,7 | 70,1 | 91,2 | 70,7 | 71,4 | 78,8 |
Доверительный интервал для среднего:
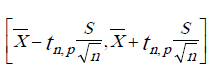
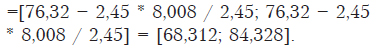
2,45 в числителе — табличное значение критерия Стьюдента с числом степеней свободы 6 и доверительной вероятностью 0,95. В знаменателе 2,45 — корень квадратный из 6.
Доверительный интервал для среднего квадратичного отклонения:
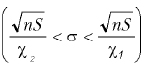
Если мы зададим уровень значимости 0,05, то χ1 — критическое значение распределения хи-квадрат с уровнем значимости 1–0,05/2 и числом степеней свободы (5–1) — будет равняться 0,831. χ2 — критическое значение распределения хи-квадрат с уровнем значимости 0,05/2 и числом степеней свободы (5–1) будет равняться 12,832. Тогда доверительный интервал примет вид (2,45* 8,008/12,832 ;2,45* 8,008/0,831) = (1,53; 23,61)
Как видите, доверительные интервалы достаточно велики. Это связано с тем, что присутствует большая дисперсия (рассеяние данных), и, чтобы обеспечить заданную вероятность (0,95) попадания среднего и среднеквадратичного отклонения в заданный интервал, необходимо увеличивать последний. Что мы и наблюдаем.
2.4.5. Определение параметров с использованием электронной таблицы Excel
Большинство из описанных параметров и характеристик (за исключением сгруппированных данных) могут быть вычислены с использованием электронной таблицы Excel. В таблице 2.12 приводятся не все функции, имеющие отношения к законам распределения, так как в каждом разделе книги приводятся только те функции, которые в нем используются. Дополнительную информацию можно найти в предметном указателе в конце книги.
Таблица 2.12
Описание некоторых функций
| Название параметра | Название функции англ./рус. | Описание параметров |
| Среднее | AVERAGE/СРЗНАЧ | Перечень значений или интервал имен ячеек |
| Медиана | MEDIAN/МЕДИАНА | Перечень значений или интервал имен ячеек |
| Мода | MODA/МОДА | Перечень значений или интервал имен ячеек |
| Дисперсия | VAR/ДИСП | Перечень значений или интервал имен ячеек |
| Среднее квадратичное отклонение | STDEV/СТАНДОТКЛОН | Перечень значений или интервал имен ячеек |
| Нормальное распределение (фактически рассчитываются значения функций j и F, которые обычно используются в виде таблиц) | NORMDIST/НОРМРАСП | (x; среднее; стандарт_откл; условие)
X — это значение, для которого строится распределение. Среднее — среднее арифметическое распределения. Стандарт_откл — стандартное отклонение распределения. Условие — логическое значение, определяющее форму функции. Если оно имеет значение ИСТИНА, то функция НОРМРАСП возвращает интегральную функцию распределения; если это аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения.
|
| Распределение Пуассона | POISSON/ПУАССОН | (x; среднее; условие)
X — количество событий. Среднее — ожидаемое численное значение. Условие — логическое значение, определяющее форму возвращаемого распределения вероятностей. Если аргумент имеет значение ИСТИНА, то функция ПУАССОН возвращает интегральное распределение Пуассона, то есть вероятность того, что число случайных событий будет от 0 до x включительно; если этот аргумент имеет значение ЛОЖЬ, то возвращается функция плотности распределения Пуассона, то есть вероятность того, что событий будет в точности x. |
| Среднее геометрическое | GEOMEAN/СРГЕОМ | Перечень значений или интервал имен ячеек |
| Полуширина доверительного интервала | CONFIDENCE/ДОВЕРИТ | (альфа, среднее квадратичное, число опытов)
альфа — уровень значимости, обычно 0,05 |
| Среднее гармоническое | HARMEAN/СРГАРМ | Перечень значений или интервал имен ячеек |
Рассмотрим пример использования основных функций. На рис. 2.27 приведена копия экрана с примером. В ячейках от C2 по H2 помещены исходные данные. В ячейках от G5 по G9 и H9 помещены функции, вычисляющие необходимые нам параметры (см. табл. 2.13).
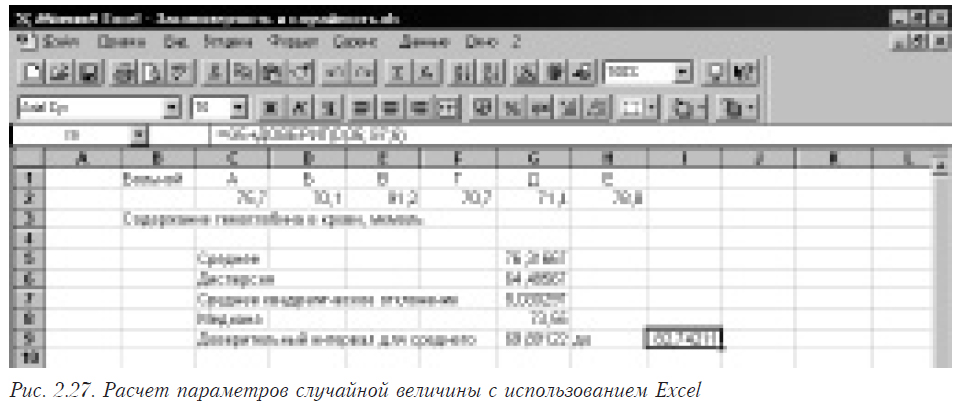
Таблица 2.13
| Имя ячейки | Содержимое |
| G5 | =СРЗНАЧ(C2:H2) |
| G6 | =ДИСП(C2:H2) |
| G7 | =СТАНДОТКЛОН(C2:H2) |
| G8 | =МЕДИАНА(C2:H2) |
| G9 | =G5-ДОВЕРИТ(0,05;G7;СЧЁТЗ(C2:H2)) |
| H9 | =G5+ДОВЕРИТ(0,05;G7;6) |
Вы видите, что H9 в функции ДОВЕРИТ(0,05;G7;6) явно указано число опытов (6), а в G9 в такой же функции ДОВЕРИТ(0,05;G7;СЧЁТЗ(C2:H2)) для определения числа опытов используется функция СЧЁТЗ(C2:H2), параметрами которой являются диапазон используемых ячеек, а результат — их число.
Допустим, мы имеем данные, по которым необходимо построить гистограмму (рис. 2.28).

Сначала необходимо задать интервалы, в которых будем считать частоты появления случайной величины. В данном случае мы выбрали одинаковые интервалы, длиной 4 единицы. Границы интервалов поместили в столбик G (рис. 2.29).

То есть мы имеем интервалы (0,24): (25,28) и т д. После этого в ячейке Н3 набираем формулу =ЧАСТОТА[FREQUENCY](B3:F17;G3:G12). Первый ее параметр описывает поля, в которых находятся исходные данные, а второй — поля, в которых записаны правые границы интервалов. После ввода формулы осталось лишь “растянуть” ячейку Н3 до Н12 в них будут размещаться частоты, соответствующие интервалам. Результат приведен на рис. 2.30.

Построить по столбцу частот графическое изображение гистограммы не составит труда.
Возможно построение гистограммы с помощью функции, имеющейся в “Анализе данных”. Для этого в меню последовательно выбирается “Сервис”, “Анализ данных”. В появившемся окне (см. рис. 2.31) выбирается “Гистограмма”.

После этого появляется окно, в котором необходимо задать исходные данные для построения гистограммы (см. рис. 2.32).
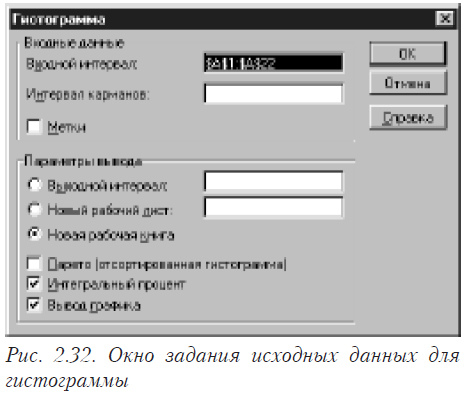
Параметры диалогового окна «Гистограмма» имеют следующее назначение.
Входной диапазон
В этом окне необходимо задать ссылку на диапазон ячеек, в которых находятся исходные данные. Исходные данные должны представлять собой перечень значений, а не частоты!.
Интервал карманов (необязательный)
Введите в поле диапазон ячеек и необязательный набор граничных значений, определяющих отрезки (карманы). Эти значения должны быть введены в возрастающем порядке. В Microsoft Excel вычисляется число попаданий данных между текущим началом отрезка и соседним большим по порядку, если такой есть. При этом включаются значения на нижней границе отрезка и не включаются значения на верхней границе.
Если диапазон карманов не был введен, то набор отрезков, равномерно распределенных между минимальным и максимальным значениями данных, будет создан автоматически.
Метки
Ставится отметка, если первая строка или первый столбец входного интервала содержит заголовки. Если заголовки отсутствуют; названия для данных выходного диапазона создаются автоматически.
Выходной диапазон
Вводится ссылку на левую верхнюю ячейку выходного диапазона. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные.
Новый лист
Устанавливается переключатель, чтобы открыть новый лист в книге и вставить результаты анализа, начиная с ячейки A1.
Новая книга
Чтобы открыть новую книгу и вставить результаты анализа в ячейку A1 на первом листе в этой книге устанавливается переключатель. Если вы хотите получить график это нужно обязательно сделать.
Парето (отсортированная диаграмма)
При выборе этой возможности, данные представляются в порядке убывания частоты. В математической статистике такая форма гистограммы не используется.
Интегральный процент
Рассчитываются значения и строится график накопленной частоты.
Вывод графика
Устанавливается флажок для автоматического создания встроенной диаграммы. Внимание! Если вы хотите построить график, то обязательно нужно задавать “Новая книга”.
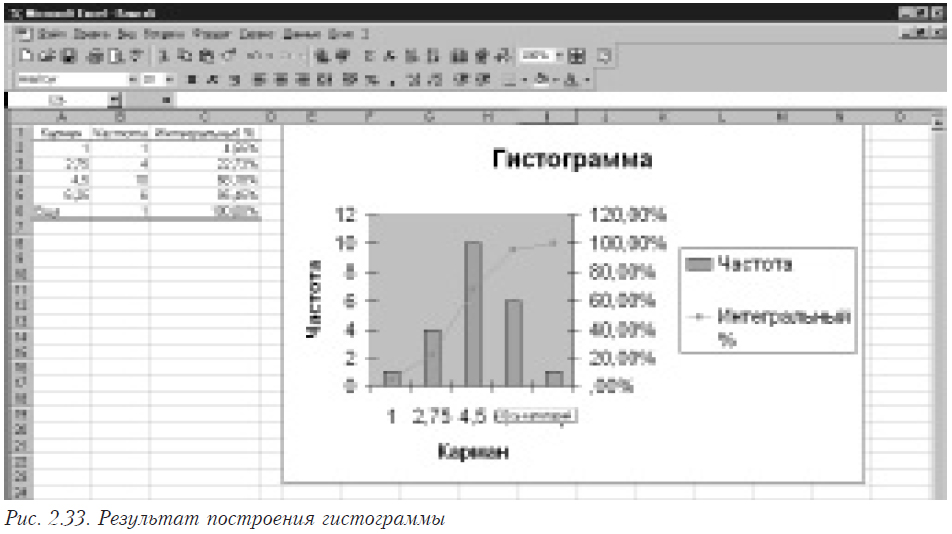
Результаты построения гистограммы приведены на рисунке 2.33.
Литература
- Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: исследование зависимостей. — М.: Финансы и статистика, . — 487 с.
- Браунли К.А. Статистическая теория и методология в науке и технике.— М.: Наука ГРФМЛ.— 407 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. –М.: Высшая школа, 1977. 479 с.
- Закс Л. Статистическое оценивание.— М.: Статистика, 1976.— 598 с.
- Кимбл Г. Как правильно пользоваться статистикой.— М.: Финансы и статистика, 1982.— 294 с.
- Уильям Кохрен Методы выборочного исследования. – М.: Статистика 1976. – 440 с.
- А.Н. Кудрин, Г.Т. Пономарева Применение математики в экспериментальной и клинической медицине. – М.: Медицина. 1967. – 356 с.
- С.Н. Лапач, А.В. Чубенко Применение современных количественных методов анализа в фармакологии и фармации // Фармакологічний вісник.— 1999.— № 1. — Додаток № 1. — 140 с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка. – К.: ЗАО “Укрспецмонтажпроект”, 1999. – 312 с.
- Н.А. Плохинский Алгоритмы биометрии. – М.: МГУ. – 1980. – 150 с.
- Поллард Дж. Справочник по вычислительным методам статистики.— М.: Финансы и статистика, 1982.— 344 с.
- Справочник по прикладной статистике. В 2-х т. Т. 1: Пер. с англ. / Под ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина.— М.: Финансы и статистика, 1989. — 510 с.: ил.
- Справочник по прикладной статистике В 2-х т. Т. 2: Пер. с англ. — М.: Финансы и статистика. – 1990.— 526 с.: ил.
- Секей Т. Парадоксы в теории вероятностей и математической статистике. — М.: Мир. – 1990.— 240 с.
- Спрент П. Как обращаться с цифрами, или статистика в действии / Пер. с англ. А.Ф. Якубова. — Мн.: Выcш. шк. – 1983. — 271 с.
- Дж. Теннант-Смит Бейсик для статистиков – М.: Мир. – 1973. — 208 с.
- П.В. Терентьев, Н.С. Ростова Практикум по биометрии. – Л.: ЛГУ. – 1977. – 152 с.
- Тюрин Ю.П. , Макаров А.А. Статистический анализ данных на компьютере. — М.: ИНФРА-М. – 1998. — 528 с.
- А. Бредфорд Хилл Основы медицинской статистики М.: — Медгиз. – 1958. – 306 с.
- Хургин Я.И. Как объять необъятное.— М.: Знание. – 1985.— 192 с.
- Эльясберг П.Е. Измерительная информация: сколько ее нужно? как ее обрабатывать? — М.: Наука. – 1983.— 208 с.