Статистика не должна состоять в одном только заполнении ведомостей размером в двуспальную простыню никому не нужными числами, а в сведении этих чисел на четвертушку бумаги и в их сопоставлении между собой, чтобы не только видеть, что было, но и предвидеть, что будет.
А.Н. Крылов
Регрессионный анализ является одним из наиболее широко используемых статистических методов. Этот же метод является причиной наибольшего числа разочарований и ошибочных выводов. Это связано с тем, что на самом деле регрессионный анализ — это довольно длинная технологическая цепочка обработки данных. С одной стороны, в ней задействовано большое количество других статистических процедур (гипотезы о средних и дисперсиях, корреляционный и дисперсионный анализ, планирование эксперимента и пр.), а с другой — разделы других наук (например, линейная алгебра). Такая сложность вызывает ряд взаимосвязанных проблем в его применении.
Поэтому сразу хотелось бы предупредить; решение сложных регрессионных задач с использованием средств Excel невозможно. Для больших и сложных задач необходимо использовать статистические пакеты. Лучше всего регрессионный анализ реализован в программных средствах ПРИАМ[1] и BMDP. Мы же предлагаем ряд программ и таблиц, которые позволят вам эффективно решать сравнительно небольшие задачи.
Назначение
Получение по экспериментальным данным математических моделей, описывающих поведение некоторой характеристики в зависимости от изменения множества факторов, то есть
![]()
где Y — зависимая переменная (отклик); X1,X2,…Xm — независимые переменные (факторы); e — случайная ошибка.
6.1. Общие сведения
Возьмем группу задач, в которых изучается объект или процесс, подвергающийся влиянию несколько факторов. Результаты функционирования процесса в общем случае также описываются несколькими параметрами.
Для рассматриваемой группы задач характерно представление изучаемого процесса, объекта или явления в виде «черного ящика» (см. рис. 6.1). Такое представление является одним из самых распространенных подходов к решению задач в кибернетике и анализе сложных систем.
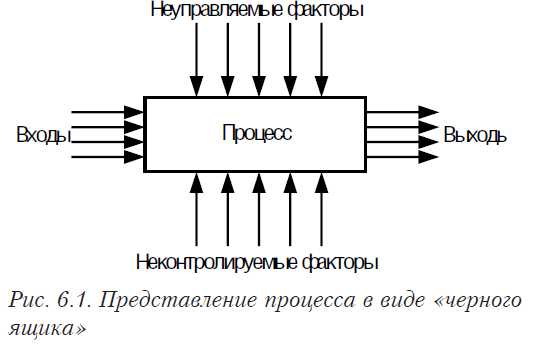
Здесь, под входами подразумеваются независимые переменные, которыми мы можем управлять. Выходы — это переменные, которые служат характеристикой изучаемого процесса. Неуправляемые факторы — независимые переменные, значения которых можно измерить, но управлять ими нельзя. Неконтролируемые факторы —влияют на процесс, но мы их не можем измерить (или даже не знаем какие они).
Основывается регрессионный анализ на методе наименьших квадратов (МНК), суть которого состоит в следующем.
Допустим, у нас есть матрица условий эксперимента Х (размерности nґm) и вектор результатов Y. Необходимо получить аппроксимирующую функцию Y = F(X). Для того, чтобы получить однозначное решение, вводится дополнительное условие — аппроксимация должна быть таковой, чтобы минимизировать следующий функционал:
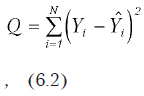
Здесь Yi — значение зависимой переменной в i-ом опыте (всего их N); — значение, рассчитанное по аппроксимирующей функции для i-ого набора переменных Х. То есть сумма квадратов отклонений предсказанных значений от экспериментальных должна быть минимальной.
Для линейного регрессионного анализа принята общая форма функции:
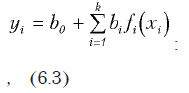
где fi(xi) — некоторая функция от исходных переменных.
Для того, чтобы найти неизвестные коэффициенты bi и удовлетворить условие (6.2), необходимо подставить вид функции из (6.3) в (6.2). Затем взять частные производные от Q по неизвестным bi, подставить известные значения хi и приравнять полученные выражения к нулю.
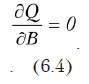
Из совокупности уравнений вида , подставив вместо Yi значение выражения (6.3), получим систему уравнений (в матричной форме записи)
![]()
где B — вектор неизвестных коэффициентов регрессии; Y — вектор результатов экспериментов (значения отклика); Х — условия эксперимента (значения независимых переменных); T — знак трансформированной матрицы. Как результат решения этой системы находим коэффициенты регрессии. При этом используется метод Гаусса с ведущим элементом.
К недостаткам МНК относится его неустойчивость к выбросам — при их наличии модель слишком «перетягивается» к выделяющимся наблюдениям и искажается. Вообще говоря, оценки по методу МНК совпадают с оценками по максимуму правдоподобия только для случая нормального распределения ошибок. Во всех остальных случаях необходимы корректировки оценок или использование других методов. Поэтому, когда предполагается возможность выбросов, используют метод наименьших модулей (МНМ), в котором минимизируется функционал
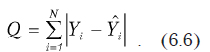
Если матрица эксперимента ортогональна, система распадается на отдельные уравнения, независимые друг от друга, а коэффициенты регрессии находят по формуле
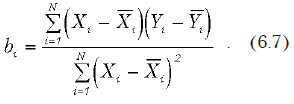
Предпосылки
В классическом регрессионном анализе для получения оценок коэффициентов модели y = b0 + Sbixi + e и возможности анализа их свойств необходимо выполнение ряда допущений и предпосылок. Допущения выводятся из теории Гаусса — Маркова, из которой следует, что:
- В каждом опыте математическое ожидание случайной ошибки ei равно нулю M[ei] = 0, i=1..N;
- Во всех опытах дисперсия постоянна и одинакова — D[ei] = s2 = const, i = 1..N.
- Ошибки в любых двух опытах независимы — cov[ei,ej] = 0, где i, j О [1,N], i ¹
В этом случае оценки коэффициентов регрессии, полученные по методу наименьших квадратов, будут несмещенными, состоятельными и наилучшими в классе линейных несмещенных оценок.
Для того, чтобы можно было проверить гипотезы об истинном значении параметров модели и построить интервальные оценки для коэффициентов, вводится еще одно допущение: ошибка ei в каждом опыте имеет нормальный закон распределения
ei~ N(.), i=1..N.
Все вышеизложенные допущения можно записать в общем виде
E ~ Nn(0,s2In).
Кроме представленных допущений вводятся следующие предпосылки:
- Матрица наблюдений имеет полный ранг (фактически подразумевается матрица, по которой находятся коэффициенты регрессии).
- Значения случайной ошибки ei не зависят от значений независимых переменных.
- Матрица наблюдений является детерминированной (или другими словами, ошибки регистрации независимых переменных пренебрежимо малы по сравнению со случайной ошибкой ei).
- Структура модели известна и задана.
Саттерзвайтом[2] выдвинуто предположение о том, что значимость эффектов, ответственных за протекание исследуемого процесса, убывает по экспоненциальному закону. В [15] доказано, что введение этого допущения необходимо для правильного определения структуры. Решение сотен практически задач показывает, что это допущение почти всегда выполняется.
Примечание:
- При невыполнении допущений и предпосылок возникают различные проблемы, которые ухудшают качество модели или даже делают ее непригодной к использованию.
- В нашей работе рассматривается только линейный регрессионный анализ (полное название — линейный по параметрам регрессионный анализ). Это означает, что функция представляет собой линейную комбинацию некоторых других функций, зависящих от независимых переменных. Эти функции могут быть достаточно сложными. Нелинейный регрессионный анализ следует использовать только в случае крайней необходимости. Причина в том, что его использование, во-первых, теоретически не обосновано [35], а во-вторых, при поиске коэффициентов почти всегда образуются плохо обусловленные матрицы, вследствие чего полученные модели будут неустойчивыми.
6.2. Формализация задачи
Математика, подобно жернову перемалывает лишь то, что под нее засыпают. Как, засыпав лебеду, вы не получите пшеничной муки, так, исписав целые страницы формулами, вы не получите истины из ложных предпосылок.
Томас Гексли
Все великолепие Вселенной четко выражается для них (животных — авт.) в виде а) того, с чем спариваются; б) того, что едят; в) того, от чего убегают, и г) камней. Это освобождает животных от ненужных мыслей и придает их сознанию остроту, направленную только на то, что действительно необходимо.
Терри Пратчет «Творцы заклинаний»
Ошибка, допущенная в первоначальной расстановке сил, едва ли может быть исправлена в ходе всей войны.
Мольтке
Формализация является первым этапом решения любой задачи. От того, насколько правильно выполнена формализация, зависит выбор средств, методов и эффективность решения. Ошибки, допущенные на этом этапе, очень трудно, а иногда невозможно исправить в процессе обработки результатов эксперимента. Поэтому мы рекомендуем как можно тщательнее выполнять фармализацию, привлекая для этого всю имеющуюся информацию. При формализации осуществляется перевод цели исследования в вид, пригодный для обработки методами статистического анализа. Следует помнить, что больше всего ошибок происходит на этом этапе. Особенно следует опасаться ситуации «выхолащивания» или изменения цели решаемой задачи, когда в результате неправильно выполненной формализации решается не та задача, или полученное решение не имеет никакого практического значения. Поэтому, после формализации, следует провести верификацию полученных результатов. Необходимо ответить на вопрос: позволяют ли эти результаты достичь поставленных целей исследования?
Формализация включает в себя следующие действия:
- Формулировку четких целей в терминах предметной области.
- Определение прикладной цели исследования.
- Анализ и структурирование объекта исследования.
- Выбор средств и методов решения.
- Определение необходимых ресурсов для проведения исследований.
Четких границ между перечисленными пунктами, как правило, не существует, так как они взаимосвязаны. Например, наличные ресурсы для проведения исследований определяют объем информации, которую можно получить. Таким образом, ресурсы косвенно определяют возможность достижения цели.
6.2.1. Определение прикладной цели исследования
От прикладной цели исследования зависит выбор методов, она же определяет потребность в ресурсах.
Прикладные цели исследования могут быть следующими:
- Аппроксимация некоторого множества данных моделью.
- Поиск оптимальных условий.
- Определение структуры связей между зависимыми и независимыми переменными и получение модели, отражающей эту структуру.
В общем случае под аппроксимацией понимается замена некоторой таблицы формулой. При этом значения, рассчитанные по формуле, должны с наперед заданной точностью соответствовать табличным данным. В таких задачах статистические характеристики модели практически не имеют никакого значения. Однако выбрав эту цель, необходимо помнить о возможных опасностях, которые подстерегают исследователя на этом пути.
Добиваясь высокой точности в узлах (точках эксперимента или клетках таблицы), без учета статистических характеристик, можно оказаться перед фактом, что в промежутках между точками эксперимента значения, рассчитанные по модели, будут сильно отличаться от действительных. Это связано с тем, что попытки достичь максимальной точности в точках плана эксперимента без учета статистических характеристик модели приводят к переусложнению последней эффектами высших порядков и к явлению «осцилляции». При этом регрессионная кривая между аппроксимируемыми точками может принимать достаточно сложную форму, и интерполяция по такой формуле не имеет практического смысла. Поэтому, если вы собираетесь использовать модель для интерполяции, мы рекомендуем все-таки обращать внимание на ее статистические характеристики и проверить ее предсказующие свойства на контрольных точках, лежащих между узлами.
- Аппроксимация обычно используется при наличии изученного процесса, поведение которого описано таблицами, графиками, номограммами, а эти данные следует использовать в некоторых автоматизированных системах, где удобнее употреблять формулы. При выборе точек из таблиц, графиков и номограмм следует руководствоваться общими принципами планирования эксперимента, что облегчается отсутствием ограничений на количество экспериментов (для графических источников информации) и наличии полной информации о форме зависимости.
- Поиск оптимальных условий — задача, в которой необходимо найти точку в многофакторном пространстве. Кроме того, в такой задаче выполняются некоторые экстремальные условия (например, максимум некоторого показателя качества). При поиске оптимальных условий нет необходимости в какой-либо модели, поэтому он требует меньших ресурсов.
- В данной работе под построением модели мы понимаем построение линейной по параметрам регрессионной модели. Эксперимент при этом может быть натурным, полунатурным, вычислительным или результатом экспертного опроса. Модель должна быть такова, чтобы ее действительно можно было использовать для исследования объекта: соответствовать объекту не только по точности предсказания результата, — ее структура должна отражать действительную структуру связей между независимыми переменными и откликом. Обращаем ваше внимание на два момента, которые пользователь и статистик понимают по-разному, что может послужить причиной крупных ошибок и недоразумений. Первое — адекватность модели, второе — ее структура.
Пользователь обычно оценивает адекватность модели (то есть соответствие модели объекту) по среднему и максимальному проценту отклонения предсказуемых значений от экспериментальных. Но это не является статистической проверкой адекватности. В статистике для этого обычно применяют критерий Фишера. Модель может быть адекватной по критерию Фишера, но не удовлетворять требованиям пользователя по среднему и максимальному проценту отклонения.
Пользователь подразумевает, что частная структура модели всегда отвечает структуре связей объекта и на этом основании делает выводы о самом объекте. Подавляющее же большинство статистиков придерживается мнения о том, что структура модели не должна иметь никакого отношения к действительной структуре, пользователь может удовлетвориться любой моделью с хорошими статистическими критериями. Естественно, что пользователя это вряд ли устроит. На самом деле, такие модели очень тяжело построить, поэтому большинство статистиков неохотно берется за такую задачу.
Мы рассмотрели, какими могут быть цели исследования в чистом виде. На практике зачастую необходимо достичь одновременно нескольких целей, наиболее часто — получить модель и провести поиск оптимальных условий. В этой ситуации вам необходимо будет выбрать для реализации один из вариантов. Первый: сначала следует найти оптимальные условия функционирования объекта, а затем построить модель, описывающую поведение объекта в оптимальной области. Второй: сначала необходимо построить математическую модель для описания всей области исследования, и затем по модели с помощью вычислительного эксперимента найти оптимум. Выбор подхода определяется наличием необходимых ресурсов и конкретизацией поставленной прикладной задачи. После определения цели вы переходите к следующему этапу формализации.
6.2.2. Анализ и структурирование объекта исследования
Никогда не строй планов, не выведав о противнике все, что можно. Не бойся менять планы, если получил новые сведения. Никогда не думай, что тебе известно все. И никогда не жди, пока узнаешь все.
Роберт Джордан, «Властелин Хаоса»
Выбор переменных и требования к ним
При анализе и структурировании объекта исследования выбираются зависимые переменные (отклики); составляется перечень независимых переменных и определяется состав контролируемых неуправляемых и управляемых переменных; уровни варьирования для управляемых и уровни фиксации для переменных, не включаемых в модель. Зависимые переменные представляют собой показатели, по значениям которых мы собираемся оценивать течение процесса.
Зависимые переменные (отклики) должны отвечать следующим требованиям:
- Иметь физический смысл и достаточно полно характеризовать исследуемый объект, процесс или явление.
- Быть воспроизводимыми, то есть при повторении опытов в номинально одинаковых условиях полученные значения должны совпадать с точностью до ошибки эксперимента.
- Каждому набору значений независимых переменных должно соответствовать одно (с точностью до случайной ошибки) значение отклика.
- Иметь измеряемые значения при любой комбинации выбранных уровней факторов.
Независимые переменные (факторы) должны отвечать следующим основным требованиям:
- Должны быть управляемыми (возможность устанавливать и поддерживать необходимые значения в процессе эксперимента).
- Не должны зависеть от других переменных (возможность независимо от остальных факторов управлять каждой переменной).
- Область совместного существования независимых переменных должна представляет собой гиперпараллелепипед, то есть в пределах заданных границ измерения переменных допустимы любые их сочетания. Никакие комбинации факторов не должны приводить к нежелательным последствиям (например, разрушение установки, качественное изменение процесса или явления, при котором изучаемый отклик не существует). В случае невыполнения этого условия см. 6.3.5.
- Должны быть детерминированными величинами.
- Интервал изменения каждой независимой переменной не должен быть слишком мал, так как при малом интервале изменения переменная может не оказывать значительного влияния на отклик. Нежелательно устанавливать интервал, равный требованиям технических условий или допуска — изменение переменной в таком интервале, как правило, не оказывает значительного влияния на отклик.
Вместе с тем, интервал не должен быть слишком широк, так как в очень большом интервале изучаемый объект или процесс могут вести себя достаточно сложно и для надежного описания может оказаться недостаточно выделенных ресурсов.
Уровни варьирования факторов должны выбираться с учетом: априорной информации о характере частного влияния на отклик каждой переменной; точности поддержания уровня значения фактора; разрешающей способности контрольно-измерительной аппаратуры; методов регистрации; вида зависимости отклика от данной переменной. Так, при линейной зависимости достаточно двух уровней, при параболической — трех и т.п. Если априорная информация о виде зависимости отсутствует, число уровней желательно брать с запасом (4–8).
Значения уровней желательно размещать равномерно по интервалу варьирования. В случае необходимости (в целях получения полезной информации) неравномерное размещение уровней, значений уровней внутри интервала исследователь устанавливает в нужных ему точках. Но при этом нельзя допускать, чтобы соседние значения уровней варьирования очень различались (в 8–10 и более раз). Это приведет к ухудшению статистических свойств матрицы независимых переменных. Рекомендуется в этом случае перейти к логарифмической шкале для данной переменной, в рабочей матрице xi заменить на logxi.
- Независимые переменные должны быть однозначны: одному значению независимой переменной отвечает одно (с точностью до случайной ошибки) значение отклика.
- Совокупность выбранных независимых переменных должна отвечать требованиям совместимости (все их комбинации осуществимы и безопасны). Более подробно см. 6.3.5.
- Выбор факторов должен быть полным. Это означает, что выбранной группы факторов должно быть достаточно для объяснения поведения зависимых переменных (откликов).
- Точность фиксации факторов должна быть высокой. Это означает, что минимальная разница между значениями соседних уровней варьирования переменных должна быть, по крайней мере, на порядок выше точности установки данного параметра.
По результатам анализа и структуризации объекта исследования заполняются таблицы, содержащие информацию о независимых управляемых, неуправляемых, но контролируемых и фиксируемых в процессе эксперимента, и зависимых переменных. Для управляемых независимых переменных в таблицу должна быть занесена следующая информация: название переменной и единицы измерения, значение уровней варьирования и точность поддержания этих уровней. Должны быть перечислены независимые переменные, не изменяемые в эксперименте, и их значения. Желательно также перечислить переменные, которыми нельзя управлять, но которые могут оказывать существенное влияние на отклик (например, погодные условия), и затем измерить их при проведении эксперимента. При ограничениях на комбинацию взаимных значений уровней варьирования следует описать разрешенные (запрещенные) комбинации или привести графическое изображение разрешенной области значений. Для всех зависимых значений следует привести названия, единицы измерений, если это косвенные измерения — методику измерения или ссылку на нее. Если в дальнейшем предстоит оптимизация по моделям, желательно определить цели оптимизации по каждой модели и соотношения этих целей между собой (равноправие или преимущество одних целей над другими).
Выбор средств, методов решения, а также необходимых ресурсов зависит от цели работы. Наиболее трудоемкой и сложной, требующей значительных ресурсов, является задача определения структуры связей между независимыми и зависимыми переменными.
При планировании эксперимента на этапе выбора уровней варьирования нужно внимательно следить за тем, чтобы не получить разрывную неоднородную область эксперимента, которая в случае, если при изменении независимой переменной от одного уровня к другому качественно изменяется реакция отклика. Например, один и тот же препарат может оказывать различное влияние на течение болезни у мужчин и женщин (вплоть до противоположного). В таких ситуациях при построении модели вы, в лучшем случае, получите информацию, которая не соответствует действительности. В худшем — вам не удастся построить информативную и адекватную модель.
В таком случае необходимо строить отдельную модель для каждой такой области: например, модель влияния препарата на организм мужчины и модель, описывающая его влияние на организм женщины (см. 6.5.3).
Хотим обратить особое внимание на нецелесообразность попыток переложить работу, которую должен сделать человек, на вычислительную машину. Наиболее распространенной ошибкой является то, что вместо анализа исходного состояния и выбора наиболее представительных 10–20 факторов, берут несколько десятков факторов, в надежде, что затем машиной будет выполнен отбор. Поэтому, пользователь должен помнить:
- При использовании практически всех программных средств, при большом количестве анализируемых регрессоров, результаты резко ухудшаются.
- Чем больше независимых переменных вы хотите включить в модель, тем больше требуется ресурсов для ее надежного получения. Дело в том, что для надежного определения зависимости необходимо анализировать не только линейные члены (исходные факторы), но и члены второго и, возможно, более высоких порядков, а также взаимодействия. Это связано с тем, что фактическая зависимость может быть сложнее, чем линейная.
- Физическая сложность качественного проведения эксперимента растет при этом быстрее, чем количество требуемых ресурсов.
- Следствием усложнения эксперимента является повышение уровня влияния случайных факторов, то есть — уровня «шума» (увеличение дисперсии воспроизводимости).
- В таких экспериментах получается, что вместо нескольких сильно влияющих факторов у нас есть много очень слабо влияющих, которые только в совокупности обеспечивают значимое влияние на отклик. В таком случае уменьшается надежность правильного определения структуры.
В связи с вышеизложенным мы не рекомендуем усложнять эксперимент — затратив большие ресурсы, вы не получите желаемого результата. Как поступать в случае, когда вы используете данные пассивного эксперимента, можно узнать из 6.4.3.
6.2.3. Определение требуемых ресурсов для проведения исследования
Позитивные принципы стратегии:
- Выбирайте цель по своим средствам.
- Никогда не забывайте о цели, когда вы приводите свой план в соответствие с изменившейся обстановкой.
Б.Х. Лидден Гарт
«Стратегия непрямых действий»
Количество необходимых ресурсов в значительной степени зависит от числа опытов. Здесь предполагается, что все опыты стоят одинаково, поэтому количество требуемых ресурсов прямо пропорциональны числу опытов.
Если целью исследования является одновременно получение математической модели и поиск оптимальных условий, то обычно сначала строится модель, а затем по модели производится поиск оптимальных условий. Часто выделенных ресурсов недостаточно для гарантированного получения хорошей математической модели. В такой ситуации рекомендуется инвертировать задачу, то есть сначала найти оптимальные условия (на что требуется меньше ресурсов), а затем построить модель для части факторов, зафиксировав остальные в области оптимума, которая значительно меньше всей исследуемой области. При таком подходе в задачах со значительным числом исследуемых факторов, удается получить результат при меньших затратах на эксперимент.
Если целью исследования является определение структуры связей или аппроксимация, необходимое число опытов (без учета дублирования) определяется по формуле
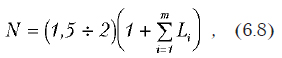
где m — число независимых переменных; Li — максимальная предполагаемая степень аппроксимационного полинома по i-му фактору. Это формула базируется на предположении Саттерзвайта о том, что относительное распределение силы влияния эффектов, ответственных за процесс происходит по экспоненциальному закону [15]. Она будет верна также и для случая линейного убывания силы влияния. По нашим наблюдениям, примерно в 95% задач данное предположение соответствует реальности.
Обычно Li = Fi – 1, где Fi — число уровней варьирования каждой независимой переменной. При большом числе уровней (6 и более) обычно достаточно 4-ой степени. При поиске оптимальных условий число экспериментов определяется формулой
![]()
где р — вероятность попадания в область оптимума; q — доля пространства, содержащая область оптимума по отношению к ее общим размерам[3].
Например, при р = 0,99 и q = 0,1; N = 44. Значения p и q выбираются из априорных сведений о процессе, объекте. Для N рекомендуется брать значение, ближайшее к числу 2k (k — произвольное целое число) в связи с особенностями алгоритма генерации плана ЛПt-чисел.
Недостатком этой формулы с точки зрения практического применения является невозможность достоверной оценки для q. Эмпирически установлено, что значение q убывает с ростом размерности пространства (число независимых переменных). Для решения практических задач можно воспользоваться табл. 6.1.
Таблица 6.1
Количество опытов при поиске оптимальных условий
| Число независимых переменных | Число экспериментов |
| до 4 | 8 |
| 5–8 | 16 |
| 9–16 | 32 |
| 17–24 | 64 |
| 25–33 | 128 |
Максимально необходимое количество опытов для проведения экспериментальных исследований определяется по формуле:
![]()
где Nрасч — необходимое число опытов, определенное по формуле (6.8); Nконтр — число контрольных опытов; k1, k2 — кратность повторения экспериментов в обучающей и контрольной последовательности опытов соответственно; р — ожидаемая доля бракованных экспериментов, которые придется переделать.
Обычно, k1 = 2:3, k2 = 1, Nконтр = 0,25ґNрасч; р = 0,1. Разумеется, можно принять Nmax = Nрасч, но при этом необходимо учитывать возможные негативные последствия такого шага. Так, отсутствие контрольной выборки не позволяет надежно проверить предсказующие свойства модели. Отсутствие повторных экспериментов (при k1 = 1) не позволяет, во-первых, провести отбраковку аномальных наблюдений, а во-вторых, определить дисперсию воспроизводимости. При этом увеличивается вероятность неправильного определения структуры уравнения модели.
В такой ситуации, если задаваемая априорно дисперсия слишком велика, мы можем «недобрать» членов в модель, если слишком мала — «перебрать». В случае «недобора» мы не включим в модель эффекты, которые оказывают статистически значимое влияние на отклик, а при «переборе» в модель попадут «шумовые» эффекты. И то и другое нежелательно.
Количество откликов (зависимых переменных) не влияет на количество требуемых ресурсов за исключением следующих ситуаций:
- измерение одной из зависимых переменных на изучаемом объекте приводит к неконтролируемому искажению значения другой переменной;
- измерение значения переменной приводит к уничтожению объекта или изменению его состояния.
В таких случаях полученное необходимое значение опытов следует умножить на число зависимых переменных, которые не могут быть измерены на одном объекте.
При выполнении работ достигается компромисс между целями и выделенными ресурсами. Результатом работы является окончательный выбор уровней варьирования независимых переменных и выдача задания на генерацию плана в виде выражения
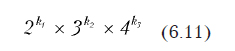
где k1, k2, k3 — число переменных, варьируемых соответственно на уровнях 2, 3… и т.д., N — число опытов плана эксперимента.
Для факторов, выбранных на этапе формализации задачи, составляется таблица соответствия натуральных и кодированных значений уровней варьирования, которая затем используется для построения рабочей матрицы эксперимента из матрицы планирования.
6.3. Конструирование плана эксперимента
Так как плохо спланированный опыт мало информативен, что нельзя исправить самой лучшей статистической техникой, то планирование эксперимента становится особо важным составным элементом статистики.
Л. Закс «Статистическое оценивание»
К сожалению, далеко не всеми экспериментаторами осознана необходимость специальной организации экспериментальных данных. Большинство под планированием эксперимента понимает календарное планирование или любую, неслучайным образом полученную, матрицу данных.
В связи с этим, мы считаем нужным рассказать о необходимости планирования эксперимента, то есть об организации матрицы независимых переменных специальным образом в соответствии с требованиями теории планирования эксперимента.
Вспомним о том, что регрессионный анализ с одной стороны опирается на статистические методы, с другой — реализован с использованием некоторых вычислительных процедур.
Корректное использование любых статистических выводов возможно лишь при удовлетворении имеющихся предпосылок и допущений. При их невыполнении мы не можем быть уверены в правильных выводах.
Одним из допущений регрессионного анализа является статистическая независимость объясняющих (независимых) переменных. Используемые при проверках различных гипотез критерии также требуют независимости переменных.
В основе процедуры получения оценок коэффициентов регрессии лежит решение системы линейных нормальных уравнений (см. (6.5). Вычислительные методы, реализующие эту процедуру, очень чувствительны к качеству матрицы, которое характеризуется числом обусловленности.
Указанные причины при плохих свойствах матрицы независимых переменных могут привести к:
- Неправильному определению структуры уравнения регрессии. В этом случае в модель будут включены не те эффекты, которые в действительности влияют на отклик. Такая модель может хорошо аппроксимировать обучающую выборку, но предсказующие ее свойства неудовлетворительны, не говоря уже об описании структуры связей.
- Получению неустойчивых оценок коэффициентов регрессии. В этом незначительные изменения результатов приводят к значительному (вплоть до перемены знака) изменению оценки коэффициента. Пользоваться такой моделью, разумеется, бессмысленно.
- Невозможности правильно пользоваться статистическими выводами, требующими независимости.
Пример влияния мультиколлинеарности на вычислительную устойчивость решения системы линейных уравнений[4]
На простом примере иллюстрируется влияние наличия мультиколлинеарности и ошибок во входных данных на результаты решения систем линейных уравнений (оценки коэффициентов регрессии получаются в результате решения системы нормальных уравнений XTXB = XTY).
В качестве примера взяты две системы из двух уравнений, имеющих одинаковые корни (табл. 6.2). Одна система — ортогональная, вторая — сильно закоррелированная. Приводятся результаты решения систем для случая когда ошибки отсутствуют и для случая, когда во сходных данных присутствует ошибка примерно в 6%.
Таблица 6.2
Системы уравнений и их корни
| Наличие ошибки | Ортогональная | Х1 | Х2 | Неортогональная | Х1 | Х2 |
| Нет | 2x1 + 5x2 = 17
-5x1 + 2x2 =1 |
1 | 3 | 2x1 + 5x2 = 17
6x1 + 14x2 = 48 |
1 | 3 |
| Есть | 2x1 + 5x2 = 17 + 1
-5x1 + 2x2 =1 |
1.06 | 3.17 | 2x1 + 5x2 = 17 + 1
6x1 + 14x2 = 48 |
-6 | 6 |
Из таблицы видно, что при решении ортогональной системы уравнений относительная величина ошибки в полученных корнях соответствует ее уровню во входных данных. В неортогональной системе ошибка резко увеличивается, искажая корни до такой степени, что изменяется даже их знак. Для ортогональной системы число обусловленности равно единице, а для неортогональной — достигает нескольких десятков, что и приводит к росту ошибки в результатах в тех случаях, когда есть ошибка во входных данных. При решении практических задачах (особенно экономических и социальных, в которых отсутствуют повторные опыты) наличие такой ошибки обычное явления. Вследствие этого, во-первых, неизвестна ошибка воспроизводимости. А во-вторых, каждый результат представляет собой случайную величину (а не оценку среднего, как в случае повторных опытов), естественно включающую в себя ошибку, величина которой неизвестна.
На рис. 6.2 и 6.3 приведена геометрическая интерпретация такой ситуации.
| 5 | ||||||||||
| 3 | ||||||||||
| 2 | ||||||||||
| 1 | ||||||||||
| -1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
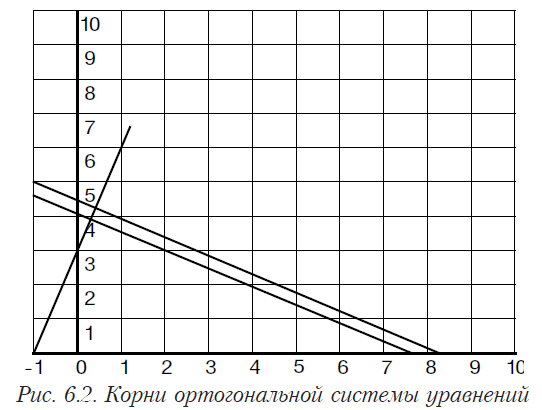
Мы видим, что присутствие ошибки приводит к паралельному переносу «истинной» прямой на небольшое растояние, соответствующее размеру внесенной ошибки. Вследствие этого переноса происходит и смещение точки пересечения прямых, которая является корнями системы уравнений. Для ортогональной системы, вследствии того, что угол пересечения равен 90, координаты точки пересечения смещаются пропорционально величине внесенной ошибки. Для неортогонального случая точка пересечения смещается очень сильно. Это смещение тем больше, чем меньше острый угол пересечения отрезков прямых, то есть, чем сильнее они закоррелированны.

В результате, мы не можем полагаться на статистические показатели качества модели и уверенно судить об области ее применения.
Чтобы избежать этих неприятностей, необходимо организовать матрицу независимых переменных таким образом чтобы последние были ортогональные или слабозакоррелированные.
Вопросами конструирования эксперимента занимается теория планирования эксперимента. Существует множество различных планов, каталоги и программы генерации, позволяющие получить оптимальные по заданному критерию планы.
С практической точки зрения основным недостатком существующей методологии является необходимость еще до эксперимента задать точную структуру уравнения регрессии (то есть перечисление эффектов, которые должны войти в модель). К сожалению, выполнить это требование практически никогда нельзя. В связи с этим, возникает задача конструирования робастных планов эксперимента, которые для любой (неизвестной заранее) структуры уравнения регрессии будут обеспечивать получение устойчивой, информативной и адекватной математической модели. Теоретически этот вопрос не решен.
Сначала нужно установить, какие статистические показатели матрицы плана определяют возможность построения модели, удовлетворяющей пользователя. Для этого определим требования, пригодные для практического использования в конструкторских и технологических разработках. На основании более чем 20-летнего опыта работы и решения сотен реальных задач мы можем утверждать, что с точки зрения пользователя пригодность модели определяется следующими условиями:
- Точность описания моделью процесса или явления должна быть достаточной для решения поставленной задачи.
- Структура модели должна отражать действительную структуру связей между факторами (независимыми переменными) и откликом.
Теперь постараемся привести эти пользовательские требования к конкретным статистическим критериями или условиям из регрессионного анализа.
Что касается первого условия, то его выполнение может быть получено за счет построения по критерию Фишера адекватной регрессионной модели. В этом случае, поскольку дисперсии статистически неразличимы, то и с точки зрения пользователя различить экспериментальные результаты и значение, предсказываемое моделью, не представляется возможным. Таким образом, условие выполнено.
Что касается второго условия, то вряд ли большинству читателей известно, что в прикладной статистике построение регрессионной модели со структурой, соответствующей реальной структуре взаимосвязи, считается чрезвычайно сложной задачей. Более того, многие статистики считают, что даже постановка такой задачи не имеет смысла, а пригодной следует считать любую модель, удовлетворяющую критерию адекватности со значимыми коэффициентами регрессии. К сожалению, при решении практической задачи таких моделей, равнозначных со статистической точки зрения, но разных по структуре, может быть несколько (даже несколько десятков).
Можно утверждать, что правильность и качество построенной модели находятся в существенной зависимости от степени закоррелированности регрессоров, включенных в модель.
Это связано, во-первых, с тем, что при закоррелированности регрессоров статистические критерии, используемые при построении и анализе регрессионной модели, также оказываются закоррелированными, что является нарушением предпосылок как регрессионного анализа, так и условий применения F- и t-критериев. В результате мы получаем прекрасную (если судить по основным статистическим показателям) модель, которая, однако, не имеет никакого практического смысла.
Во-вторых, поскольку коэффициенты регрессионной модели являются результатом решения системы линейных уравнений численными методами, то от свойств матрицы XТX (а в конечном итоге от свойств исходной матрицы X) очень зависят знак и значение регрессионных коэффициентов. Процесс решения численными методами системы линейных уравнений требует, чтобы матрица A в уравнении Ax = B была хорошо обусловлена, то есть число обусловленности (cond A) должно приближаться к единице. В противном случае мы имеем дело с неустойчивой системой, в которой даже знак коэффициентов регрессии (не говоря уже о величине) может не соответствовать истинному.
Требование хорошей обусловленности матрицы А = XТX автоматически ведет к требованию ортонормированности матрицы X.
6.3.1. Робастные планы эксперимента
Дело решается более строем, нежели числом
Маврикий «Тактика и стратегия»
Статистические и вычислительные условия требуют от нас ортогональности исходной матрицы. Причем полной ортогональности, как всех главных эффектов, так и всех анализируемых взаимодействий. Это возможно только в случае полного факторного эксперимента (ПФЭ), то есть полного перебора всех вариантов сочетаний значений уровней факторов. На практике это условие невыполнимо — число вариантов может изменяться от нескольких сот (в лучшем случае) до нескольких миллионов. Реализация такого количества экспериментов не представляется возможным. Поэтому следует пытаться построить план, в котором любая пара эффектов была бы как можно меньше закоррелированна. Величину этого «как можно меньше» установить довольно сложно, но на основании анализа данных, приведенных в специальной литературе, вычислительного эксперимента и обобщения опыта решения сотен практических задач мы сформулировали следующие требования к робастному плану эксперимента:
- число опытов в плане должно быть достаточным для описания модели наибольшей предполагаемой сложности;
- коэффициент парной корреляции между любой парой регрессоров, включая взаимодействия, не должен превышать 0,4;
- среднее значение коэффициента парной корреляции, рассчитанное по всем регрессорам, не должно превышать 0,08.
Для определения необходимого числа экспериментов мы рекомендуем пользоваться простой формулой (см. (6.8).
Проведенные нами вычислительные эксперименты показали, что если план отвечает сформулированным выше требованиям, то это служит гарантией построения информативной, адекватной и устойчивой модели (если таковую вообще можно построить на основании имеющихся данных).
Существует несколько способов конструирования робастных планов эксперимента.
Первый способ базируется на многофакторных регулярных планах. Это означает, что при выборе в каталоге (см. приложение З) или при генерации плана специальной программой (DESFACT) необходимо выбирать план с числом опытов в 1,5 — 2 раза превышающим суммарное число главных эффектов (см. (6.8).
Достоинства построенных таким образом планов:
- все главные эффекты и, обычно, часть взаимодействий взаимно ортогональны;
- очень часто матрица, по которой построена модель, является D-оптимальной.
К сожалению, эти планы имеют и ряд недостатков:
- как правило, часть регрессоров закоррелированна друг с другом с коэффициентами парной корреляции от 0,8 и выше;
- план не всегда полностью удовлетворяет всем требованиям робастности;
- план в общем случае не может быть достроен, то есть не может использоваться путь постепенного наращивания затрат с повышением сложности модели;
- выпадение хотя бы одного эксперимента приводит к существенному ухудшению статистических свойств матрицы планирования.
Принимая во внимание недостатки, был разработан второй способ конструирования робастных планов, базирующийся на последовательности ЛПt-чисел. В табл. 6.3 сравниваются основные характеристики двух типовых планов (план на базе МФРП и план на базе ЛПt-чисел).
Очевидно, что в целом статистические характеристики планов примерно равнозначны. Вместе с тем, планы на основе ЛПt-чисел имеют ряд преимуществ:
- одновременно являются и планами поиска оптимальных условий и позволяют более глубоко анализировать исследуемую область;
- могут быть использованы как последовательные, то есть затраты могут быть наращиваемыми постепенно и предыдущие результаты объединяются с последующими;
- при «выпадении» одного из экспериментов свойства плана ухудшаются в пределах, позволяющих его использовать.
Наиболее существенным недостатком таких планов считается необходимость выполнения экспериментов с числом уровней варьирования, равным числу опытов. Уменьшение числа уровней варьирования приводит к ухудшению статистических свойств. Кроме того, наилучшими свойствами обладают планы с числом опытов N = 2k, где k — любое целое число. Отступление от этого условия также ведет к незначительному ухудшению статистических свойств. Но ухудшение статистических свойств плана при числе опытов не равном 2k несущественно и практически не может повлиять на его качество (см. рис. 6.4).
Таблица 6.3
Сравнение статистических показателей планов
| Показатели | План на базе МФРП (35//27) | План на базе ЛПt -чисел (N=32, M=5) |
| 0<rij<10e-4 | 89,5 % | 51,5 % |
| 10e-4<rij<0,1 | — | 18,5 % |
| 0,1<rij<0,2 | — | 18,7 % |
| 0,2<rij<0,3 | 3,4 % | 6,5 % |
| 0,3<rij<0,4 | 8,2 % | 1,4 % |
| 0,4<rij<0,5 | 2,0 % | 0,4 % |
| 0,5<rij0<0,6 | 1,5 % | 0,2 % |
| 0,6<rij<0,7 | 0,7 % | — |
| 0,7<rij<0,8 | 0,7 % | — |
| 0,8<rij<0,9 | — | — |
| 0,9<rij<1 | — | — |
| rijср | 0,042 | 0,071 |
| cond* | 1 | 3,054 |
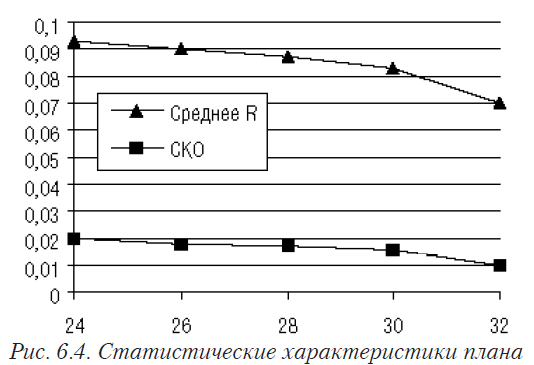
В случае, когда число уровней не равно числу опытов, сначала происходит очень незначительное ухудшение свойств плана, а затем — улучшение, что связано с фактическим превращением плана в план полного факторного эксперимента (см. рис. 6.5).
Данные для построение таких планов приведены в приложении И.
Существуют также планы «обобщенной свастики», предложенные А.Н. Ворониным, в которых число уровней также равно числу опытов.
Если многофакторные регулярные планы представляют собой регулярную пространственную решетку (рис. 6.6), то планы «обобщенной свастики» и планы на базе ЛПt-чисел имеют более сложную форму (см. рис. 6.7 и 6.8 соответственно).

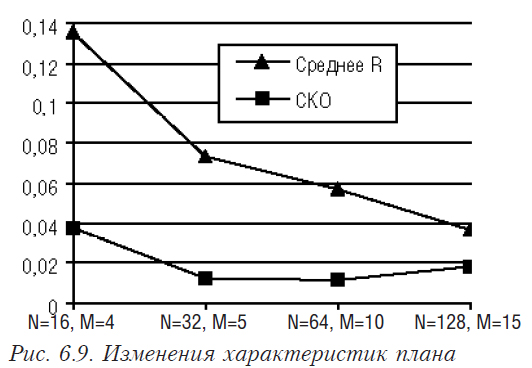
Из табл. 6.4 и рис. 6.9 видно, что с увеличением числа опытов характеристики планов в целом улучшаются. При этом изменяется (в лучшую сторону) и распределение коэффициентов корреляции по величине (см. табл. 6.4), резко уменьшается число больших значений коэффициентов корреляции (0,7 — 1,0), и общее рассеивание приводит к уменьшению разброса.
Из проведенного анализа следует, что при малом числе факторов (до 3 — 5) предпочтительно применять многофакторные регулярные планы, при увеличении числа факторов и в сложных ситуациях — ЛПt-планы как более надежные и позволяющие получить более подробную информацию о множественном уравнении регрессии.
Планы «обобщенной свастики» особенно эффективны при малом числе факторов (2 — 3) и очень малом числе опытов (5 — 6). В этой зоне они даже предпочтительнее, чем планы полного факторного эксперимента, поскольку при равном числе опытов имеют большее число уровней, что обеспечивает большие возможности по увеличению сложности модели. Кроме того, они обладают лучшими свойствами по «прощупыванию пространства» (то есть поиска оптимальных условий).
Таблица 6.4
Распределение коэффициентов корреляции для планов на базе ЛПt-чисел с 10 факторами и разным числом опытов
| Интервал | N = 16 | N = 32 | N = 64 | N = 128 |
| 0 | 40,3 | 50,4 | 48,5 | 91,3 |
| 0 — 0,1 | 11,7 | 18,9 | 33 | 7,5 |
| 0,1 — 0,2 | 10,2 | 15,8 | 13,8 | 0,8 |
| 0,2 — 0,3 | 8,1 | 7,8 | 2,7 | 0,2 |
| 0,3 — 0,4 | 5,4 | 3,3 | 0,6 | 0 |
| 0,4 — 0,5 | 3,7 | 1,6 | 0,5 | 0 |
| 0,5 — 0,6 | 2,0 | 0,5 | 0,5 | 0 |
| 0,6 — 0,7 | 1,2 | 0,2 | 0,1 | 0 |
| 0,7 — 0,8 | 0,8 | 0,2 | 0 | 0 |
| 0,8 — 0,9 | 1,7 | 0,4 | 0 | 0 |
| 0,9 — 1,0 | 15,1 | 0,7 | 0,3 | 0,2 |
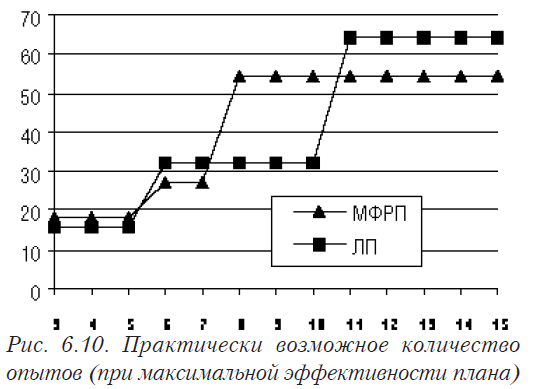
Что касается количества требуемых опытов, то для разных способов оно отличается незначительно, исключая зону в 8 — 10 факторов (см. рис. 6.10).
Конструировать план эксперимента можно либо с помощью средств ПС ПРИАМ[5], либо ПС DESFACT, либо вручную с использованием специальных таблиц (см. приложения И, З).
Полученный план представляет собой матрицу, каждая строка которой содержит кодированные значения независимых переменных для каждого уровня.
Квазиробастность в обоих случаях достигается выбором достаточного числа уровней для каждого фактора и числа опытов для всего плана, а также выбором многофакторного плана, отвечающего этим параметрам.
Таким образом, с точки зрения пользователя, робастность достигается правильным выбором числа уровней варьирования, так как число опытов после этого рассчитывается по формуле (6.8).Для того, чтобы выбрать число уровней варьирования, необходимо максимально задействовать имеющуюся информацию о процессе. Если известно, что при отдельном изменении некоторого Xi (остальные переменные зафиксированы) отклик изменяется по линейному закону, то для Xi достаточно два уровня, если по квадратичному — три и т.д. Если же такой информации нет, число уровней выбирается с запасом и с учетом ширины интервала изменения. При выборе значений уровней следует иметь в виду, что разница между ближайшими уровнями должна на порядок превышать возможную ошибку установки данной переменной.
Обычно 3 — 5 уровней вполне достаточно. Это связано с тем, что эксперименты проводят, как правило, в диапазоне изменений независимых переменных, представляющем незначительную долю области его существования.
Обычно значения уровней варьирования располагаются равномерно в интервале изменения независимой переменной. Но, если есть информация о неравномерном характере изменения функции (или какие-то точки представляют особый интерес), можно размещать значения уровней по интервалу так, как это необходимо.
На основании плана эксперимента в кодированных значениях составляется рабочая матрица наблюдений, каждая строка которой содержит условия проведения 1-го опыта и графы для занесения зависимых переменных (см. откликов).
Для многофакторных регулярных планов кодированные уровни представляют собой натуральные числа от 0 до числа, на единицу меньшего числа уровней (см. приложение В).
Для планов на базе ЛПt кодированные значения уровней представляют собой десятичные дроби в интервале от 0 до 1 (см. приложение И). Для этих планов переход от кодированных значений уровней к натуральным осуществляется по формуле
![]()
где
Xij — натуральное значение j-го фактора в i-ом опыте;
Qij — кодированное значение j-го фактора для i-ом опыта;
Xmax,j — максимальное значение j-го фактора;
Xmin,j — минимальное значение j-го фактора.
При конструировании плана эксперимента возможны ситуации, которые требуют некоторых нестандартных действий:
- Конструирование планов при включении неуправляемых контролируемых факторов.
- Конструирование плана при наличии неоднородностей.
- Конструирование плана при поиске оптимальных условий.
- Конструирование планов при нестандартной области планирования.
- Использование переменных, измеряемых в шкале наименований.
- Эксперименты, в которых присутствует «состав».
6.3.2. Конструирование плана эксперимента при включении неуправляемых контролируемых факторов
В нашем плане оказался лишь один изъян: мунтжак[6] не хотел запутываться в сети.
Дж. Даррел, «Только звери»
Одной из весьма распространенных задач является планирование экспериментов с необходимым включением в модель неуправляемых контролируемых факторов, оказывающих существенное влияние на изучаемый объект, процесс, явление (например, при учете погодных условий, фаз Луны и пр.). В таких ситуациях обычно рекомендуется проводить активно-пассивный эксперимент. Это не лучший выход из положения, так как подобный подход сводит на нет все преимущества планирования.
Для получения лучших результатов рекомендуется включать в план неуправляемые, но контролируемые переменные. Если фактор имеет несколько диапазонов изменения, то каждому диапазону ставится в соответствие один уровень. Значения уровней при этом будут иметь скорее всего качественный характер. При этом снижается точность моделирования, но появляется возможность использовать преимущества построения модели по данным активного эксперимента, и повышается вероятность правильного определения структуры уравнения регрессии.
При выполнении эксперимента приходится ждать, пока неуправляемые факторы примут соответствующее значение. Это резко увеличивает сроки проведения экспериментальных исследований, но улучшает качества получаемых моделей.
6.3.3. Конструирование плана эксперимента при наличии неоднородностей
При проведении многофакторного экспериментального исследования в неоднородных условиях возникает задача исключения или существенного уменьшения влияния источников неоднородностей на результаты, полученные в виде математической модели.
Обычно источниками неоднородностей являются, например, номинально одинаковые партии используемого сырья, лабораторные животные, стенды, технологическое оборудование, операторы и пр. Они образуют группу факторов, не входящих в матрицу планирования. Одним из возможных методов, применяемых в таких ситуациях, является разбиение плана эксперимента на ортогональные блоки.
Формально задача сводится к введению в план эксперимента дополнительного фактора (нескольких факторов, которые называются блоками) таким образом, чтобы все главные эффекты были ортогональными ко всем главным эффектам остальных факторов плана.
Под блоками понимается множество опытов плана, которым соответствует один и тот же уровень блокового фактора, если их несколько — одно и то же сочетание уровней блоковых факторов.
Необходимо стремиться к тому, чтобы возможные условия опытов внутри блока, которые не являются факторами в матрице планирования, были как можно более близкими для различных опытов.
Разбиение плана на блоки может быть произведено ПС DESFACT при задании параметра LBLMAX. При выборе плана из каталога необходимо включить в него дополнительный фактор, число уровней которого равно числу блоков, на которые мы разбиваем план.
С каждым уровнем блокового фактора связывается один и тот же уровень любого источника неоднородностей: одна партия сырья, один стенд, один объект технологического оборудования, один исполнитель и т.п. Если это не представляется возможным, необходимо ввести второй (третий и т.д.) блочный фактор и оставшиеся источники неоднородностей объединить в эти блоковые факторы. При этом различные блоковые факторы будут ортогональны друг другу, если не будут взаимодействовать между собой.
Такой подход позволяет вычленить влияние, как изучаемых факторов, так и источников неоднородностей и определить их вклад в результаты, что очень важно для принятия решений. Например, это дает возможность оценить, стоит ли тратить средства на устранение источников неоднородностей и на какие из них направить усилия в первую очередь.
6.3.4. Конструирование плана при поиске оптимальных условий
Для поиска оптимальных условий используются планы на основе ЛПt-чисел (до 51 фактора) или чисел Холтона (при большем числе факторов). Эти планы позволяют достаточно подробно прозондировать исследуемое пространство. При проведении экспериментов по поиску оптимальных условий рекомендуется следующая тактика. Вначале необходимо выполнить только часть экспериментов, например, — 16 первых из 32 запланированных. После их анализа принимается решение о дальнейших действиях, например:
- Прекратить дальнейшие эксперименты, так как требуемый уровень качества достигнут.
- Выполнить оставшиеся эксперименты, где точки распределены по всей области исследования.
- Сгенерировать новую матрицу и провести дополнительные опыты не по всей области, а в некоторой подобласти, которая локализована по результатам первой серии экспериментов.
Обратите внимание: проводить все запланированные эксперименты необязательно. Можно остановиться в любой точке, как только будет достигнут удовлетворяющий вас результат.
Рекомендуем после выбора оптимальной точки провести в ее окрестности несколько проверочных экспериментов, так как при отсутствии повторных опытов полученный результат мог быть случайным.
6.3.5. Конструирование плана эксперимента при нестандартной области факторного пространства
Нестандартная область планирования (не гиперпараллелепипед) довольно часто возникает в экспериментальных исследованиях вследствие ограничений на взаимные сочетания независимых факторов. Например, сочетания верхних значений температуры и давления приводит к разрушению установки, а при сочетании нижних уровней исследуемый процесс вообще не протекает.
Существуют следующие способы выхода из этой ситуации:
- Уменьшение области планирования с целью приведения ее к стандартному виду.
- Разбиение нестандартной области на несколько стандартных.
- Использование стандартной области. При этом эксперименты в «запрещенных» подобластях не проводятся, а значения отклика устанавливаются фиктивными.
- Генерация специального плана для области с ограничениями (например, с помощью ПС DESOPT).
- Преобразование нестандартной области планирования в стандартную путем замены ряда переменных на фиктивные.
Рассмотрим достоинства и недостатки перечисленных способов.
Первый способ является самым простым и легко реализуемым, но его использование не всегда возможно ввиду сложности области. Кроме того, применение этого способа очень часто приводит к выхолащиванию самой задачи.
Использование второго способа тоже не всегда возможно ввиду сложности области. Помимо этого, затраты возрастают пропорционально числу областей разбиения, возникает проблема анализа и совместного использования множества моделей.
Третий способ является самым опасным с точки зрения качества получаемой модели и выводов. Это связано с большим произволом в присвоении значений откликов в «запрещенных» областях, в результате чего может быть сильно искажена структура модели.
Четвертый способ теоретически является наиболее предпочтительным. Однако следует помнить, что существующие программные средства позволяют получить такой план далеко не всегда. Кроме того, полученный подобным образом план почти никогда не бывает робастным, более того, часто он бывает плохо обусловлен. Поэтому его применение на практике до разработки более совершенных планов невозможно.
Пятый способ можно применять при любом виде области. Его преимущество в том, что планирование и обработка результатов происходит в стандартной области, а это позволяет в полной мере использовать сильные стороны робастного планирования и регрессионного анализа. При этом возникает необходимость в специальных средствах для преобразования произвольной области в стандартную и обратного перехода при проведении вычислительного эксперимента. Рассмотрим более подробно, как осуществляется преобразование области планирования.
Особенность областей с ограничениями в том, что интервал изменения (или конкретное значение) одной или нескольких переменных зависит от значения, принимаемого другой переменной, или от сочетания значений нескольких переменных. Для преобразования области, переменные, которые зависят от других, должны быть заменены фиктивными, являющимися независимыми друг от друга. За уровни варьирования фиктивных переменных обычно принимают условные значения типа 0, 1, 2 и т.д. Фиктивная переменная вводится таким образом, чтобы она была ортогональной ко всем остальным[7]. Затем определяется функция Хiф = f(Xзакор, Xi).
Для качественной аппроксимации связей между фиктивными и действительными факторами можно использовать полиномы Чебышева. Для получения такой зависимости составляется матрица плана полного факторного эксперимента (полного перебора всех вариантов сочетаний значений уровней факторов). В качестве факторов в эту матрицу входят фиктивная переменная и все переменные, от которых зависит натуральная переменная, вместо которой введена данная фиктивная. Откликом являются значения натуральной переменной, принимаемые ею при данном сочетании влияющих факторов.
Посредством процедуры регрессионного анализа мы можем получить модель наперед заданной точности для описания связей между натуральной и фиктивной переменной. В дальнейшем выбор плана происходит как в стандартной ситуации. При проведении экспериментов, в рабочую матрицу вместо фиктивных значений записываются натуральные. При получении модели, в матрице оперируют с фиктивными переменными. Затем для вычислительного эксперимента вместо фиктивных переменных подставляют их выражения, полученные из зависимостей. В случаях, когда зависимость в явной форме получить нельзя, приходится для каждого набора конкретных значений переменных вычислять соответствующее значение фиктивной переменной из уравнения или системы уравнений. Недостатком способа является то, что при росте числа зависимых факторов (больше 3) и при увеличении сложности области для обеспечения высокой точности требуется все больше точек, что не всегда достижимо. Тем не менее, этот способ наиболее корректно решает поставленную задачу.
6.3.6. Использование переменных, измеряемых в шкале наименований
Практически в каждой задаче среди независимых переменных присутствуют переменные, измеряемые в шкале наименований, или так называемые «качественные» факторы (марка материала, наименование оборудования, способ лечения, тяжесть заболевания, пол и т.д.). Часто можно встретить рекомендации по особым процедурам их обработки. В.П. Трофимовым [38] доказано, что применение специальных методов для этого не требуется. Построение регрессионной модели с «качественными» факторами математически не отличается от таковой с наличием только количественных переменных. При введении «качественной» переменной в план, нужно быть уверенным, что влияние каждого ее уровня (наименования) отличается только по силе влияния на зависимую переменную (отклик), а не по характеру (см. 6.5.3).
Если это условие не будет выполнено, то возможны два варианта развития событий:
- Влияния разных уровней «качественного» фактора могут взаимно компенсироваться, и в результате он не буде включен в структуру получаемой регрессионной модели, а его влияние будет считаться статистически незначимым. На самом деле, он может оказывать значимое влияние.
- Может оказаться, что влияние разных уровней настолько отличается друг от друга, что получить удовлетворительную модель не удастся. Удаление отдельных наблюдений приводит к полному изменению структуры модели. Иногда говорят: «модель рассыпается» и «собрать» ее не удается. Это означает, что нарушена непрерывность факторного пространства (см. 6.5.3).
В вышеописанных ситуациях для каждого уровня «качественного» фактора следует строить свою модель. При планируемом эксперименте такие ситуации можно предусмотреть, используя всю имеющуюся информацию. Помните, что «потом» практически ничего нельзя исправить.
Кроме того, при анализе модели и проведении вычислительного эксперимента следует всегда помнить о природе «качественных» переменных, для которых не существует никаких промежуточных значений, а только использованные в эксперименте.
В ситуации, когда число уровней значения переменной больше двух, значимость можно изучать применительно к отдельным точкам или областям (для двух уровней наличие значимого коэффициента регрессии и есть ответом на этот вопрос). В первом случае рассчитываются значения для конкретных наборов переменных при разных уровнях и доверительные интервалы для этих точек. Во втором случае строятся частные уравнения регрессии и доверительные области.
6.3.7. Эксперименты, в которых присутствует «состав»
Довольно часто исследователям приходится сталкиваться с задачами, в которых группа независимых переменных представляет собой «состав» (например, «состав» компонентов лекарственного препарата). Особенность такого набора факторов в том, что сумма компонентов в любом эксперименте равна 100%, что вводит линейную зависимость между переменными. Обычно предлагается использовать специальные планы на симплексе и полиномы Шеффе. Такие планы не являются робастными и требуют специальных методов обработки.
Как в такой ситуации простроить робастный план? Есть два пути.
- Можно воспользоваться многофакторным регулярным планом (см. приложение Г или каталог многофакторных регулярных планов Бродского В.З [5], а способ построения описан в начале этого раздела), но при этом придется выбросить один из компонентов. В этом случае вы получаете робастный план, но один компонент в модели будет отсутствовать (значение его всегда можно вычислить для любого сочетания других компонентов, поскольку сумма всех компонентов должна быть равна 100%).
- Если необходимо, чтобы в модели одновременно присутствовали все компоненты, следует строить специальный план эксперимента (к которым относится ранее упомянутый план Шеффе, не являющийся робастным, но включающий все компоненты). В таком случае нужно использовать функцию генерации плана ПС ПРИАМ, где предусмотрена такая возможность. Построенный таким образом план включает все факторы «состава» и при необходимости возможно включение дополнительно конструкционных, технологических и других факторов. В фармакологических задачах дополнительными факторами могут быть: доза препарата, время введения, способ введения и др. Необходимо следить за тем, чтобы число экспериментов не было слишком мало. Желательно, чтобы оно было равно 2 в целой степени, но не меньше определенного в (6.8). Качество такого плана несколько хуже, так как он скорее квазиробастный, чем робастный, поскольку в нем существуют связи между факторами. Тем не менее при решении сложных задач ему следует отдать предпочтение, особенно когда кроме компонентов «состава» присутствуют другие факторы, например, технологические.
6.4. Проведение эксперимента
Знания, не рожденные опытом, матерью всякой достоверности, бесплодны и полны ошибок.
Леонардо да Винчи
6.1.4. Общие требования
Среди всего другого ничто так не содействует победе как точное выполнение подаваемых сигналов
Вегеций, «Краткое изложение основ военного дела»
Качество итоговых результатов и выводов при использовании статистических методов, в том числе и теории планирования эксперимента, зависит от качества первичной информации. Поэтому необходимо тщательно выполнить все требования проведения многофакторного эксперимента, которые сводятся, в основном, к следующему:
- Исключение систематических ошибок.
- Проведение опытов строго в соответствии с разработанным планом и методикой проведения эксперимента.
- Проведение повторных опытов в номинально одинаковых условиях. Они нужны для расчета дисперсии воспроизводимости, которая используется для оценок адекватности полученной модели, и определения значимости коэффициентов регрессии. Кроме того, проведение повторных опытов позволяет проанализировать аномальные наблюдения, которые могут существенно исказить результаты моделирования. Чем больше число параллельных опытов, тем больше точность эксперимента. Однако, увеличение числа параллельных опытов (больше 3 — 4) не дает значительного эффекта. Дублирование может выполняться в одной точке (выбирается центр плана), в нескольких точках и во всех точках плана. В последнем случае получаются наилучшие результаты. Иногда дисперсию воспроизводимости получают из отдельной серии опытов, не входящих в план.
- Одной из распространенных ошибок является использование результатов не повторных опытов, а повторных измерений. Это недопустимо. Дело в том, что использование повторных измерений означает, что мы учитываем только ошибку измерения, которая является только частью (обычно незначительной) ошибки воспроизводимости. Неправильное определение дисперсии воспроизводимости приводит к неправильному определению структуры модели.
- Порядок проведения опытов должен быть рандомизирован, то есть опыты должны проводиться в случайном порядке. Это позволяет уменьшить систематические ошибки. При проведении экспериментов не в рандомизированном порядке очень часто происходит нарушение одной из предпосылок регрессионного анализа — независимости наблюдений. Это связано с тем, что для упрощения эксперимента часто удобно фиксировать все переменные и менять только одну. Такая организация эксперимента может привести к неправильной интерпретации результатов исследования и получению заниженной оценки дисперсии воспроизводимости, а также к автокорреляции ошибок наблюдений, что является нарушением одной из предпосылок регрессионного анализа.
В тех случаях, когда рандомизация невозможна в силу экономических, технических, организационных или каких-либо других причин, необходимо применять все меры для обеспечения независимости наблюдений. К таким мерам можно отнести «расстройку» установки или технологического процесса после каждого эксперимента и установление параметров функционирования заново и т.п.
- В эксперименте следует использовать материалы, лабораторных животных и пр., обладающие однородными свойствами. Если это невозможно, необходимо выделять источники неоднородностей.
- Все неизменяемые в эксперименте факторы должны быть зафиксированы на выбранных уровнях.
При построении модели по данным пассивного эксперимента и в случае насыщенного или сверхнасыщенного плана (в котором число опытов равно или меньше числа факторов) необходимо проводить контрольную серию опытов. Отсутствие контрольной выборки не позволяет надежно проверить предсказывающие свойства модели. Проведение контрольной серии экспериментов обязательно, если построенную математическую модель собираются использовать для предсказания.
6.4.2. Тактика проведения экспериментов при поиске оптимальных условий
Проведение экспериментов при поиске оптимальных условий имеет некоторые особенности.
После определения необходимого числа экспериментов (по табл. 6.1), исследователь проводит первую серию экспериментов по плану, сгенерированному на основе ЛПt-чисел или чисел Холтона. Опыты можно не дублировать. После проведения всей серии экспериментов определяется наилучшая (по выбранному критерию качества) точка. В случае нескольких критериев, для определения наилучшей точки воспользуйтесь функцией «Многокритериальная оптимизация«. Дальнейшие действия зависят от того, соответствует ли эта найденная точка поставленной цели или нет. В прикладных исследованиях это возможно, поскольку еще до начала исследований известно какая степень «приближения к глобальному экстремуму» нас устроит (например, снизить массу на 15% или увеличить выход годных изделий на 10% и т.п.).
Если полученная точка нас удовлетворяет, то в ее окрестности проводится проверочный эксперимент (3 — 4 опыта) и на этом работа заканчивается. Когда же в процессе проверочного эксперимента обнаруживают сильное расхождения (разумеется, в сторону ухудшения показателей), то это значит, что результат был случайным (ведь повторных опытов не проводили!). В таком случае в экспериментальной выборке выбирают следующe. точкe и анализ проводят аналогичным образом. Если, точка нас не удовлетворяет, можно выбрать для продолжения работ один из следующих вариантов:
- Провести дополнительную серию экспериментов по всей области исследования.
- Провести дополнительную серию экспериментов в области предполагаемого существования оптимума.
- Построить по полученным данным математическую модель и найти область оптимума с помощью вычислительного эксперимента.
Выбор того или иного варианта осуществляется в зависимости от имеющихся в распоряжении ресурсов на дальнейшее проведение экспериментов и результатов, достигнутых после первой серии.
Вариант 1 выбирается, если наилучшая полученная точка, по мнению исследователя, находится слишком далеко от области оптимума.
Вариант 2 предполагает, что найденная наилучшая точка находится в области оптимума. В этом случае новые эксперименты ставятся в некоторой ее окрестности, что достигается соответствующим изменением границ переменных. Число опытов при этом в 2 — 4 раза меньше, чем в первой серии.
Вариант 3 выбирается, когда дальнейшие эксперименты проводить невозможно или экономически невыгодно, при этом число факторов (независимых переменных) по сравнению с числом опытов относительно невелико.
6.4.3. Пассивный эксперимент
…мало-помалу Мордона начал побирать черт, ибо стало ему проясняться, что вся эта вполне правдивая и во всех отношениях осмысленная информация ему совершенно не нужна, ведь она превращалась в ужасную смесь, от которой разламывалась голова и подгибались ноги.
С. Лем, «Путешествие шестое, или как Трурль и Клапауций демона второго рода создали, дабы разбойника Мордона одолеть».
В философии? в теории познания (как и в большинстве естественных наук) разделяют наблюдение и эксперимент. При этом под экспериментом понимают такое познание, при котором исследователь может активно воздействовать на изучаемое явления или процесс. Поскольку в теории планирования эксперимента (ТПЭ) несколько иная терминология, это во многих случаях вызывает путаницу. В ТПЭ под экспериментом понимаются любые данные, которые подлежат обработке с целью построения математической модели, независимо от источника и способа получения этих данных. При этом различают активный и пассивный эксперимент. Активный эксперимент — это такой эксперимент, матрица условий проведения которого организована в соответствии с требованиями ТПЭ.
Пассивный эксперимент — эксперимент, матрица независимых переменных которого, с точки зрения статистических критериев была построена не оптимально. При этом не имеет значения, что с точки зрения исследователя построенный план эксперимента отвечает его представлениям об оптимальности (отличным от ТПЭ). Есть единственное исключение, довольно часто встречающееся при малом числе факторов: случай полного факторного эксперимента, который представляет собой полный перебор всех вариантов сочетаний уровней факторов.
Пассивный эксперимент по качеству исходного материала существенно уступает активному. Результат его очень сложно обрабатывать, а качество полученной модели практически всегда не очень высоко, особенно для показателей информативности, устойчивости и предсказующим свойствам.
При пассивном эксперименте перед получением модели следует выполнить следующие действия:
- Разделить всю выборку на однородные подвыборки.
- Каждую однородную подвыборку разделить на обучающую и контрольную подвыборки.
- В каждой однородной подвыборке построить по обучающей последовательности опытов свою модель и проверить ее по контрольной последовательности.
Необходимость разделения на однородные подвыборки разъясняется в 6.3.6. При формировании обучающей выборки следует попытаться получить матрицы с минимально закоррелированными столбцами.
Считаем необходимым предостеречь против самой худшей формы пассивного эксперимента, которая, к сожалению, является очень распространенной: когда результаты эксперимента и значения независимых переменных снимаются непосредственно с действующего в установившемся режиме эксплуатации технологического процесса.
Попытка получения информации таким образом заранее обречена на неудачу (за исключением случаев, когда технологический процесс сильно «расстроен»).
Основная причина этого в том, что любой технологический процесс функционирует в некоторой квазистационарной области: интервалы изменения независимых переменных (параметров управления процессом) выбраны таким образом, что бы их изменение существенно не влияло на отклик. Поэтому при обычном функционировании технологического процесса на отклик в основном влияют (в смысле отклонение от среднего) случайные факторы. Таким образом, получение полезной информации из такого эксперимента, мягко говоря, маловероятно.
Кроме того, подобная ситуация осложняется еще одним обстоятельством: независимые переменные являются случайными величинами, что требует применения не регрессионного, а конфлюэнтного анализа, который менее разработан, требует дополнительных сведений и недостаточно надежен.
Не делайте таких «исследований»! Вы напрасно потратите время и деньги.
Исключением является ситуация, когда активный эксперимент невозможен в силу самой природы изучаемой системы. Это касается в основном экономических, социальных, экологических, биологических и других подобных систем. При их изучении следует особое внимание обращать на формирование выборки. Исходить при этом необходимо из цели исследования.
Выборка должна быть репрезентативной, то есть представлять генеральную совокупность изучаемого процесса, а не его особый фрагмент. Также должен быть обеспечен принцип объективности: из выборки не следует исключать наблюдения, кажущееся «неудобными», и выполнять другие подобные действия по подбору данных, которые заранее отвечают каким-то определенным выводам. В этом случае собранные данные обязательно следует проверять на неразрывность области.
Полученную однородную выборку необходимо разделить на обучающую и контрольную, которая затем будет использована для проверки полученной модели. Желательно также попытаться так организовать данные, чтобы главные эффекты и взаимодействия для обучающей выборки были как можно менее закоррелированы друг с другом. Это означает, что экспериментальные точки должны быть равномерно распределены по факторному пространству. При небольшом количестве факторов это можно определить визуально — по диаграммам рассеивания (рис. 4.1 — 4.5 представляют собой диаграммы рассеивания для двух переменных). В идеальном случае диаграмма рассеивания должна иметь вид, представленный на рис. 6.6 или 6.8.
Для пассивного эксперимента, данные которого образованы сбором информации, характерны высокая закоррелированность столбцов эффектов и одновременное наличие в матрице эксперимента факторов, которые физически очень зависят друг от друга (см. 4.1). Поэтому желательно предварительно произвести анализ множества факторов и включить в матрицу только независимые между собой и влияющие на данный отклик факторы. Для выделения таких факторов можно воспользоваться диаграммами «причина-результат».
После построение модели следует обратить внимание на анализ мультиколлинеарности (см. 6.7.3), который позволит правильно оценить качество модели, и проверить ее на контрольной последовательности опытов.
6.5. Предварительный анализ результатов эксперимента
6.5.1. Анализ однородности дисперсий
После проведения экспериментов необходимо сделать предварительную обработку результатов. На этом этапе рассчитываются средние значения отклика и дисперсии по каждому опыту. После этого, используя критерий Кохрена, проверяют однородность дисперсий и рассчитывают дисперсию воспроизводимости. Значение критерия Кохрена рассчитывают по формуле
,
где S2max — максимальная из дисперсий; Si2 — дисперсии, рассчитанные в каждом эксперименте по повторным (дублирующим) опытам по формуле
,
где n — количество дублирований опытов; — среднее значение отклика в i-том опыте; Yij — значение отклика в i-ом опыте при j-ом повторении.
Результат сравнивают с табличным, и если G < Gтабл, a, n-1, N, то гипотеза об однородности принимается и дисперсия воспроизводимости рассчитывается по формуле
.
Особый интерес представляет ситуация, когда проверка по G-критерию показывает, что дисперсии опытов неоднородные. Что нужно делать в этом случае? Причиной неоднородности дисперсий могут быть или грубые ошибки в результатах эксперимента (так называемые «выбросы») или отличный от нормального закон распределения ошибок. Для того, чтобы определить, какая причина вызвала неоднородность, необходимо проанализировать значение отклика в эксперименте, в котором дисперсия наибольшая. Специалист должен решить, является ли причиной «выброс». Если это так, то этот эксперимент следует провести повторно для получения нормального результата. Если нет, значит закон распределения случайных ошибок не является нормальным или же является нормальным, но с так называемыми «тяжелыми хвостами». Очень часто такая ситуация наблюдается при проведении испытаний на прочность до разрушения.
В таком случае можно продолжать обработку как обычно, но при этом следует помнить, что пользоваться интервальными оценками (для коэффициентов, откликов и т.п.) нельзя[8]. Теоретически предполагается необходимость корректировки коэффициентов модели (например, используя метод наименьших модулей) в связи с отклонением закона распределения от нормального, но при решении практических задач такая необходимость возникает крайне редко. Если вы получили удовлетворяющую поставленным задачам модель (например, по описывающим и предсказующим свойствам), то в корректировке нет необходимости.
6.5.2. Определение уровня влияния «шума»
Перед тем как приступить к построению модели, желательно определить, возможно ли из полученных данных выделить какую-либо закономерность. Это можно формально определить, проверяя, принадлежат ли к одной генеральной совокупности дисперсия относительно общего среднего и дисперсия воспроизводимости:
,
где — общее среднее, то есть среднее всех средних по столбцу.
Положительный ответ на этот вопрос означает, что с заданной вероятностью в наших данных не содержится какой-либо закономерности. Причины могут быть следующими:
- уровень влияния неконтролируемых факторов очень высок, и на фоне их воздействия полезная информация не проявляется;
- неправильно выбраны независимые переменные, интервал или уровни их варьирования и на отклик они значимо не влияют (то есть или вы не включили в эксперимент часть значимо влияющих факторов, или же интервал изменения факторов в эксперименте слишком узок).
В такой ситуации хорошую модель, по объективным причинам, получить скорее всего не удастся. Поэтому необходимо проанализировать условия проведения эксперимента и саму формализацию. После чего следует либо провести новые исследования в измененных условиях, либо принять этот результат для учета факта отсутствия статистически значимой связи между независимыми переменными и откликом для использования в дальнейших практических действиях.
Как выполняются подобные проверки подробно описано в 3.2.
6.5.3. Анализ однородности (неразрывности) области эксперимента (кластерный анализ)
В регрессионном анализе постулируется, что гиперповерхность, описывающая поведение функции отклика в зависимости от выбранных независимых переменных, не имеет разрывов во всей области проведения эксперимента. Классическим примером такого разрыва является качественно разное влияние лекарственного препарата на организм (выздоровление или же ухудшение состояния) в зависимости от пола больного. Разрыв может возникать также при определенной комбинации некоторой совокупности независимых переменных. Необходимо понимать, что построить качественную и имеющую физический смысл модель для разрывной области невозможно по объективным причинам. В таких ситуациях должна быть построена модель для отдельных неразрывных подобластей. То есть, одна модель, например, описывает влияние препарата на организм мужчин, другая — на организм женщины и т.п. (см. 5.1).
6.6. Построение математических моделей по результатам эксперимента
Вселенная кажется… упорядоченной и задуманной в соответствии с числом…
Никомас из Герасы.
«Введение в арифметику»
6.6.1. Структура модели
Построение модели состоит из двух этапов: выбора структуры уравнения регрессии и получения оценок коэффициентов регрессии, а также их статистических характеристик.
Регрессионные модели обычно разделяют на две большие группы линейные и нелинейные по параметрам. К нелинейным, например, относится модель вида
Y = B1eB2X1 + B3eB4X2.
Матрицы, по которым строятся модели нелинейной регрессии, обычно плохо обусловлены, поэтому пользоваться ими следует исключительно в тех случаях, когда есть серьезные основания принять именно данный вид модели.
Линейность по параметрам не означает линейной зависимости. Зависимость может быть сколь угодно сложной. Линейность по параметрам лишь означает, что модель представляет собой алгебраическую сумму компонент, то есть , где fi(x1,x2, … xm) — произвольная функция от переменных (x1, x2, … xm).
Наиболее часто пользуются полиномиальной
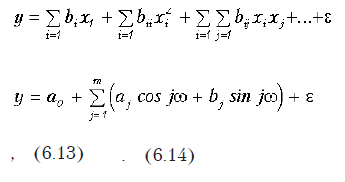
и рядами Фурье
В отдельный класс выделяют динамическую регрессию, в которой и сами коэффициенты модели зависят от времени.
При выборе структуры необходимо определить общую структуру (линейная или нелинейная регрессия, полином, ряд Фурье или что-либо другое), а затем — частную структуру, то есть конкретно, какие члены полинома или ряда Фурье должны войти в модель. Еще раз напоминаем: линейная регрессия означает лишь линейность вхождения членов, а сам член может иметь для полинома произвольный порядок.
Линейная по параметрам общая структура уравнения регрессии выбрана по следующим причинам:
- получение частной структуры для линейных моделей поддается автоматизации;
- возможно получение хорошо обусловленных матриц эксперимента;
- теоретически через k точек всегда можно провести полином степени не выше k-1;
- возможна компоновка отдельных членов модели функциями разного вида.
Задачу определения частного вида структуры в специальной литературе чаще всего называют «задачей выбора информативного подмножества эффектов», или «выбором наиболее значимых регрессоров». Следует отметить, что цели этих задач в общем случае не совпадают с задачей определения структуры и больше подходят под цели типа 3 (по [2]) — «задача правильного определения структуры модели, решение которой обеспечивает возможность количественного измерения эффекта воздействия на Y(X) каждой из объясняющих переменных в отдельности«. Тем не менее, на практике эти задачи (и цели) часто смешивают, что может привести к ошибочным результатам.
Проблемы выбора частной структуры (часто она называется «выбором наиболее информативного подмножества регрессоров») до настоящего времени теоретически не решена. Сложность в том, что при закоррелированности столбцов матрицы эксперимента различные статистические критерии становятся закоррелированы. При этом они уже не отражают истинного соотношения регрессоров и противоречат друг другу. Существуют десятки различных алгоритмов и подходов по определению структуры уравнения регрессии. По подходу их можно разделить на две большие группы:
- методы полного или частичного перебора, в которых анализируются модели в целом (например, МГУА);
- методы пошаговой регрессии, в которых модель формируется постепенным включением в нее (или исключением) по одному регрессору на каждом шаге работы.
Наибольшее внимания проблемам выделения существенных факторов и зависимости этого процесса от закоррелированности исходной матрицы уделили специалисты, разрабатывающие метод случайного баланса, который в настоящее время практически не применяется. Тем не менее, в виду того, что они должны были выделить именно настоящие факторы (иначе задача не имела бы решения) эти специалисты внесли значительный вклад в понимание данной проблемы. В ряде работ[9] предприняты попытки подвести теоретическое обоснование под метод случайного баланса и получить оценки качества плана эксперимента с точки зрения выделения всех значимых эффектов.
Так, в работе Мешалкина Л.Д. доказывается теорема Эдля для двухуровневых планов, согласно которой вероятность построения плана X, для которого можно выделить все значимые эффекты и получить их оценки, имеет значение не ниже, чем 1-2l, где l = I – K – log2(j – k + a), при этом К — число значимых эффектов; J — число подозреваемых эффектов; а I — число опытов.
В работе В.Д. Барского оценка качества плана определяется исходя из степени закоррелированости его столбцов. Оценкой качества служит вероятность того, что два значимых эффекта имеют коэффициенты парной корреляции по абсолютной величине больше a. Значение a принимается равным 0,3. Утверждается, что при значениях rij > a выделение эффектов невозможно (также невозможно разделить их влияние друг от друга). В работе Р.И. Слободчиковой утверждается, что a = 0,4.
Значительный интерес представляет изучение вопроса эффективности используемого алгоритма выделения существенных переменных. Этому посвящена работа З.С. Лапиной и Р.И. Слободчиковой, из которой взята табл. 6.5. Алгоритм применялся к группе специально созданных тестовых задач. Указывается, что на эффективность алгоритма влияют такие факторы, как крутизна спада вкладов, значимые факторы, закоррелированность матрицы плана, уровень ошибок воспроизводимости. Оценка влияния первых двух факторов в зависимости от изменения их значения не проводится. Относительно ошибки воспроизводимости указывается, что при 2–5% ошибки эффекта, мало отличающиеся от дву-, трехкратной ошибки, не выделяются или выделяются с большой погрешностью. Если ошибок больше 5%, алгоритм работает очень неэффективно. Отмечается, что эффекты, которые алгоритму не удается выделить, расположены (по значимости) равномерно среди общего числа значимых эффектов.
Таблица 6.5
Средний процент выделенных истинных эффектов
| Наличие ошибки измерения У | Закоррелированность | Наличие крутизны | Отсутствие крутизны |
| нет | |rij| = 0 | 100 | 80 |
| |rij| >=0 | 70 | 53 | |
| есть | |rij| = 0 | 93 | — |
| |rij| >=0 | 60 | — |
Можно утверждать, что правильность и качество построенной модели находятся в существенной зависимости от степени закоррелированности регрессоров, включенных в модель[10].
Формально уравнение регрессии у нас есть, но фактически оно непригодно к практическому применению. Даже применение расчетов с очень большим количеством значащих цифр не спасает положения. Единственный выход — применение методов регуляризации[11]. К сожалению выбор параметров в этих методах слабо формализован и параметры дают, хотя и устойчивую, но смещенную оценку. Поэтому желательно избегать ситуаций, которые требуют применения такого сложного математического аппарата.
Мультиколлинеарность — «почти» линейная зависимость строк матрицы линейной системы уравнений, вследствие чего система становится вырожденной или плохо обусловленной. В регрессионном анализе это матрица XTX. Мультиколлинеарной она становится в случае сильной закоррелированности столбцов матрицы эксперимента X. В связи с мультиколлинеарностью возникает ряд проблем при вычислении оценок коэффициентов регрессии.
В частности, дисперсии оценок коэффициентов регрессии становятся очень большими (а сами коэффициенты статистически незначимыми); построить доверительный интервал для каждой из них невозможно. Статистические оценки становятся закоррелированными и не отражают истинного соотношения между регрессорами, а также становятся неустойчивыми по отношению к малым изменениям в исходной выборке.
Кроме этих, достаточно неприятных последствий высокой закоррелированности существует еще один, не менее неприятный момент.
Оказывается, что при неправильном выборе частной функции регрессии оценки коэффициентов регрессии будут несмещенными, состоятельными и эффективными только при отсутствии закоррелированности (см. сноску на стр. ). Кроме того, вследствие закоррелированности оценок коэффициентов и их статистических характеристик в общем случае невозможно разделить влияние регрессоров.
В ряде работ отмечено, что уже при уровне парной корреляции 0,3 — 0,4 выделение истинных регрессоров становится невозможным.
На самом деле, ситуация, очевидно, несколько сложнее, так как степень относительной закоррелированности зависит не только от значения парной корреляции между двумя эффектами, но и от их корреляция со всеми остальными эффектами и с откликом.
Некоторые вычислительные эксперименты показали, что даже в сравнительно простых условиях (малое общее количество анализируемых регрессоров) закоррелированность снижает вероятность правильного выбора регрессоров.
Поскольку закоррелированность присуща не только пассивному эксперименту, но и активному (вследствие необходимости введения взаимодействий), задача определения частного вида структуры уравнения регрессии имеет большое практическое значение.
В общем случае при последовательной (пошаговой) процедуре определения структуры на каждом шаге выполняются следующие действия:
- Устанавливается регрессор, имеющий наибольшее влияние на отклик на данном шаге по заданному критерию (критериям).
- Производятся корректировки матрицы эксперимента, учитывающие включение выбранного регрессора.
- Проверяется окончание процесса выделения (если процесс не окончен, то возвращаемся в п. 1).
Структура модели однозначно определена только в том случае, когда все регрессоры в исходном множестве ортогональны друг другу. Такая ситуация возможна только для случая полного факторного эксперимента (ПФЭ), который в практической деятельности встречается крайне редко, ввиду огромных ресурсов, требуемых на его проведение (ПФЭ — фактически полный перебор всех вариантов). Возможность же получения различной структуры при изменении параметров вычислительного процесса противоречит интуитивному представлению пользователя и мнению философов о том, что модель является отражением некоторых объективно существующих закономерностей. Подробно с вопросами получения структуры можно ознакомиться в [14, 15].
Стремление к адекватности модели любой ценой обычно ведет к снижению информативности и ухудшению предсказывающих свойств. Предсказывающие и описывающие свойства находятся в противоречии друг с другом, то есть улучшение одного свойства ведет к ухудшению другого. Модель с наивысшими показателями информативности может быть неадекватной и с неудовлетворительными предсказывающими свойствами. Некоторые пользователи считают, что модель должна содержать только члены со статистически значимыми коэффициентами регрессии. При этом под статистической значимостью понимается их соответствие t‑критерию. Необходимо отметить, что корректное применение t-критерия возможно только при полностью ортогональной матрице, поэтому мы рекомендуем пользоваться им только при ПФЭ. Кроме того, при сложных экспериментах, при большом количестве регрессоров значимое влияние на отклик оказывает группа регрессоров, при том, что каждый из них формально статистически незначим. Обращаем ваше внимание на тот факт, что критерии, которые используются для анализа статистических свойств модели, могут противоречить друг другу. Увеличение коэффициента множественной корреляции часто приводит к снижению его значимости, поскольку в модель включаются статистически незначимые члены. Противоречие между критериями может наблюдаться даже в ПФЭ: можно получить адекватную модель и при этом в нее не будут включены все значимые с точки зрения t-критерия коэффициенты или наоборот — все значимые коэффициенты включены, но модель неадекватна.
6.6.2. Преобразование данных
Перед построением модели осуществляется этап преобразования исходной матрицы независимых переменных. Преобразования необходимы для:
- формирования модели, достаточно сложной для адекватного описания процесса или явления (ортогональные контрасты и взаимодействия);
- обеспечения устойчивости структуры и коэффициентов уравнения регрессии (ортогональные контрасты и нормировка);
- преобразование области эксперимента сложной формы к стандартному виду (см. 3.4);
- учета особенностей изменения факторов (например, логарифмирование и другие специальные преобразования).
К стандартным преобразованиям относят функции построения ортогональных контрастов, нормирование и построение взаимодействий.
Построение ортогональных полиномов Чебышева (главных эффектов)
Ортогональные контрасты представляют собой полиномы Чебышева первой, второй и т.д. степеней от исходного столбца. Степень не может быть выше, чем число уровней варьирования минус единица. Все образованные столбцы будут ортогональны друг другу. Ортогональность может быть нарушена, если уровни варьирования переменной размещены на числовой оси очень неравномерно — различаются на порядок и больше. В этом случае между переменной xi и откликом имеется логарифмическая зависимость, необходимо произвести замену x`I = ln xi. В дальнейшем при стандартных преобразованиях для этой переменной следует строить ортогональный контраст только первой степени. Если же не будет осуществляться преобразование к ортогональным контрастам, а будет строиться матрица x, x2, x3 и т.д., то столбцы такой матрицы будут сильно закоррелированны. Более того, это так называемая матрица Гильберта, которая с ростом степени быстро становится плохо обусловленной, а затем и вырожденной (со степени 8), независимо от того, как выбран начальный столбец.
Полиномы Чебышева в общем виде представляются как полиномиальные функции от уровней варьирования исходных факторов:
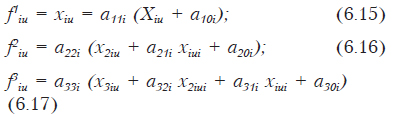
и т. д.
Здесь i — номер фактора, u — номер опыта, Xiu — исходные значения уровней варьирования.
Значения коэффициентов находят из условий
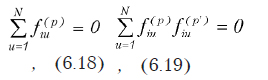
где fрiu и fр‘iu — ортогональные контрасты степени p и p’ для фактора Xi.
Подставляя выражения для ортогональных контрастов в соответствующие формулы можно получить системы линейных уравнений, корни которых и будут представлять искомые коэффициенты ортогональных полиномов Чебышева.
Для полиномов первой и второй степени эти корни рассчитываются по следующим формулам:
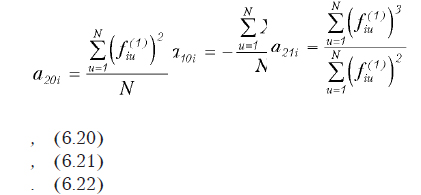
где a11i, a22i, a33i устанавливаются таким образом, чтобы рассчитанные значения полиномов Чебышева изменялись в интервале (–1, 1).
Нормировка
Для того, чтобы достичь хорошей обусловленности, одной ортогональности недостаточно. Если значения переменных значительно отличаются друг от друга, то это может привести к ошибкам, так как при этом ухудшается обусловленность матрицы и при вычислительных процедурах могут накапливаться ошибки. Поэтому мы настоятельно рекомендуем всегда выполнять ортогонализацию и нормировку исходной матрицы. Нормировки следует выполнять таким образом, чтобы сумма квадратов по каждому столбцу равнялась числу опытов:
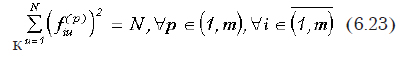
Построение взаимодействий
Еще одной стандартной операцией является построение взаимодействий. Физический смысл взаимодействия состоит в том, что изменение отклика вызывается одновременным изменением двух или большего числа факторов, а не изменением каждого из них в отдельности. Не нужно путать взаимодействие с взаимовлиянием факторов. Взаимовлияние — это влияние одного фактора на другой, а взаимодействие — совместное влияние нескольких факторов на отклик. Именно взаимодействия выявляют то, что является собственно свойствами системы, которые не выводятся непосредственно из свойств составляющих ее элементов (например, эффект потенцирования). Строят взаимодействия путем перемножения соответствующих столбцов. Обычно достаточно двойных взаимодействий, поскольку считается, что чем сложнее взаимодействие, тем меньше вероятность его значимого влияния на отклик. Тем не менее, могут быть процессы, где такие взаимодействия имеют место и их необходимо строить. Для полного факторного эксперимента необходимо строить все возможные классы, то есть в матрице должны быть взаимодействия от двойных до представляющих собой перемножение m столбцов ортогональных контрастов, где m — число исходных факторов. Для матрицы ПФЭ при невыполнении этого условия попытка построить информативную и адекватную математическую модель может быть неудачной.
Специальные преобразования
Кроме перечисленных выше общих преобразований достаточно часто могут выполнятся специальные преобразования, которые связаны с особенностями конкретной задачи. Они должны выполняться до стандартных преобразований. Наиболее часто используют следующие преобразования:
- Преобразования для приведения области планирования к стандартному виду (см. 6.3.5).
- Логарифмирование отдельной переменной Xi. Такое преобразование выполняется в том случае, когда интервал изменения переменной очень большой (наименьшее значение в 10 и более раз меньше наибольшего). Такой интервал предполагает логарифмическую зависимость отклика от Xi . Поэтому переменную необходимо прологарифмировать, а в дальнейшем строить от нее только ортогональный полином первой степени. Например, в фармакологических исследованиях в качестве такого фактора часто выступает время.
6.6.3. Получение коэффициентов математической модели и их статистических характеристик
Расчет коэффициентов математической модели основывается на применении метода наименьших квадратов (МНК) (см. 6.1).
Индивидуальные доверительные интервалы для коэффициентов регрессии определяются по формуле
![]()
где s — среднее квадратическое отклонение (корень квадратный из дисперсии воспроизводимости), cii — диагональный коэффициент матрицы дисперсий-ковариаций, то есть матрицы (XTX)-1, которая образуется в процессе решения системы уравнений, tµ,n — табличное значение критерия Стьюдента с уровнем значимости µ, и n степенями свободы. При этом n = N(n-1) для случая, когда в каждом эксперименте имеется n повторов и n = n-1, когда дисперсия воспроизводимости вычисляется по n отдельным опытам.
Для более точного определения положения вектора истинных значений коэффициентов регрессии используют совместную доверительную область или интервалы Бонферрони. Доверительные интервалы можно рассчитывать только когда ошибки распределены по нормальному закону. В практических работах анализ доверительных интервалов почти никогда не производят. Это связано с тем, что если модель обладает удовлетворительными свойствами по описанию исследуемого объекта, остальные ее характеристики оказываются менее значимыми.
Необходимо помнить, что величина коэффициента корреляции может служить характеристикой его значимости относительно других коэффициентов только в случае ортонормированной матрицы. При наличии мультиколлинеарности еще требуется и правильное определение структуры уравнения регрессии, поскольку величина коэффициента зависит от последовательности включения регрессоров в модель. Знак коэффициента регрессии однозначно говорит о направлении силы влияния только натуральной переменной для случая линейных эффектов (членов первой степени). Во всех остальных случаях необходимо анализировать эту зависимость, например, с помощью графиков частных уравнений регрессии.
Обычно для проверки значимости коэффициента регрессии используют значения t, долю участия, значение F для включения и некоторые другие критерии.
Критерий Стьюдента часто используют и для проверки значимости коэффициентов регрессии. В этом случае рассчитывается
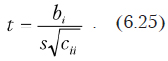
Если t > tµ,n, то коэффициент значим, если наоборот — незначим. Строго говоря, обосновано пользоваться этим критерием можно только для случая полного факторного эксперимента, когда все столбцы матрицы эксперимента ортогональны между собой. В остальных случаях t не дает правильного представления о значимости коэффициента.
Доля участия — показатель, являющийся долей от общей суммы квадратов, которую объясняет данный регрессор.
Иногда используют b-коэффициент, b = bi.(Sxi/Sy). Он показывает насколько изменяется значение отклика при изменении данного регрессора на величину его среднеквадратического отклонения.
Следует иметь в виду, что все перечисленные показатели (коэффициент корреляции, доля участия, значение t, значение F для включения и пр.) согласованы между собой только в случае полной ортогональности матрицы, по которой вычисляются коэффициенты регрессии. Во всех остальных случаях они могут противоречить друг другу, что может служить косвенным признаком неправильного определения структуры модели.
Названные показатели могут также противоречить показателям адекватности и информативности. Причем это противоречие может наблюдаться даже для ПФЭ: включение новых, формально значимых членов в модель ведет к снижению информативности; модель уже адекватна, но существуют формально значимые члены, не включенные в нее; все значимые члены включены в модель, но она неадекватна.
6.6.4. Основные характеристики
Для принятия решения о границах применяемой модели следует произвести анализ ее свойств. Основными показателями качества модели являются:
- информативность;
- адекватность;
- устойчивость (коэффициентов регрессии и структуры модели);
- описывающие свойства модели;
- предсказывающие свойства модели;
- отражение структуры связей между факторами и откликом.
Рассмотрим перечисленные показатели более подробно. Информативность модели оценивается по величине коэффициента множественной корреляции и величине расчетного значения F-отношения для коэффициента корреляции. Обе величины должны быть как можно большими: желательно, чтобы значение множественной корреляции было от 0,95 и выше, а значение F-отношения — по крайней мере на порядок больше табличного (при этом параметр g для критерия Бокса—Веца должен быть 2 — 3 и выше). Неинформативность или низкая информативность может быть вызвана следующими причинами:
- неправильный выбор структуры уравнения регрессии ;
- неправильный выбор числа уровней варьирования (их слишком мало);
- диапазоны изменения переменных слишком узкие ;
- в план и эксперимент включены не все значимо влияющие факторы;
- на анализируемый отклик слишком большое влияние оказывают «шумовые» (неуправляемые, неконтролируемые) эффекты.
Неинформативную модель использовать нельзя.
Адекватность формально проверяется сравнением расчетного и табличного критерия Фишера (первое должно быть больше единицы, но меньше второго). Адекватную модель можно использовать, а неадекватную нельзя. Но из этого правила есть два исключения. Например, если модель адекватна, но неинформативна, это означает, что «шумовой» фон влияет на отклик значительно сильнее совокупности выбранных эффектов, и пользоваться моделью нельзя. Нередки ситуации, когда модель формально неадекватна, но по своим описывающим, предсказующим и информативным свойствам полностью удовлетворяет поставленным прикладным целям. Такую модель можно использовать в прикладных исследованиях. Это решение основывается на том, что проверка F-критерия является только формальной проверкой одного из свойств модели. Адекватность же в математическом моделировании означает отражение моделью с заданной точностью определенной совокупности свойств объекта, что и выполняется в данном случае.
Для оценки устойчивости коэффициентов регрессии используют число обусловленности и таблицу мультиколлинеарности. Идеальное число обусловленности равно единице. Допускается его значение в несколько десятков (до 100). При очень больших значениях этого показателя матрица нормальных коэффициентов является плохо обусловленной, коэффициенты неустойчивы. При анализе таблицы мультиколлинеарности следует признать наличие сильной закоррелированности, если значение абсолютных величин коэффициентов парной корреляции между независимыми переменными больше 0,4 и значение коэффициентов парной корреляции между независимыми переменными значительно больше коэффициентов парной корреляции соответствующих переменных с откликом.
Наличие сильной мультиколлинеарности приводит к неустойчивости коэффициентов и резко снижает вероятность правильного определения структуры.
Описывающие свойства со статистической точки зрения характеризуются адекватностью модели, а с точки зрения пользователя — средним и максимальным процентом отклонения значений, рассчитанных по модели по отношению к экспериментальным. Следует помнить, что используемые процедуры обеспечивают минимизацию среднего, а не максимального отклонения. Кроме того, улучшение (формальное) описывающих свойств может привести к снижению информативности модели и ухудшению ее предсказывающих свойств. Поэтому, если модель адекватна (по F-критерию), то дальнейшее улучшение ее описывающих свойств приведет к указанным выше последствиям и будет противоестественным, так как мы получаем модель, которая дает как будто бы меньшее рассеивание, чем сам исследуемый процесс.
Предсказывающие свойства модели оцениваются путем сравнения значений, рассчитанных по модели, с экспериментальными для контрольной последовательности опытов, не совпадающей с выборкой, по которой построена модель. Показатели аналогичны показателям описывающих свойств для обучающей выборки.
Надежность модели с точки зрения правильности структуры связей между независимыми переменными и откликом можно оценить только косвенно по следующему набору признаков:
- структура модели не должна противоречить представлениям о природе процесса или явления;
- качество предсказывающих свойств модели не должно существенно отличаться от качества описывающих свойств, что проверяется по F-критерию (проверка на адекватность);
- мультиколлинеарность матрицы дисперсии-ковариаций должна быть умеренной (cond < 100);
- модель должна быть информативной.
Следует иметь ввиду, что модель может правильно, но неполно отражать структуру связей, даже при наличии неадекватности и неудовлетворительных описывающих и предсказывающих свойств.
Собственно анализ структуры связей производится по показателю «доля участия» из таблицы описания модели в кодированных переменных. Значение ее показывает долю общего рассеивания, объясняемую посредством конкретного регрессора. Фактически этот показатель отражает иерархию силы влияния на отклик эффектов, включенных в модель.
6.6.5. Действия при неудаче в построении математической модели
…и неуспех (опыта) обогащает человека новыми знаниями.
Френсис Бэкон
В ряде случаев построить удовлетворительную математическую модель не удается. Действия, которые можно предпринять в такой ситуации разделяют на две группы: 1) не требующие проведения новых экспериментов; 2) требующие проведения дополнительных экспериментов.
К первой группе относятся:
- повышение степеней ортогональных контрастов всех факторов до максимально возможных (число уровней минус 1);
- построение взаимодействий всех возможных классов;
- ослабление требований к регрессорам, допускаемым к проверке на включение в модель (снижение минимального коэффициента корреляции с откликом и минимальной доли участия, увеличение закоррелированности между эффектами).
Следует помнить, что эти действия, обеспечив получение формально адекватной модели с удовлетворительными описательными свойствами, могут привести к ее переусложнению и снижению устойчивости. В связи с этим качество полученной модели необходимо тщательно анализировать.
Возможны следующие причины, по которым модель получается неадекватной:
- неоднородность (разрывистость) области эксперимента;
- невключение в план эксперимента факторов, имеющих значительное влияние на отклик;
- узкие диапазоны изменения факторов, при изменении внутри которых он не оказывает существенного влияния на зависимую переменную;
- недостаточное число уровней варьирования;
- ошибки в проведении эксперимента (неточные установки уровней варьирования, отсутствие соблюдения неизменяемости зафиксированных факторов, существенное влияние контролируемых неуправляемых факторов).
Устранение этих причин требует проведения дополнительных исследований.
6.7. Анализ качества модели
Satius est bene ignorabe, quam malt didicisse[12].
Вы же знаете этих непосвященных, которые с трудом различают крупную дипломатическую победу и тяжкое дипломатическое поражение.
Кейт Лаумер, «Мирный посредник»
В сложных ситуациях оценки качества модели с помощью одного или двух свойств недостаточно — необходима комплексная оценка, позволяющая оценить статистические и потребительские свойства модели в полном объеме. Обязательно следует проверить информативность, адекватность и устойчивость модели. Желательно также анализировать предсказывающие свойства.
При анализе каечства используются некоторые дисперсии. В табл. 6.6 приведены расчетные формулы и названия дисперсий.
Таблица 6.6
Дисперсии, используемые в регрессионном анализе
| Название дисперсии | Расчетная формула |
| Дисперсия воспроизводимости[13] S2воспр | |
| Остаточная дисперсия S2ост | |
| Общая дисперсия (дисперсия относительно общего среднего) S2 | |
| Дисперсия, объясняемая моделью S2R |
где N — число опытов; k — число членов модели; n — число дублирующих опытов в каждом эксперименте; Yij — значение отклика в i-ом эксперименте при j-ом повторе; — среднее значение по повторным опытам в i-ом эксперименте; — значение отклика, рассчитанное для i-го эксперимента по модели; — общее среднее.
6.7.1. Информативность
Наиболее часто оценкой информативности служит величина множественного коэффициента корреляции R (коэффициент корреляции между экспериментальным значением отклика и значением отклика, рассчитанным по модели). Чем ближе он к единице, тем выше информативность модели. Величина R2 представляет собой долю общей суммы квадратов, объясняемой моделью:
![]()
Его значение должно быть как можно ближе к единице. Эмпирически установлено, что для активного эксперимента оно должно быть не менее 0,96 — 0,97. Это необходимое, но недостаточное условие. Достаточным условием является проверка значимости коэффициента множественной корреляции по критерию Фишера:
![]()
где VR, Vост — степени свободы для дисперсии, объясняемой моделью и остаточной дисперсией соответственно.
Если расчетное значение больше табличного с заданным уровнем значимости, то модель информативна. Такая проверка информативности является качественной. Для того, чтобы оценить уровень информативности количественно, можно воспользоваться критерием Бокса — Веца. Хорошая модель должна иметь параметр g критерия Бокса — Веца не ниже, чем 2 — 3. g определяется из уравнения
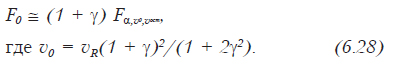
Если определить g по этой формуле невозможно, то приближенно значению g = 3 соответствует ситуация, когда Fрасч »10Fтабл.
6.7.2. Адекватность
В широком смысле под адекватностью понимается соответствие модели описываемому процессу или объекту по заранее определенным условиям. В узком смысле в регрессионном анализе проверка адекватности сводится к проверке по критерию Фишера принадлежности дисперсии воспроизводимости и остаточной дисперсии к одной генеральной совокупности. При положительном ответе (F-табличное меньше F-расчетного) модель считается адекватной с заданным уровнем значимости, при этом различие дисперсий статистически незначимо.
Обращаем ваше внимание: проверка эта является формальной, поэтому окончательное решение об адекватности модели следует принимать, исходя из пригодности модели к практическому применению по всей совокупности параметров. То есть формально модель может быть неадекватной, а для пользователя, с прикладной точки зрения, процесс описывается адекватно (структура связей, точность описания или предсказания и пр.).
При наличии повторных опытов адекватность модели проверяется по критерию Фишера:
![]()
В том случае, когда повторные опыты отсутствуют, модель считается адекватной, если выполняется условие[14]
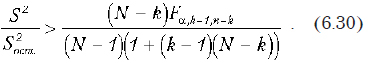
Следует иметь в виду, что эта формула не может дать информацию для принятия решения о прекращении включения регрессоров в модель и об адекватности самой модели. Необходимо провести смысловой анализ и возможно выполнить следующие действия.
- Проанализировать диаграмму влияния регрессоров (см. 6.7.5).
- Проанализировать характер изменения значений S2ост от включения новых членов в модель. Если остаточная дисперсия начинает увеличиваться, то добавление новых членов в модель следует прекратить.
- Проанализировать изменения FR при включении новых членов и остановится на модели с его максимальным значением.
После того, как модель стала адекватной по F-критерию, не следует включать в нее дополнительные члены, так как они не несут никакой дополнительной информации и это приводит к снижению или даже потере информативности (уменьшается FR). Результаты эксперимента и расчетные значения по адекватной модели статистически неразличимы, то есть не зная источника результатов, определить его по самим данным невозможно.
Расчетное значение F-критерия всегда должно быть больше единицы (то есть это отношение большей дисперсии к меньшей). В том случае, если оно оказалось меньше единицы его необходимо пересчитать. Не следует забывать при этом, что для табличного значения F-критерия числа степеней свободы V1 и V2 поменяются местами и само значение будет другим.
6.7.3. Устойчивость
Чем больше считаешь, тем больше запутываешься.
Тамильская пословица
Лучше никакого совета, чем плохой.
Норвежская пословица
В регрессионном анализе можно говорить об устойчивости в двух смыслах:
- устойчивость структуры уравнения регрессии;
- устойчивость оценок коэффициентов регрессии.
Обе устойчивости напрямую зависят от качества матрицы эксперимента и алгоритмов обработки данных. Непосредственно устойчивость в ПС ПРИАМ не проверяется, т.к. это требует проведения вычислительного эксперимента, требующего времени на порядок больше, чем само построение модели. Вместе с тем, выполняется расчет ряда косвенных критериев, которые позволяют с большей уверенностью судить об устойчивости структуры и оценок коэффициентов.
При анализе устойчивости рассматривается таблица мультиколлинеарности и число обусловленности. Таблица мультиколлинеарности содержит следующие столбцы: имена регрессоров, входящих в модель; максимальный по абсолютной величине коэффициент парной корреляции, который данный регрессор (его столбец) имеет с другими регрессорами, входящими в модель; имя этого регрессора; коэффициент корреляции с откликом. Эта таблица позволяет проанализировать устойчивость структуры уравнения регрессии.
Желательно, чтобы выполнялись следующие условия:
- максимальный коэффициент парной корреляции между регрессорами по абсолютной величине не должен превышать 0,3 — 0,4;
- коэффициент парной корреляции с откликом по абсолютной величине должен быть существенно больше, чем максимальный коэффициент корреляции с другим регрессором.
При выполнении этих условий можно быть уверенным в устойчивости структуры уравнений регрессии. Если второе условие не выполняется только для отдельных регрессоров, то вызывает сомнение правильность включения в модель именно этих регрессоров.
Рассмотрим в качестве примера табл. 6.7. Здесь регрессор х8 имеет коэффициент корреляции с регрессором х2 по абсолютной величине больший, чем его коэффициент корреляции с откликом (0,41 против 0,23). Такая ситуации вызывает сомнения относительно необходимость включения его в модель.
Таблица 6.7
Примерный вид таблицы мультиколлинеарности
| Имя регрессора | Максимальный коэффициент корреляции с другим регрессором | Имя регрессора, с который достигнут максимальный коэффициент корреляции | Коэффициент корреляции с откликом |
| х3 | 0 | со всеми | 0,79 |
| х2 | 0,045 | х8 | 0,45 |
| х1 | 0,12 | х3 | 0,38 |
| х8 | 0,41 | х2 | 0,23 |
Число обусловленности (cond) вычисляется как произведение норм прямой и обратной матриц нормальных уравнений[15] и показывает, во сколько раз может увеличиться относительная ошибка в коэффициентах при наличии ошибки в исходной матрице. По величине этого числа можно судить об устойчивости оценок коэффициентов регрессии. Теоретически наилучшим значением является cond = 1 (достижимо только для ортонормированной матрицы). При величине cond в десятки тысяч матрица практически является вырожденной. Если cond имеет значение в сотни и тысячи, то это повод для беспокойства относительно устойчивости оценок. Следует иметь в виду, что при этом статистические оценки закоррелированы и практически не несут никакой полезной информации.
ПОМНИТЕ! Робастный план, ортогонализация, нормировка снижают мультиколлинеарность и число обусловленности, они резко повышают устойчивость структуры модели и ее коэффициентов.
6.7.4. Описывающие и предсказывающие свойства
Статистической проверкой описывающих и предсказывающих свойств является проверка адекватности по обучающей и контрольной выборке соответственно.
Обычно адекватность модели оценивают по обучающей выборке. Желательно все же рассчитывать остаточную дисперсию по контрольной выборке, то есть специальной последовательности опытов, ни один опыт которой не совпадает с обучающей, но значения всех переменных лежат внутри интервалов, определенных по обучающей. Такая дисперсия называется «несмещенной оценкой остаточной дисперсии». После этого проверяется дисперсия (как описано ранее). Если контрольная выборка имеет повторные опыты, то и дисперсию воспроизводимости необходимо рассчитать по ней[16]. Если проверка подтверждает адекватность модели, то она обладает хорошими как описывающими, так и предсказующими свойствами[17].
Для практического применения эти свойства обычно оцениваются по среднему или максимальному проценту отклонения предсказанных по модели и экспериментальных значений. Для этого нужно просмотреть таблицу остатков. Следует помнить, что для хорошей модели все показатели по обучающей и контрольной выборке (то есть описывающие и предсказывающие свойства) должны быть близки. Если же предсказывающие свойства значительно хуже описывающих, это свидетельствует об ошибках в структуре модели. Наиболее часто это «перебор» — включение в модель избыточных членов, особенно высоких порядков. При проверке предсказывающих свойств необходимо следить, чтобы с одной стороны контрольная матрица не совпадала с обучающей, а с другой — все точки этой выборки должны находиться в пределах пространства, определенного обучающей выборкой.
Плохие предсказывающие свойства могут быть вызваны или неправильным выбором структуры в целом, или же тем, что структура усложнена за счет «балластных» эффектов. Эти эффекты можно обнаружить по диаграмме распределения силы влияния факторов. В такой ситуации необходимо повысить барьер для включения переменных в модель: для ПФЭ изменить уровень значимости, для других ситуаций увеличить значение доли участия.
Необходимо иметь в виду, что изменения описывающих и предсказывающих свойств находятся в сложной связи. При правильном подборе членов модели, то есть тех, которые соответствуют «истинной» структуре, сначала происходит улучшение как предсказывающих, так и описывающих свойств. Затем с некоторого момента улучшение описывающих свойств путем включения в модель новых членов ведет к ухудшению предсказывающих. Это или служит сигналом к прекращению увеличения сложности модели, или свидетельствует о неправильных критериях подбора членов модели. Бывают ситуации, когда эти свойства согласуются между собой только для самой простой модели, которая не удовлетворяет потребностям практического использования (она не «одинаково хорошо», а «одинаково плохо» описывает и предсказывает данные). Любые изменения в модели приводят к ухудшению предсказывающих свойств. Это указывает или на разрывность пространства, или же на то, что при формализации задачи в состав исследуемых не включены действительные факторы, влияющие на процесс, или же выбранные факторы не настоящие, а всего лишь отражения (проекции) неизвестных нам настоящих. Такая ситуация возникает, например, когда вместо анализа действительных факторов исследуют зависимость от времени.
6.7.5. Анализ структуры связей
Победа обычно достигается немногими
Вегеций,
«Краткое изложение основ военного дела»
Анализ структуры связей позволяет получить графическую иллюстрацию распределения силы влияния регрессоров на отклик. Сила влияния определяется как доля участия регрессора, рассчитываемая через отношение суммы квадратов, объясняемой данным регрессором, к общей сумме квадратов. Эта функция может применяться также и для анализа структуры. Для этого удобно выбрать изображение в виде столбиковых диаграмм. Нормальный вид распределения силы влияния представляет собой убывание по кривой, близкой по характеру к экспоненте (рис. 6.11). Если на диаграмме есть отклонение от убывания, то это может свидетельствовать об ошибке в определении структуры уравнения регрессии.
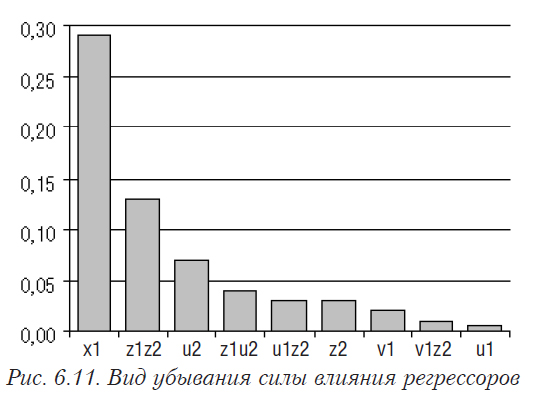
Наличие скачка, «обрыва» в распределении свидетельствует скорее всего о том, что следующие за «обрывом» регрессоры являются статистически незначимыми и включать их в модель не следует (рис. 6.12). Такое решение необходимо принимать только в том случае, если у вас нет достоверной оценки дисперсии воспроизводимости, полученной по экспериментальным данным. В этой ситуации эффекты, начиная с u1x2 (рис. 6.12), относятся к случайной составляющей и в модель не включаются.
Ситуация, изображенная на рис. 6.13 (отсутствие ниспадающей последовательности), означает, что в определении структуры присутствуют ошибки. Обычно это связано с закоррелированностью регрессоров. В этом случае различные критерии отбора значимости эффектов противоречат друг другу, и эффект, сильно влияющий по одному из критериев, согласно другому может влиять очень слабо. Кроме того, при закоррелированной матрице значения коэффициентов регрессии и всех их характеристик зависят от порядка (последовательности) включения регрессоров в модель. Если структура уравнения регрессии определена правильно, ситуации, изображенной на рис. 6.13, быть не должно.
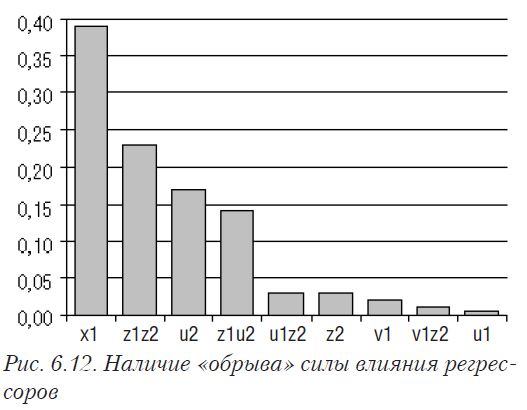
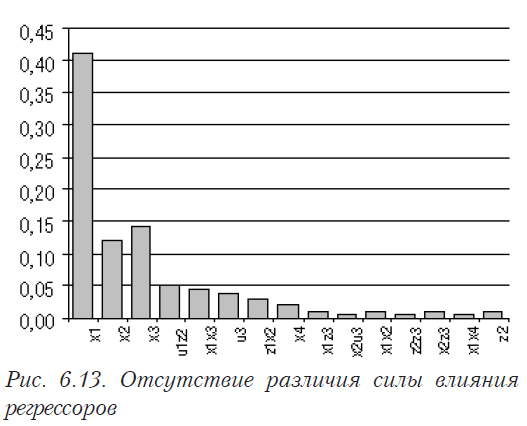
6.7.6. Анализ остатков
Остатки определяются как n разностей , i=1, 2,… n, где — прогнозируемая величина, получаемая при помощи найденного уравнения регрессии.
По сути это величины, которые нельзя объяснить с помощью регрессионного уравнения. При проведении регрессионного анализа делаются некоторые предположения относительно ошибок — ошибки независимы, имеют нулевые средние значения и постоянную дисперсию, подчиняются нормальному закону.
Если подбираемая модель правильна, то остатки будут проявлять тенденцию к подтверждению сделанных предположений или, по меньшей мере, не будут противоречить им.
После исследования остатков мы можем прийти к одному из выводов:
- предположения нарушены;
- предположения не нарушены.
Остатки исследуются с помощью графиков остатков. Основные из них:
- общий;
- в зависимости от времени, если известна последовательность реализаций опытов;
- в зависимости от предсказываемых значений Yi .
Если в графиках остатков обнаружено нарушение, это может означать либо действительное нарушение допущений регрессионного анализа, либо то, что частная структура уравнения выбрана неправильно.
Например, общий график остатков (рис. 6.14) выглядит следующим образом (правда, обычно в программах столбики диаграммы представлены пропорциональным количеством точек или звездочек):
Это свидетельствует о выполнении предпосылки о нормальности распределения остатков.
График временной последовательности позволит определять влияние эффекта времени на данные.
Если остатки «укладываются» в горизонтальную полосу, как это показано на рис. 6.15, то время не влияет на данные.
Наличие зависимости остатков от времени означает автокорреляцию остатков и нарушение одной из предпосылок регрессионного анализа, а именно — независимости остатков. При этом модель получается искаженной. Как предупредить такие ситуации см. 6.4. При получении области вида (рис. 6.16) необходимо применить взвешенный метод наименьших квадратов, так как в этом случае нарушена еще одна предпосылка — дисперсия ошибок непостоянна.
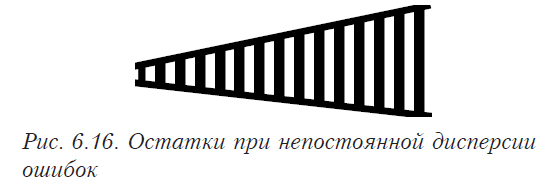
Области, показанные на рис. 6.17 и 6.18, означают, что структура модели неправильная, или нарушена предпосылка независимости ошибки от независимых переменных (линейные и нелинейные зависимости).
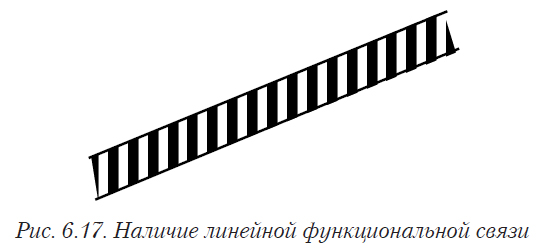
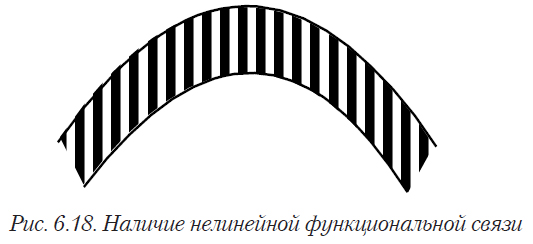
Наличие функциональной связи между остатком и величиной откликов может означать либо нарушение предпосылки о независимости дисперсии от откликов, либо наличие неправильной структуры модели. Во втором случае нужно попытаться получить модель с правильной структурой.
Графики остатков могут иметь и более сложную форму. Основное, что необходимо проверять на этих графиках, — наличие или отсутствие зависимости.
6.7.7. Анализ нарушений предпосылок и допущений регрессионного анализа
Всеобщий источник нашего несчастья в том, что мы верим, будто вещи действительно являются тем, чем мы их считаем.
Георг Кристоф Лихтенберг
Если все действия вы выполняете согласно описанной технологии, нарушений быть не должно.
Для строгой проверки наличия нарушений и их степени требуются вычислительные затраты, превышающие затраты на получение модели. При этом во многих случаях результаты этих проверок могут быть ненадежны. В связи с этим в соответствующих разделах приводятся признаки нарушений и процедуры для их исправления (см. 6.5, 6.7.3, 6.7.6). Рассмотрим следствия нарушений различных предпосылок.
Ошибки не распределены по нормальному закону
В этом случае кроме получения интервальных оценок для коэффициентов и отклика возможны различные проверки. Кроме того, проверка адекватности при отсутствии повторных опытов (и вследствие этого отсутствия дисперсии воспроизводимости) с использованием общей и остаточной дисперсий является неустойчивой. Формальные проверки нарушения нормальности практически невозможны в связи с необходимостью проведения большого количества дополнительных экспериментов (50 — 150). Проверка неформальная (см. 6.7.6). При явных и сильных нарушениях нормальности используют метод наименьших модулей, взвешенный метод наименьших квадратов, непараметрическую регрессию, оценки Хубера, Андрюса и пр. [29, 34]. Для одномерного случая можно использовать непараметрическую регрессию [32, 33].
Наличие мультиколлинеарности
Проблема сводится к невозможности выделения правильной структуры уравнения регрессии, неэффективности применения t- и F-критериев, неустойчивости оценок коэффициентов регрессии. Эффективных средств работы при наличии мультиколлинеарности не существует. Использование гребневой («ридж») регрессии приводит к получению устойчивых, но смещенных оценок. Проверка описана в 6.7.3.
Наличие ошибок независимых переменных
Проблема возникает, если независимые переменные имеют существенную случайную ошибку, соизмеримую с самой величиной переменной. То есть случайная ошибка может достигать такой величины, когда изменение значений существенно влияет на отклик.
При планируемом эксперименте возможна обработка и анализ результатов обычными методами. При пассивном эксперименте обработка требует сложного анализа и дополнительной информации. Такая обработка называется конфлюэнтным анализом и требует, по крайней мере, знания дисперсий этих ошибок.
Зависимость между ошибками
Наиболее частый вид такого нарушения называется автокорреляцией, когда каждое следующее по времени наблюдение зависит от предыдущих наблюдений. Они является или следствием неаккуратно проведенного эксперимента или же вызывается самой природой такого процесса (см. 6.4). При наличии автокорреляции необходима корректировка модели путем введения в нее дополнительного члена, учитывающего автокорреляцию.
Дисперсия ошибки не равна нулю.
Дисперсия ошибки переменная величина. Для такой ситуации используется частный случай обобщенного метода наименьших квадратов, который называется взвешенным методом наименьших квадратов. В этом методе коэффициенты находятся не из системы уравнений XTXВ = XTY, а из системы XTW-1XВ = XTW-1Y, где W — диагональная весовая матрица с элементами, равными оценкам дисперсий в точках эксперимента.
6.8. Программа преобразований исходных данных и предварительного формирования структуры уравнения регрессии
Поскольку программа «Регрессия» в Excel весьма слабая, был написан модуль преобразований исходной матрицы и предварительного отбора регрессоров для формирования структуры уравнения регрессии, текст которого приведен ниже.
Option Base 1
Type Rez_trans ‘Определение пользовательского типа
ort As Integer ‘флажок ортогонализации
pfe As Integer ‘флажок полного факторного эксперимента
inter As Integer ‘флажок построения взаимодействий
norm As Integer ‘флажок нормировки
End Type
Type MODPAR
cor_y As Double ‘ ограничен. min коэф. корреляции c y */
max_share As Double ‘ максимальная доля остатка при
‘ последовательном отборе кандидатов
End Type
Dim MP As MODPAR
Dim vid As Rez_trans ‘результаты преобразования исходной матрицы
Dim num_int As Integer ‘количество взаимодействий, определяемых пользователем
Dim num_factor As Integer ‘количество независимых переменных
Dim num_rows As Integer ‘количество строк в матрице
Dim num_y_cols As Integer ‘количество повторных опытов
Dim x_data_CELL As Object ‘независимые переменные
Dim y_data_CELL As Object ‘зависимые переменные
Dim name_CELL As Object ‘имена независимых переменных (факторов)
Dim pfe As Integer
Dim dp() As Integer ‘массив степеней главных эффектов
Dim dpz() As Integer ‘массив степеней главных эффектов
Dim dpn() As Integer ‘скорректированный массив степеней главных эффектов
Dim agn() As Double ‘массив формул перехода
Dim X() As Double ‘вспомогательный массив
Dim X1() As Double ‘вспомогательный массив
Dim bk(10) As Double ‘вспомогательный массив
Dim s_error As Integer ‘Индикатор ошибки
Dim MEFF As Integer ‘сумма возможных степеней факторов
Dim max_deg As Integer ‘максимальная возможная степень фактора
Dim var_c, deg_c As Integer
Dim a(1 To 10, 1 To 10) As Double ‘вспомогательный массив
Dim xok() As Double ‘расширенная матрица
Dim num_xok_col As Integer
Dim kof_norm() As Double ‘коэффициенты нормировки
Dim kof_norm_mod() As Double ‘коэффициенты нормировки для модели
Dim Num_inef As Integer ‘количество генерируемых взаимодействий
Dim D_I() As Integer ‘вспомогательный массив
Dim a1() As Integer ‘вспомогательный массив
Dim a2() As Integer ‘вспомогательный массив
Dim ti() As Integer ‘массив для хранения типов взаимодействий
Dim mav() As Integer ‘вспомогательный массив
Dim Num_Ext_col As Integer ‘номер последнего столбца
‘расширенной матрицы эффектов
Dim MD As Integer ‘вспомагательная переменная
Dim cor_mat_y() As Double ‘массив коэффициентов коррелляции с откликом
Dim Y_mod() As Double
Dim listcandw() As Integer ‘список кандидатов в модель
Dim newcand As Integer ‘счетчик эффектов-кандидатов в модель
Dim Y_aver As Double, D_opyt As Double
Dim d_sum As Double ‘общая сумма квадратов отклонений
Dim mef() As String ‘массив имен главных эффектов
Dim texed As String ‘строка для временного хранения информации
Dim ly As Integer, lop As Integer ‘вспомагательные переменные
Dim cur_i As Integer ‘Глобальный счетчик
Sub Build_Reg_model()
‘Ввод ссылки на область независимых переменных
Set x_data_CELL = Application.InputBox( _
prompt:=»Выберите область независимых переменных (без заголовков)», _
Type:=8)
num_factor = x_data_CELL.Columns.Count
num_rows = x_data_CELL.Rows.Count
‘Определение рабочих массивов соответствующих размеров
ReDim dp(num_factor)
ReDim dpn(num_factor)
ReDim dpz(num_factor)
ReDim agn(1 To num_factor, 1 To 8, 1 To 9)
ReDim X(1 To num_rows)
ReDim X1(1 To num_rows)
‘Ввод ссылки на область зависимых переменных
Set y_data_CELL = Application.InputBox( _
prompt:=»Выберите область зависимых переменных (без заголовков)», _
Type:=8)
num_y_cols = y_data_CELL.Columns.Count
‘Ввод ссылки на наименования независимых перемнных
Set name_CELL = Application.InputBox( _
prompt:=»Выберите массив имен независимых переменных», _
Type:=8)
anal_X ‘анализ исходной матрицы независимых переменных
If s_error = -1 Then
MsgBox «Фатальная ошибка в данных:» _
& «Один столбец не меняется»
GoTo e_sub
End If
open_fil
ReDim xok(1 To num_rows, 1 To MEFF)
ReDim kof_norm(1 To MEFF)
ReDim D_I(1 To MEFF)
ReDim a1(1 To MEFF)
ReDim a2(1 To MEFF)
ReDim mav(1 To MEFF)
ReDim ti(1 To MEFF)
‘Расчет формул перехода от натуральных
‘значений факторов к кодированным
or_con_ft
Dim i As Integer, j As Integer
‘Нормировка кодированной матрицы данных
norm
vid.norm = 1
If num_factor > 1 Then vid.inter = 1
If num_factor <= 1 Then vid.inter = 0
ti(2) = 1 ‘включать двойные взаимодействия
calc_int
Num_Ext_col = MEFF
cret_int
‘формирование столбца средних значений матрицы откликов,
‘расчет дисперсии или запрос на ее ввод
ReDim Preserve xok(num_rows, Num_Ext_col + 1)
Dim s2 As Double, s1 As Double, D_tmp As Double
ReDim Y_mod(num_rows)
num_y_col = y_data_CELL.Columns.Count
Y_aver = 0
D_opyt = 0
For i = 1 To num_rows
s2 = 0
xok(i, Num_Ext_col + 1) = 0
For j = 1 To num_y_col
xok(i, Num_Ext_col + 1) = xok(i, Num_Ext_col + 1) + y_data_CELL.Cells(i, j)
s2 = s2 + y_data_CELL.Cells(i, j) ^ 2
Next j
s1 = xok(i, Num_Ext_col + 1)
xok(i, Num_Ext_col + 1) = xok(i, Num_Ext_col + 1) / num_y_col
If num_y_col <> 1 Then
D_opyt = D_opyt + (s2 — xok(i, Num_Ext_col + 1) * s1) / (num_y_col — 1)
End If
Y_aver = Y_aver + xok(i, Num_Ext_col + 1)
Next i
Y_aver = Y_aver / num_rows
B0 = Y_aver
‘ вычисление максимального отклонения от среднего значения
maxa = Abs(B0 — xok(1, Num_Ext_col + 1)) ‘ присвоение начального значения
ind = 1
For i = 1 To num_rows
Y_mod(i) = B0
s1 = Abs(B0 — xok(i, Num_Ext_col + 1))
If maxa < s1 Then
maxa = s1
ind = i ‘номер опыта с наибольшим отклонением
End If
Next i
s1 = 0
maxp = (B0 / 100) * maxa
d_sum = 0
For j = 1 To num_rows
‘ общая сумма квадратов отклонений
d_sum = d_sum + (xok(j, Num_Ext_col + 1) — B0) ^ 2
Next j
If num_y_col <> 1 Then
D_vosp = D_opyt / num_rows ‘дисперсия воспроизводимости опытов
Else
D_vosp = B0 * 0.05
End If
‘Расчет коэффициентов корреляции расширенной матрицы эффектов
‘с матрицей откликов
ReDim cor_mat_y(1 To Num_Ext_col)
For i = 1 To Num_Ext_col
cor_mat_y(i) = calc_cor(i, Num_Ext_col + 1, num_rows)
Next i
‘Определение списка регрессоров-кандидатов на предмет
‘их вхождения в структуру математической модели
newcand = 0
‘количество кандидатов не должно превышать кол. строк — 2
ReDim listcandw(num_rows)
ReDim kof_norm_mod(num_rows)
MP.max_share = 0.01
MP.cor_y = 0.01
ReDim Preserve xok(num_rows, Num_Ext_col + 2)
defcand
‘формирование массива имен главных эффектов
ReDim mef(1 To MEFF)
nef = Array(«x», «z», «u», «v», «w», «m», «n», «p»)
k1 = 0
For m = 1 To num_factor
For n1 = 1 To dp(m)
k1 = k1 + 1
mef(k1) = nef(n1) & m
Next n1
Next m
‘Вставка нового листа и вывод на него столбцов эффектов,
‘отобранных для включения в модель
Dim count_w
Worksheets.Add.Move after:=Worksheets(Worksheets.Count)
count_w = Worksheets.Count
Worksheets(count_w).Name = «Regression» & count_w
Worksheets(count_w).Cells(1, 1) = _
«Результаты программы отбора эффектов для регрессионного анализа»
‘Вывод матрицы эффектов, которые, были отобраны
‘на предмет включения в регрессионную модель
Worksheets(count_w).Cells(4, 1) = «Имена эффектов»
Worksheets(count_w).Cells(4, 1).Columns.AutoFit
Worksheets(count_w).Cells(3, 1) = «Коэф. коррел.»
Worksheets(count_w).Cells(2, 1) = «Коэф. норм.»
With Worksheets(count_w)
.Range(.Cells(3, 1), _
.Cells(3, 2 + newcand)).Borders.Item(xlTop).LineStyle = xlContinuous
.Range(.Cells(3, 1), _
.Cells(3, 2 + newcand)).Borders.Item(xlBottom).LineStyle = xlContinuous
End With
For cur_i = 1 To newcand
deint (listcandw(cur_i))
With Worksheets(count_w)
.Cells(4, 1 + cur_i).Value = texed
.Cells(4, 1 + cur_i).Font.Bold = True
.Cells(4, 1 + cur_i).Borders.Item(xlRight).LineStyle = xlContinuous
.Cells(4, 1 + cur_i).Borders.Item(xlBottom).LineStyle = xlDouble
.Cells(4, 1 + cur_i).HorizontalAlignment = xlCenter
End With
Worksheets(count_w).Cells(2, 1 + cur_i) = kof_norm_mod(cur_i)
Worksheets(count_w).Cells(3, 1 + cur_i) = cor_mat_y(listcandw(cur_i))
For i = 1 To num_rows
Worksheets(count_w).Cells(4 + i, 1 + cur_i) = xok(i, listcandw(cur_i))
Next i
With Worksheets(count_w)
.Range(.Cells(4, 1 + cur_i), _
.Cells(4 + num_rows, 1 + cur_i)).Borders.Item(xlRight).LineStyle = xlContinuous
End With
Next cur_i
With Worksheets(count_w).Cells(4, 2 + newcand)
.Value = «Y»
.Font.Bold = True
.HorizontalAlignment = xlCenter
.Borders.Item(xlBottom).LineStyle = xlDouble
End With
For i = 1 To num_rows
Worksheets(count_w).Cells(4 + i, 2 + newcand) = xok(i, Num_Ext_col + 1)
Next i
With Worksheets(count_w)
.Range(.Cells(4, 2 + newcand), _
.Cells(4 + num_rows, 2 + newcand)).Borders.Item(xlRight).LineStyle = xlDouble
End With
‘Вывод формул перевода
Worksheets(count_w).Cells(5 + num_rows, 1) = _
«Формулы перехода от натуральных значений к ортогональным контрастам»
Dim num_cur_row As Integer
num_cur_row = 1
For i = 1 To num_factor
For j = 1 To dpn(i)
For k2 = j + 1 To 1 Step -1
If k2 = j + 1 Then
If j = 1 Then texed = nef(j) & i & » = » & agn(i, j, k2) & » * (X» & i
If j <> 1 Then texed = nef(j) & i & » = » & agn(i, j, k2) & » * (x» & i & «^» & j
ElseIf k2 = 1 Then
If agn(i, j, k2) > 0 Then texed = texed & » + »
texed = texed & agn(i, j, k2) & «),»
Else
If agn(i, j, k2) = 0 Then GoTo e_loop
If agn(i, j, k2) > 0 Then texed = texed & » + »
texed = texed & agn(i, j, k2) & » * x» & i & «^» & k2 — j
End If
e_loop:
Next k2
Worksheets(count_w).Cells(5 + num_rows + num_cur_row, 1) = texed
num_cur_row = num_cur_row + 1
Next j
Next i
‘ Вывод условных обозначений
texed = «Условные обозначения исходных натуральных факторов»
Worksheets(count_w).Cells(7 + num_rows + MEFF, 1) = texed
For i = 1 To num_factor
texed = «X» & i & » — » & name_CELL.Cells(i)
Worksheets(count_w).Cells(8 + num_rows + MEFF + i, 1) = texed
Next i
e_sub:
End Sub
Function form_int2(kd As Integer) As Integer
Dim o1 As Integer, o5 As Integer, numchar As Integer
Dim CON_IN As String
o5 = mav(a2(1)) + a1(1) — 2
CON_IN = mef(o5)
kof_norm_mod(cur_i) = kof_norm(o5)
For o1 = 2 To kd
o5 = mav(a2(o1)) + a1(o1) — 2
CON_IN = CON_IN & mef(o5)
kof_norm_mod(cur_i) = kof_norm_mod(cur_i) * kof_norm(o5)
Next o1
texed = CON_IN
numchar = Len(texed)
lop = -1
form_int2 = numchar
End Function
Function cal_deg2(kd As Integer, N_H As Integer)
Dim op As Integer, id As Integer, cur As Integer, DEG As Integer
For id = 1 To kd
a1(id) = 1
Next id
While True
DEG = 0
For op = 1 To kd
DEG = DEG + a1(op)
Next op
If DEG <= deg_pol Or deg_pol = 0 Then
ly = ly + 1
If ly = N_H Then
form_int2 (kd)
End If
End If
a1(kd) = a1(kd) + 1
cur = kd
mh:
If a1(cur) > dpn(a2(cur)) Then
a1(cur) = 1
cur = cur — 1
If cur = 0 Then GoTo e_func
a1(cur) = a1(cur) + 1
GoTo mh
End If
Wend
e_func:
End Function
Function gen_san2(kd As Integer, N_H As Integer) As Integer
Dim ir As Integer, N As Integer, NM As Integer, p As Integer
N = 0: NM = 0
Dim tmp As Integer
For ir = 1 To kd
a2(ir) = ir
Next ir
p = kd
While True
tmp = cal_deg2(kd, N_H)
N = dpn(a2(1))
For ir = 2 To kd
N = N * dpn(a2(ir))
Next ir
NM = MN + N
If a2(kd) = num_factor Then p = p — 1
If a2(kd) < num_factor Then p = kd
If p >= 1 Then
For ir = kd To p Step -1
a2(ir) = a2(p) + ir — p + 1
Next ir
End If
If p < 1 Then GoTo e_func
Wend
e_func:
gen_san2 = NM
End Function
Function calc_int2(N_H As Integer)
Dim pw As Integer, ky As Integer
Dim tmp As Integer
ky = 1
ly = 0: lop = 0
For pw = 2 To num_factor
If ti(pw) = 1 Then
tmp = gen_san2(pw, N_H)
If lop = -1 Then Exit Function
End If
Next pw
If ti(num_factor) = 1 Then
For pw = 1 To num_factor
a2(pw) = pw
Next pw
tmp = cal_deg2(num_factor, N_H)
If lop = -1 Then Exit Function
End If
End Function
‘ deint — функция, предназначенная для формирования имени
‘ регрессора в строчной перемнной (строчке) texed (массив texed ї
‘ глобальным
‘ N_H — номер регрессора (столбца который отвечает регрессору)
‘ в росширенной матрице
Function deint(N_H As Integer) As Integer
Dim numchar As Integer
‘ 1. Проверка, существует ли такой номер ефекта в расширенной матрице */
If N_H < 1 Or N_H > Num_Ext_col Then deint = 0: Exit Function
‘ Если данный эффект есть главным (его имя сформировано и
‘ хранится в массиве mef */
If N_H <= MEFF Then
kof_norm_mod(cur_i) = kof_norm(N_H)
texed = mef(N_H)
GoTo plk
End If
‘/* 3. Этот регрессор по своему номеру принадлежит к взаимодействиям,
‘ которые генерируются автоматически */
If N_H > MEFF And N_H <= Num_Ext_col Then
N_H = N_H — MEFF
calc_int2 (N_H)
GoTo plk
End If
plk:
deint = numchar
End Function
Function defcand()
Dim Ycp As Double, Xcp As Double
Dim k1 As Integer
Dim Imax As Integer, i As Integer, j As Integer
Dim Rmax As Double, Ds As Double, Dpi As Double
Dim r As Double, B As Double
If MP.cor_y <= 0 Then s_error = 1: Exit Function
‘ Вычисление среднего значения отклика
Ycp = Y_aver
For j = 1 To num_rows
Y_mod(j) = xok(j, Num_Ext_col + 1)
xok(j, Num_Ext_col + 2) = xok(j, Num_Ext_col + 1)
Next j
‘ Определить Ds
Ds = d_sum
While True
Rmax = 0
Xcp = 0
For k1 = 1 To Num_Ext_col
‘ расчет среднего значения столбца матрицы ХОК
Xcp = 0
For j = 1 To num_rows
Xcp = Xcp + xok(j, k1)
Next j
Xcp = Xcp / num_rows
‘ Посчитать новое Ry
d = d1 = d2 = 0
r = Abs(calc_cor(k1, Num_Ext_col + 2, num_rows))
‘ Запомнить Rmax, Imax
If r > Rmax Then
Rmax = r
Imax = k1
End If
Next k1
If Rmax < MP.cor_y Then s_error = 5: Exit Function
For j = 1 To newcand
If Imax = listcandw(j) Then s_error = 6: Exit Function
Next j
‘ Посчитать коэффициент
Xcp = 0
For j = 1 To num_rows
Xcp = Xcp + xok(j, Imax)
Next j
Xcp = Xcp / num_rows
d = 0: d1 = 0:
For j = 1 To num_rows
d = d + (xok(j, Imax) — Xcp) * (xok(j, Num_Ext_col + 2) — Ycp)
d1 = d1 + (xok(j, Imax) — Xcp) ^ 2
Next j
B = d / d1
newcand = newcand + 1: listcandw(newcand) = Imax
If newcand = num_rows — 2 Then s_error = 7: Exit Function
‘ Снять влияние
For j = 1 To num_rows
xok(j, Num_Ext_col + 2) = xok(j, Num_Ext_col + 2) — B * xok(j, Imax)
Next j
‘ Проверить окончание
Ycp = 0
For j = 1 To num_rows
Ycp = Ycp + xok(j, Num_Ext_col + 1)
Next j
Ycp = Ycp / num_rows
Dpi = 0
For j = 1 To num_rows
Dpi = Dpi + (xok(j, Num_Ext_col + 2) — Ycp) ^ 2
Next j
If (Dpi / Ds) < MP.max_share Then s_error = 0: Exit Function
Wend
End Function
Function calc_cor(num_i As Integer, _
num_j As Integer, num_r As Integer) As Double
Dim u As Integer
Dim X1_midl As Double, X2_midl As Double
Dim X1_sub As Double, X2_sub As Double, X1_sum_squre As Double, X2_sum_squre As Double
Dim Sum_uper As Double, Sum_down As Double
s_error = 0
‘ Вычисление среднего по первому и второму столбику
X1_midl = 0
X2_midl = 0
For u = 1 To num_r
X1_midl = X1_midl + xok(u, num_i)
X2_midl = X2_midl + xok(u, num_j)
Next u
X1_midl = X1_midl / num_r
X2_midl = X2_midl / num_r
X1_sub = X2_sub = X1_sum_squre = X2_sum_squre = 0
Sum_uper = Sum_down = 0
For u = 1 To num_r
X1_sub = xok(u, num_i) — X1_midl
X2_sub = xok(u, num_j) — X2_midl
Sum_uper = Sum_uper + X1_sub * X2_sub
X1_sum_squre = X1_sum_squre + X1_sub * X1_sub
X2_sum_squre = X2_sum_squre + X2_sub * X2_sub
Next u
Sum_down = Sqr(X1_sum_squre * X2_sum_squre)
If Sum_down = 0 Then s_error = 1: calc_cor = 0: Exit Function
calc_cor = Sum_uper / Sum_down
End Function
‘ Анализ матрицы по столбцах на предмет определения
‘ степени факторов (количества уровней)
Function anal_X()
Dim val_X(1 To 10) As Double
Dim pe As Integer, kf As Integer, l As Integer
For kf = 1 To num_factor
For i = 1 To 10
val_X(i) = 0
Next i
val_X(1) = x_data_CELL.Cells(1, kf).Value
pe = 1
For j = 2 To num_rows
l = 0
For N = 1 To pe
If val_X(N) = x_data_CELL.Cells(j, kf).Value Then l = 1
Next N
If l = 0 Then
pe = pe + 1
val_X(pe) = x_data_CELL.Cells(j, kf).Value
End If
If pe = 10 Then GoTo end_sub
Next j
dpz(kf) = pe — 1
dp(kf) = pe — 1
If pe = 1 Then
s_error = -1
GoTo end_sub
End If
Next kf
For N = 1 To num_factor
If dpz(N) > 8 Then dpz(N) = 8
If dp(N) > 3 Then dp(N) = 3
Next N
vid.pfe = dpz(1) + 1
For kf = 1 To num_factor
vid.pfe = vid.pfe * dpz(kf) + 1
Next kf
If vid.pfe = num_rows Then
vid.pfe = 1
Else
vid.pfe = 0
End If
end_sub:
End Function
‘Подпрограмма расчета формул перехода от натуральных
‘значений к ортогональным контрастам
Function or_con_ft()
Dim mj, i, j As Integer
Dim but1, but2, max As Double
num_xok_col = 0
For var_c = 1 To num_factor
For mj = 1 To num_rows
X(mj) = x_data_CELL.Cells(mj, var_c).Value
Next mj
For i = 1 To 8
For j = 1 To 9
agn(var_c, i, j) = 0
Next j
Next i
For deg_c = 1 To dp(var_c)
If deg_c > 2 Then
For mj = 1 To num_rows
X(mj) = X1(mj)
Next mj
End If
For i = 1 To 10
bk(i) = 0
Next i
If deg_c < 3 Then sol_equal (deg_c)
If deg_c > 2 Then sol_equal1 (deg_c)
For i = 1 To deg_c
but1 = Abs(bk(i))
If (but1 < 0.000000001) Then bk(i) = 0
Next i
calcul
num_xok_col = num_xok_col + 1
For i = 1 To num_rows
xok(i, num_xok_col) = X(i)
Next i
Next deg_c
Next var_c
End Function
‘Формированиии информации о преобразовании данных
Function open_fil()
MEFF = 0 ‘Общая сумма степеней
For i = 1 To num_factor
MEFF = MEFF + dp(i)
Next i
max_deg = dp(1) ‘максимальная возможная степень фактора
For i = 2 To num_factor
If dp(i) > max_deg Then max_deg = dp(i)
Next i
End Function
‘Расчет формул перехода для степени меньше 3
Function sol_equal(DEG As Integer)
If DEG = 1 Then
For i = 1 To num_rows
bk(1) = bk(1) + X(i)
Next i
bk(1) = bk(1) / (-num_rows)
GoTo e_sub
End If
For i = 1 To num_rows
bk(1) = bk(1) + X(i) ^ 2
bk(2) = bk(2) + X(i) ^ 3
Next i
bk(2) = bk(2) / (-bk(1))
bk(1) = bk(1) / (-num_rows)
e_sub:
End Function
‘Расчет формул перехода для степени больше 2
Function sol_equal1(DEG As Integer)
Dim qo As Integer, f1 As Integer, f2 As Integer, f3 As Integer, j As Integer
Dim feo As Double
For qo = 1 To DEG + 1
For f1 = 1 To DEG
a(f1, qo) = 0
For f2 = 1 To num_rows
X(f2) = X1(f2)
Next f2
If f1 > 1 Then calcul1 (f1)
For f3 = 1 To num_rows
feo = X1(f3) ^ qo
If f1 = 1 Then a(f1, qo) = a(f1, qo) + feo
If f1 > 1 Then a(f1, qo) = a(f1, qo) + X(f3) * feo
Next f3
Next f1
Next qo
For qo = 1 To DEG
bk(qo) = -a(qo, DEG)
a(qo, DEG) = 0
Next qo
If a(DEG — 1, DEG — 1) <> 0 Then
bk(DEG — 1) = bk(DEG — 1) / a(DEG — 1, DEG — 1)
End If
For f1 = DEG — 2 To 1 Step -1
For f2 = f1 To DEG — 1
bk(f1) = bk(f1) — bk(f2 + 1) * a(f1, f2 + 1)
Next f2
bk(f1) = bk(f1) / a(f1, f1)
Next f1
For j = 1 To num_rows
X(j) = X1(j)
Next j
End Function
‘Расчет кодированных значений фактора по формулам
Function calcul()
Dim but1, but2, but3, max As Double
Dim mj, nj, r1, i As Integer
max = 0
For mj = 1 To num_rows
but2 = X(mj) ^ deg_c
but1 = bk(1) + but2
For nj = 2 To deg_c + 1
but2 = X(mj) ^ nj
but2 = but2 * bk(nj)
but1 = but1 + but2
Next nj
X(mj) = but1
but3 = Abs(X(mj))
If but3 > max Then max = but3
Next mj
If max <> 0 Then
For mj = 1 To num_rows
X(mj) = X(mj) / max
Next mj
bk(deg_c + 1) = 1 / max
End If
For i = 1 To deg_c + 1
agn(var_c, deg_c, i) = bk(i)
Next i
If deg_c = 1 Then
For mj = 1 To num_rows
X1(mj) = X(mj)
Next mj
End If
End Function
‘Расчет кодированных значений фактора по формулам
Function calcul1(pit As Integer)
Dim but1, but2, but3, max As Double
Dim mj, nj, r1 As Integer
max = 0
For mj = 1 To num_rows
but2 = X(mj) ^ pit
but1 = agn(var_c, pit, 1) + but2
For nj = 2 To pit
but2 = X(mj) ^ nj
but2 = but2 * agn(var_c, pit, nj)
but1 = but1 + but2
Next nj
X(mj) = but1
If max <> 0 Then X(mj) = X(mj) / agn(var_c, pit, pit)
Next mj
End Function
‘Вычисление нормировочных коэффициентов исходных данных
Function norm()
Dim summa As Double, koef1 As Double, koef2 As Double
Dim i As Integer, j As Integer
Dim D_N As Double
D_N = num_rows
For i = 1 To MEFF
summa = 0
For K = 1 To num_rows
X(K) = xok(K, i)
Next K
For j = 1 To num_rows
summa = summa + X(j) * X(j)
Next j
koef1 = summa / D_N
koef2 = Sqr(koef1)
If koef2 <> 0 Then
For j = 1 To num_rows
X(j) = X(j) / koef2
Next j
End If
For K = 1 To num_rows
xok(K, i) = X(K)
Next K
kof_norm(i) = koef2
Next i
End Function
‘Вычисление количества и степеней взаимодействий
Function calc_int()
Dim sum As Integer, Num_it As Integer, pw As Integer
Dim br As Integer, nr As Integer
Num_inef = 0
For br = 1 To MEFF
D_I(br) = 0
Next br
For br = 1 To num_factor
If deg_eff = 0 Then
dpn(br) = dp(br)
GoTo e_for
End If
dpn(br) = dp(br)
If deg_eff > 0 And dp(br) > deg_eff Then dpn(br) = deg_eff
e_for:
Next br
MD = 0
For pw = 2 To num_factor
If ti(pw) = 1 Then Num_inef = Num_inef + gen_san(pw)
Next pw
If ti(num_factor) = 1 Then
num_int = dpn(1)
For pw = 1 To num_factor
Num_it = Num_it * dpn(pw)
Next pw
Num_inef = Num_inef + Num_it
For pw = 1 To num_factor
a2(pw) = pw
Next pw
cal_deg (Num_ST)
End If
If deg_pol > 1 Then
Num_inef = 0
For br = 2 To deg_pol
Num_inef = Num_inef + D_I(br)
Next br
End If
End Function
Function gen_san(kd As Integer) As Integer
Dim ir As Integer, N As Integer, NM As Integer, p As Integer
For ir = 1 To kd
a2(ir) = ir
Next ir
p = kd
While p > 0
cal_deg (kd)
N = dpn(a2(1))
For ir = 2 To kd
N = N * dpn(a2(ir))
Next ir
NM = NM + N
If a2(kd) = num_factor Then p = p — 1
If a2(kd) < num_factor Then p = kd
If p >= 1 Then
For ir = kd To p Step -1
a2(ir) = a2(p) + ir — p + 1
Next ir
End If
If p < 1 Then GoTo e_f
Wend
e_f: gen_san = NM
End Function
Function cal_deg(kd As Integer)
Dim op As Integer, id As Integer, cur As Integer, DEG As Integer
For id = 1 To kd
a1(id) = 1
Next id
While True
DEG = 0
For op = 1 To kd
DEG = DEG + a1(op)
Next op
D_I(DEG) = D_I(DEG) + 1
If MD = 1 Then
If DEG <= deg_pol Or deg_pol = 0 Then gen_int (kd)
End If
a1(kd) = a1(kd) + 1
cur = kd
mh:
If a1(cur) > dpn(a2(cur)) Then
a1(cur) = 1
cur = cur — 1
If cur = 0 Then GoTo e_f
a1(cur) = a1(cur) + 1
GoTo mh
End If
Wend
e_f:
End Function
Function cret_int()
Dim pw As Integer, i As Integer, j As Integer
mav(1) = 0
mav(1) = dp(1)
For i = 2 To num_factor
mav(i) = 0
For j = 1 To i
mav(i) = mav(i) + dp(j)
Next j
Next i
MD = 1
For pw = 2 To num_factor
If ti(pw) = 1 Then gen_san (pw)
Next pw
If ti(num_factor) = 1 Then
For pw = 1 To num_factor
a2(pw) = pw
Next pw
cal_deg (num_factor)
End If
End Function
Function gen_int(kd As Integer)
Dim o1 As Integer, o2 As Integer, o3 As Integer, o5 As Integer
For o1 = 1 To kd
o5 = mav(a2(o1)) + a1(o1) — 2
‘обчислення номера стовбчика ефекта
For o2 = 1 To num_rows
X(o2) = xok(o2, o5)
Next o2
If o1 = 1 Then
For o2 = 1 To num_rows
X1(o2) = X(o2)
Next o2
GoTo e_loop
End If
For o2 = 1 To num_rows
X1(o2) = X1(o2) * X(o2)
Next o2
e_loop:
Next o1
‘ запис розрахованої взаємодії у файл розширеної мариці
‘ (його диписування до кінця матриці
writ_int
End Function
Function writ_int()
Dim i1 As Integer
Num_Ext_col = Num_Ext_col + 1
ReDim Preserve xok(num_rows, Num_Ext_col)
For i1 = 1 To num_rows
xok(i1, Num_Ext_col) = X1(i1)
Next i1
End Function
6.9. Пример
Всякое искусство зависит от упражнения
Вегеций,
«Краткое изложение основ военного дела»
Рассмотрим типичную задачу по определению оптимального состава лекарственного препарата. У нас есть три компонента А, Б и В. Необходимо подобрать оптимальное соотношение между ними. Оптимальная комбинация должна обеспечить наилучшие требуемые свойства, например, анальгезирующую или противовоспалительную активность.
При исследованиях, кроме компонент состава, обычно изменяются еще и дозы лекарственного средства. Кроме того, эффект от применения препарата замеряется несколько раз через определенные периоді. Это необходимо для оценки изменения эффекта во времени.
В полном объеме выполнение регрессионного анализа в Excel так, как описано выше невозможно. Добавленные программы позволяют эффективно решать средние по размеру и сложности задачи. Для решения больших и сложных задач следует использовать статистическое программное обеспечение, например, ПС ПРИАМ.
6.9.1. Формирование плана эксперимента
Определим необходимое количество опытов. Есть три фактора — компонента. Каждый из них достаточно изменять на трёх уровнях. Дозу будем менять на четырех уровнях. То есть нам нужен план вида 3341//? с неизвестным пока количеством опытов. Количество опытов определим по формуле (6.10).
N=(1,5..2)*(1+ 3*(3-1)+1*(4-1))=(1,5..2)*10=15..20.
Таким образом, количество экспериментов должно быть 15–20. В приложении З есть таблица на 18 опытов, которая (см. табл. 3.4) нам подходит. Необходимый нам план выбирается следующим образом. Нам нужно три фактора на трех уровнях и один — на четырех. Для этого воспользуемся табл. 3.5 и 3.6. По структуре и размерам они идентичны, но табл. 3.5 содержит количество уровней варьирования, а табл. 3.6 — номера соответствующих столбцов табл. 3.4. Столбец на четырех уровнях только один — под номером 9. Обратите внимание: столбцы, номера которых находятся в табл. 3.6 в одном вертикальном столбце, не должны входить в одну матрицу планирования. В нашем случае, поскольку мы выбрали 9-й столбец, столбцы 1, 2, 10, 11 не могут включаться в матрицу. Необходимые нам три фактора на трёх уровнях — столбцы 3, 4, 5. Для формирования окончательного нашего плана из табл. 3.4 следует взять столбцы 3, 4, 5, 9. В результате получаем матрицу плана эксперимента 3341//18, приведенную в табл. 6.8.
Таблица 6.8
Матрица эксперимента
| Номер опыта | Х1 | Х2 | Х3 | Х4 |
| 1 | 0 | 0 | 0 | 0 |
| 2 | 0 | 1 | 1 | 1 |
| 3 | 0 | 2 | 2 | 2 |
| 4 | 1 | 1 | 2 | 0 |
| 5 | 1 | 2 | 0 | 1 |
| 6 | 1 | 0 | 1 | 2 |
| 7 | 2 | 2 | 1 | 0 |
| 8 | 2 | 0 | 2 | 1 |
| 9 | 2 | 1 | 0 | 2 |
| 10 | 0 | 0 | 0 | 3 |
| 11 | 0 | 1 | 1 | 0 |
| 12 | 0 | 2 | 2 | 1 |
| 13 | 1 | 1 | 2 | 3 |
| 14 | 1 | 2 | 0 | 0 |
| 15 | 1 | 0 | 1 | 1 |
| 16 | 2 | 2 | 1 | 3 |
| 17 | 2 | 0 | 2 | 0 |
| 18 | 2 | 1 | 0 | 1 |
Здесь значения уровней варьирования условные, поэтому для проведения эксперимента их необходимо заменить натуральными значениями факторов. Для этого сначала сформируем таблицу соответствия кодированных и натуральных значений (табл. 6.9).
Таблица 6.9
Соответствие кодированных и натуральных значений факторов
| Кодированные значения | Натуральные значения уровней факторов | ||||
| уровней факторов | Компонент 1 | Компонент 2 | Компонент 3 | Доза | |
| 0 | 15 | 4 | 21 | 10 | |
| 1 | 20 | 8 | 28 | 20 | |
| 2 | 30 | 12 | 35 | 30 | |
| 3 | – | – | – | 40 | |
После этого формируем рабочую матрицу (табл. 6.10), заменяя кодированные значения соответствующими натуральными.
Таблица 6.10
Рабочая матрица
| Номер опыта | Компонент 1 | Компонент 2 | Компонент 3 | Доза |
| 1 | 15 | 4 | 21 | 10 |
| 2 | 15 | 8 | 28 | 20 |
| 3 | 15 | 12 | 35 | 30 |
| 4 | 20 | 8 | 35 | 10 |
| 5 | 20 | 12 | 21 | 20 |
| 6 | 20 | 4 | 28 | 30 |
| 7 | 30 | 12 | 28 | 10 |
| 8 | 30 | 4 | 35 | 20 |
| 9 | 30 | 8 | 21 | 30 |
| 10 | 15 | 4 | 21 | 40 |
| 11 | 15 | 8 | 28 | 10 |
| 12 | 15 | 12 | 35 | 20 |
| 13 | 20 | 8 | 35 | 40 |
| 14 | 20 | 12 | 21 | 10 |
| 15 | 20 | 4 | 28 | 20 |
| 16 | 30 | 12 | 28 | 40 |
| 17 | 30 | 4 | 35 | 10 |
| 18 | 30 | 8 | 21 | 20 |
Согласно построенной рабочей матрице выполняются эксперименты. При этом следует учитывать требования, изложенные в 6.4. Результаты эксперимента помещаются в табл. 6.11 (первые четыре столбца).
Таблица 6.11
Результаты эксперимента
| Номер опыта | Результаты повторных опытов | Среднее | Дисперсия | ||
| 1 | 2 | 3 | |||
| 1 | 98,5 | 97,2 | 99,5 | 98,4 | 1,323333 |
| 2 | 94,5 | 73,6 | 96,5 | 88,2 | 134,41 |
| 3 | 157,9 | 137,5 | 148,5 | 147,9667 | 38,47259 |
| 4 | 14,5 | 12,5 | 14,4 | 13,8 | 0,943333 |
| 5 | 108,5 | 88,5 | 99,5 | 98,83333 | 38,03704 |
| 6 | 297,5 | 308 | 306,5 | 304 | 4,083333 |
| 7 | 0,2 | 0,3 | 0,2 | 0,233333 | 0,002593 |
| 8 | 154,5 | 154,2 | 143,5 | 150,7333 | 29,80481 |
| 9 | 279,1 | 259,5 | 268,5 | 269,0333 | 28,69481 |
| 10 | 501,9 | 482,5 | 504,5 | 496,3 | 123,6133 |
| 11 | 32,5 | 34,3 | 35,5 | 34,1 | 0,573333 |
| 12 | 27,5 | 26,4 | 27,5 | 27,13333 | 0,313704 |
| 13 | 390,5 | 420,2 | 401,5 | 404,0667 | 102,7604 |
| 14 | 27,5 | 25,5 | 27,5 | 26,83333 | 1,037037 |
| 15 | 155,7 | 147,5 | 167,5 | 156,9 | 100,12 |
| 16 | 385,5 | 407,5 | 404,8 | 399,2667 | 17,61593 |
| 17 | 93,5 | 96,4 | 94,5 | 94,8 | 1,043333 |
| 18 | 151 | 159,5 | 152,5 | 154,3333 | 13,17593 |
6.9.2. Предварительный статистический анализ
Исходные данные и результаты предварительного статистического анализа приведены на рис. 6.19.
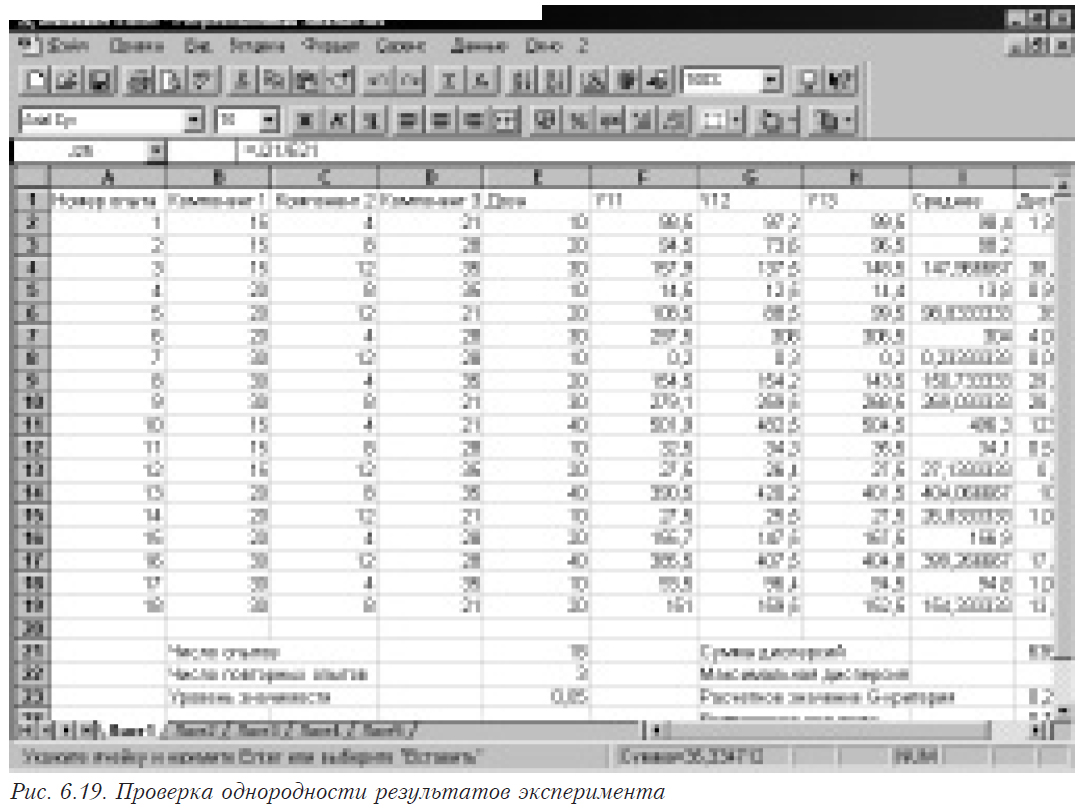
Рассчитываются средние значения по каждой строке эксперимента (=СРЗНАЧ(G2:I2) и размножаем на столбец) и дисперсии (=ДИСП(H2:J2) соответственно). Полученные столбцы средних и дисперсий помещаены в табл. 6.11.
После этого необходимо проверить однородность результатов эксперимента (подробности в 3.2.2).
Для этого рассчитываем сумму дисперсий (=СУММ(K2:K19)) и максимальную из дисперсий (=МАКС(K2:K19)), а затем расчетное значение критерия Кохрена (=K22/K21). Затем рассчитываем критическое значение критерия (=FРАСПОБР(E23/(E22-1);E21;(E22-2)*E21)/(FРАСПОБР(E23/(E22-1);E21;(E22-2)*E21)+E22-2)). Поскольку расчетное значение критерия меньше критического, то дисперсии однородны, и мы можем вычислить дисперсию воспроизводимости (=K21/E21).
6.9.3. Проверка однородности (неразрывности) факторного пространства
Для пассивного эксперимента необходимо обязательно провести анализ непрерывности факторного пространства, а затем выполнить работу с каждой из однородных подвыборок (см. 5.1). Поскольку в данном случае эксперимент активный, можно пропустить этот пункт и вернуться к нему только в том случае, если работа по построению модели закончится неудачей. Для анализа неразрывности к исходной матрице независимых переменных необходимо добавить столбец средних значений отклика.
6.9.4. Преобразования и отбор
Для того чтобы осуществить преобразование и отбор, выбираем в меню последовательно пункты «Сервис», «Макрос», «Макросы». В появившемся окне (его вид см. на рис. 5.6) выбираем «Build_Reg_Model». После этого последовательно появляется несколько окон, которые позволяют задать исходные данные для программы. Сначала необходимо задать ссылку на независимые переменные (рис. 6.20).
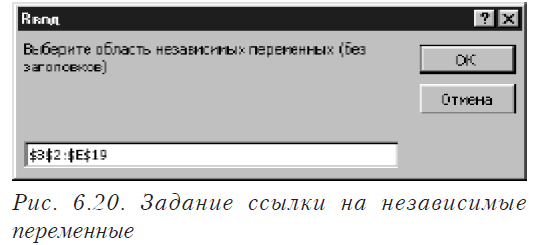
После этого необходимо ввести ссылку на зависимую переменную (рис. 6.21).
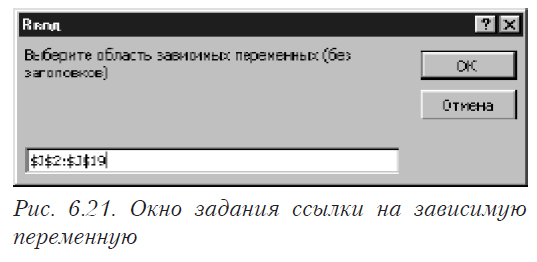
Обращаем ваше внимание, что вы здесь можете указать как ссылку на столбец средних, так и ссылку на несколько столбцов, которые представляют собой повторные опыты. В этом случае столбец средних будет рассчитан самой программой. После этого вы устанавливаете ссылку на имена независимых переменных (рис. 6.22).
Результатом работы программы будет матрица регрессоров, представляющих собой преобразованные исходные столбцы (см. 6.6.2). При этом в результирующей матрице будет оставлены только те регрессоры, которые потенциально могут войти в модель (см. 6.6.1). Для помещения результатов программа создает новый лист с именем RegressionN, где N – номер, на 1 больше номера последнего листа в рабочей книге. Результаты состоят из двух частей. Первая часть представляет собой данные, приготовленные для последующей обработки программой «Регрессия». Они состоят из матрицы преобразованных независимых переменных и столбца средних значений отклика. Здесь же помещаются коэффициенты нормировки столбцов (см. 6.6.2). Строка «Коэф. коррел.» содержит коэффициенты корреляции каждого регрессора с откликом. Эта информация представлена на рис. 6.23.
Для последующего включения в модель отобраны регрессоры Х4, Х2, Z4, X3, X2X3. Здесь Х4, Х2, X3 – линейные эффекты, Z4 – квадратичный (второй степени), а X2X3 – эффект взаимодействия переменных X2 и X3. На этой же странице программа представляет формулы преобразования к ортогональным контрастам (подробнее 6.6.2) и соответствие условных имен переменных натуральным (см. рис. 6.24).
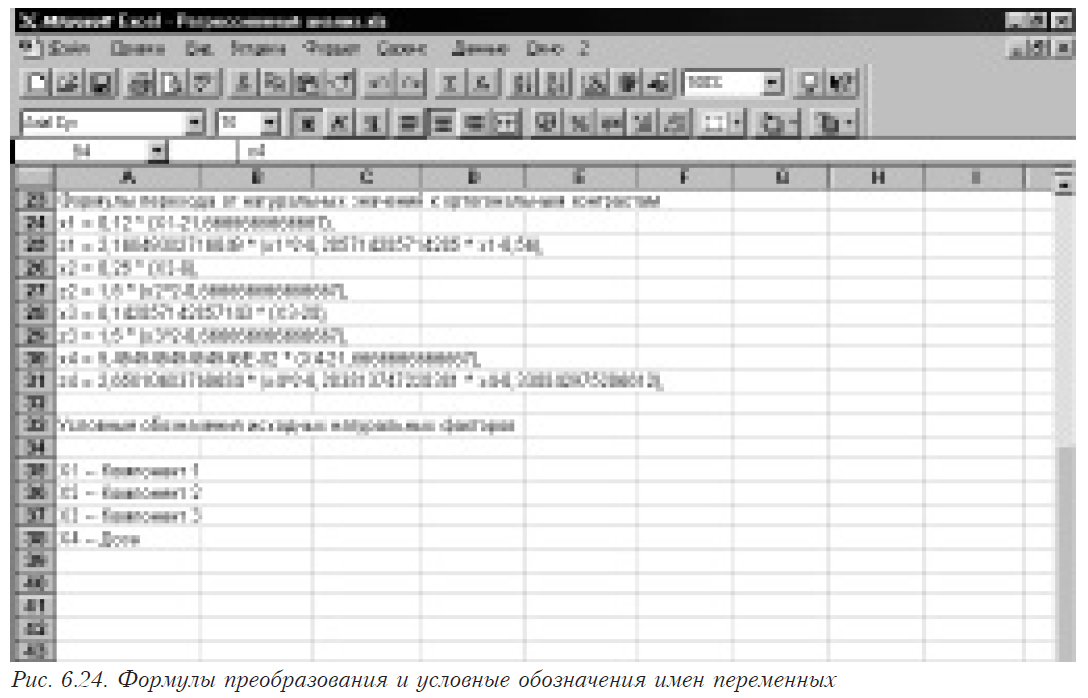
Формулы перехода в дальнейшем могут быть использованы в дальнейшем для расчетов по модели.
6.8.5. Получение коэффициентов
Выбираем последовательно пункты меню «Сервис», «Анализ данных». В появившемся окне (см. рис. 4.6) выбираем пункт «Регрессия». Появится окно (рис. 6.25).
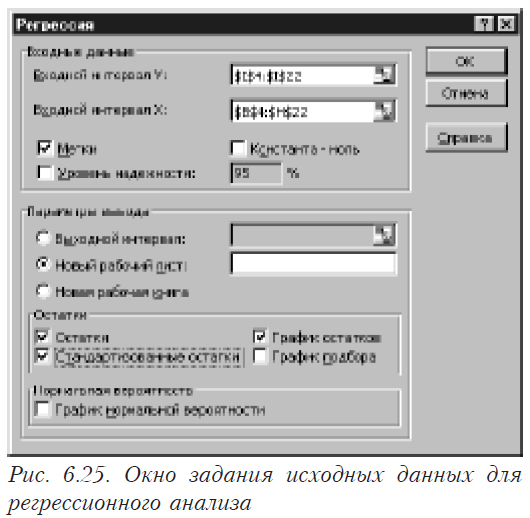
Входной интервал Y — вводится ссылка на столбец средних значений отклика.
Входной интервал Х — вводится ссылка на матрицу регрессоров, полученную в 6.8.4.
Уровень надежности — доверительная вероятность, которая используется при проверке всех статистических гипотез в регрессионном анализе.
Метки – выбираются в том случае, если вы, устанавливая ссылки на Х и У, включаете в ссылочную область и имена переменных.
Для вывода информации рекомендуем задавать Новый рабочий лист. Если вы хотите выводить и графики, то при некоторых способах подключения пакета анализа необходимо задать Новая рабочая книга.
Для дальнейшего анализа следует запросить (отметить) Остатки, Стандартизированные остатки и График остатков.
Результат работы программы приведен на рис. 6.26, 6.27, 6.28.
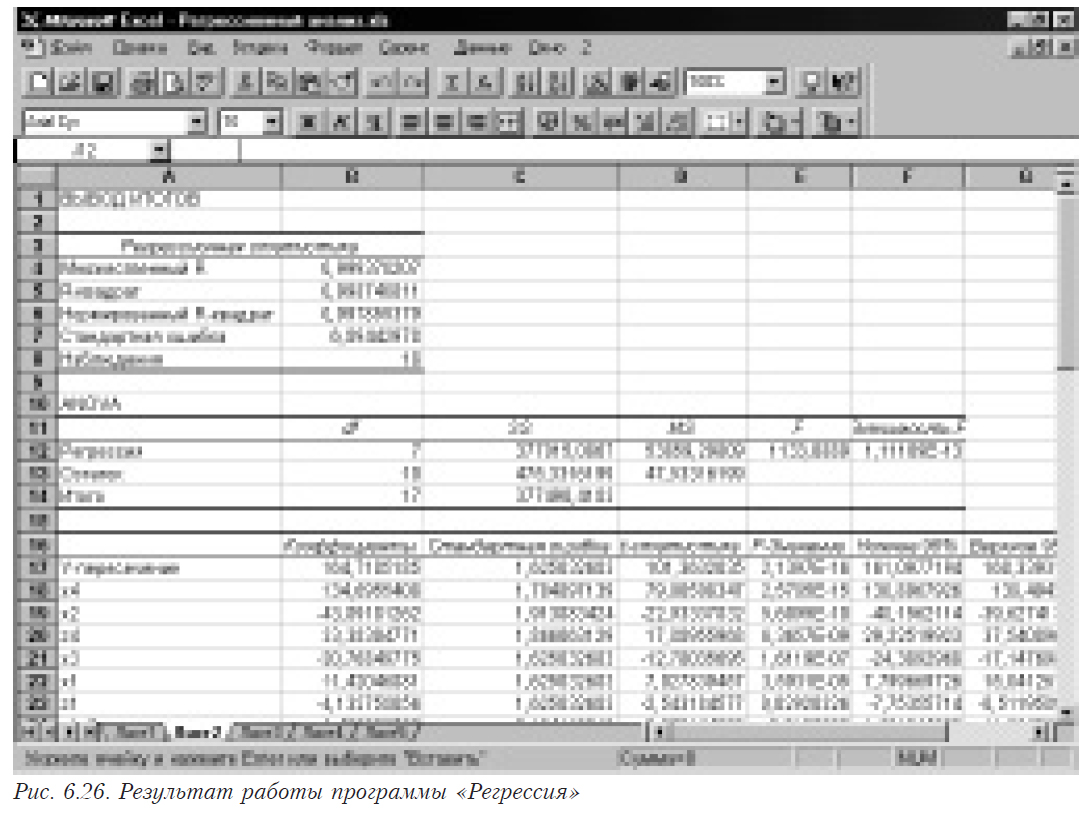
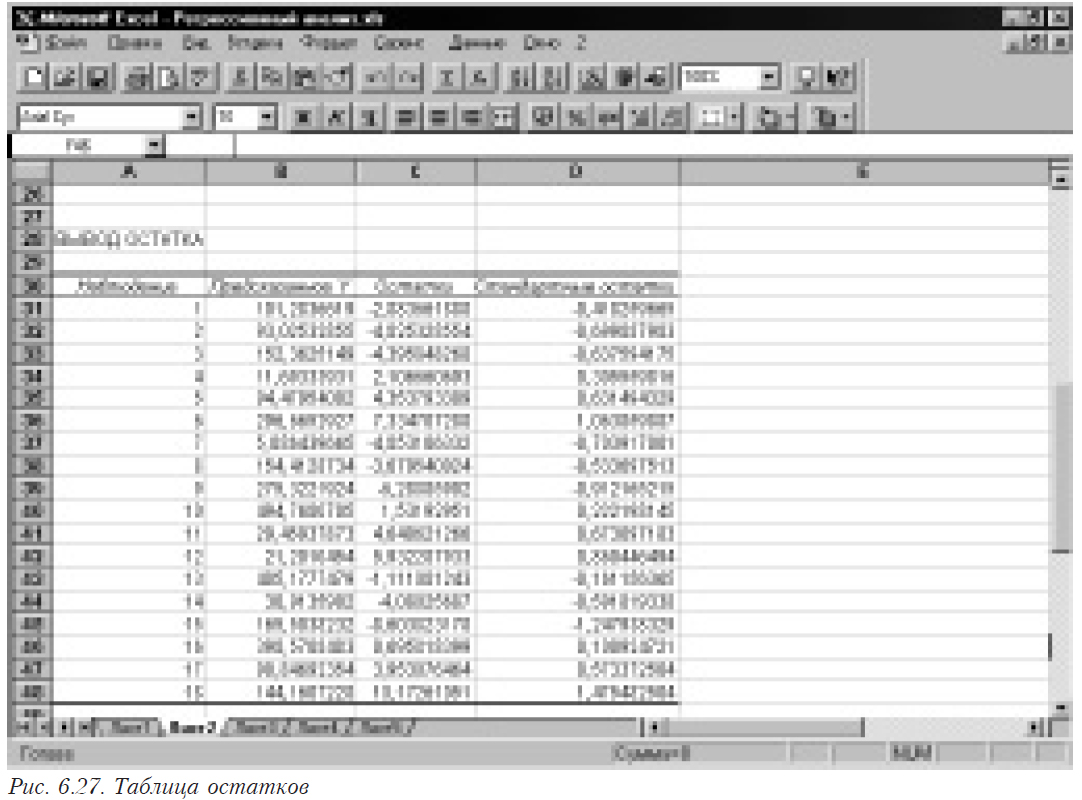

6.8.6. Анализ результатов построения модели
Программа выводит четыре таблицы: «Регрессионная статистика», «Дисперсионный анализ», «Вывод остатка», таблицу коэффициентов регрессии и их статистических характеристик.
Таблица остатков содержит столбец значений отклика, рассчитанных по модели (Предсказанное), и остатки. Графики остатков являются зависимостями графиков остатков от регрессоров. Как анализировать эту информацию см. 6.7.6.
Таблица коэффициентов регрессии и их статистических характеристик в первом столбце содержит названия коэффициентов, во втором — значение коэффициента регрессии, затем стандартное отклонение для него и расчетное значение t-статистики. Под Y-пересечением подразумевается свободный член. Регрессоры, для которых расчетное значение t-статистики меньше критического tµ,n (табличное значение критерия Стьюдента с уровнем значимости µ, и n степенями свободы; при этом n = N(n-1), где N — число экспериментов, а n — количество повторных опытов; вычисляется с помощью функции СТЬЮДРАСПОБР) должны быть удалены из модели. Для этого необходимо из таблицы, полученной в 6.8.5, удалить соответствующие столбцы, а затем повторить действия, начиная с 6.8.6. Для данной задачи критическое значение критерие Стьюдента вычисляется вызовом функции =СТЬЮДРАСПОБР(0,05;18*(2-1)). Оно равно 2,100924. Поскольку все расчетные значения больше него, то все коэффициенты регрессии значимы и удалять какой либо из модели нет необходимости.
Для оценки информативности модели (см. 6.7.1) используется таблица «Регрессионная статистика», а в ней — «Множественный R» (коэффициент множественной корреляции) и «R квадрат». Для определения значимости коэффициента множественной корреляции необходима дисперсия, объясняемая моделью (находится в табл. «Дисперсионный анализ» в ячейке на пересечении строки Регрессия и столбца MS), и остаточная дисперсия, которая находится в той же таблице в ячейке на пересечении строки Остаток и столбца MS. Расчетное значение критерия Фишера для оценки значимости множественного коэффициента регрессии находится в строке «Регрессия» и столбце «F» (565,602). Критическое значение вычисляется вызовом функции =FРАСПОБР(0,05;18-6;6-1), где 18 – число опытов, а 6 число членов модели. Оно равно 4,677702. Поскольку это значение меньше расчетного, то коэффициент регрессии значим. Более того, поскольку расчетное более чем в 100 раз больше критического, то параметр g критерия Бокса-Веца значительно больше 3.
Для анализа адекватности (см. 6.7.2) необходима остаточная дисперсия (см. ранее) и дисперсия воспроизводимости, полученная в 6.8.2 =[regr_ex.xls][18]Лист1!$K$25. Расчетное значение критерия Фишера для адекватности получается отношением дисперсия воспроизводимости к остаточной дисперсии. Поскольку это значение (0,265837) меньше 1, то необходимо проверка двухсторонней гипотезы. Верхнее критическое рассчитывается вызовом функции =FРАСПОБР(0,025;18*(3-1);18-1), а нижнее =FРАСПОБР(0,975;18*(3-1);18-1). Здесь 18 – число экспериментов, а 3 – кратность дублирования опытов. Так как расчетное значение находится вне предела (0,460656;2,462407), то модель неадекватна. В этой ситуации мы можем или пытаться добавить новые регрессоры в модель или же, если точность описания моделью экспериментальных данных нас устраивает, остановится на этой модели. Обращаем ваше внимание, что ситуации, когда модель высокоинформативна (коэффициент множественной корреляции близок к 1, а параметр g критерия Бокса-Веца большой) и модель неадекватна, обыно получаются при искуственно заниженной дисперсии воспроизводимости.
Для анализа устойчивости структуры модели необходимо построить корреляционную матрицу (см. 4.2.1) для матрицы, построенной в 6.8.5, а затем проанализировать ее (см. 6.7.3). Для этого выбираем последовательно пункты меню «Сервис», «Анализ данных», «Корреляция». В появившемся окне (рис. 6.29) необходимо задать исходные данные (они представлены на рис. 6.23)
Результатом работы будет корреляционная матрица, представленная на рис. 6.30. Из нее видно, что структура модели устойчива, т.к. коэффициенты корреляции каждого регрессора с откликом значительно превышают коэффициенты корреляции с любым другим регрессором (подробнее см. 6.7.3). Ниже приводится построенная таблица мультиколлинеарности (табл.6.12).

6.8.7. Счет по модели
При расчетах по модели необходимо учитывать двухступенчатые формулы пересчета. Т.е. сначала необходимо подставить исходные значения переменных в формулы перехода, а затем полученные значения в модель.Для получения расчетных формул перехода необходимо взять выведенные формулы перехода, начиная от «=» и ввести их в новую ячейку. Например, для получения х2 (см. рис.6.24) берем фрагмент =0,25*(Х2-8). Вместо Х2 необходимо подставить ссылку на значение «Компоненты 2», для которого необходимо выполнить рассчет по модели. Аналогично выполняются расчеты для остальных регрессоров. Затем полученные значения подставляются в модель. Для нашей задачи модель имеет вид =В17+ В18*х4+В19*х2+В20*z4+В21*х3+В22*х2*х3 (для понимания, откуда взяты коэффициенты см. рис. 6.26). Вместо х4, х2, z4, х3 необходимо подставить ссылки на вычисленные ранее значения этих регрессоров. Формулы для рассчетов для данного примера сведены в табл. 6.12, а результаты расчетов см. на рис. 6.31.
Таблица 6.12 Формулы для рассчета по модели.
| Название величины | Расчетная формула |
| x4 | = 0,25 * (C60-8) |
| x2 | = 0,142857142857143 * (D60-28) |
| z4 | = 0,0545454545454546 * (E60-21,6666666666667) |
| x3 | = 2,65010683760684 * (E63*E63-0,283813747228381 * E63-0,338842975206612) |
| Y | =B17+B18*E63+B19*C63+B20*F63+B21*D63+B22*C63*D63 |
6.8.8. Учет времени в качестве фактора
Иногда необходимо, чтобы в модели отражалась зависимость от времени. Допустим, что значение отклика замерялось через 1, 3 и 7 часов после введения препарата. Для того, чтобы ввести время четвертым фактором, необходимо размножить табл. 6.10 и ввести в нее столбец времени замера (табл. 6.13).
Таблица 6.13
Вид рабочей матрицы при введении фактора времени
| Номер | Факторы | Отклик | ||||
| опыта | Х1 | Х2 | Х3 | Х4 | Время | |
| 1 | 15 | 4 | 21 | 10 | 1 | У |
| 2 | 15 | 8 | 28 | 20 | 1 | |
| … | … | … | … | … | … | |
| 16 | 30 | 12 | 28 | 40 | 1 | При |
| 17 | 30 | 4 | 35 | 10 | 1 | Т=1 |
| 18 | 30 | 8 | 21 | 20 | 1 | |
| 19 | 15 | 4 | 21 | 10 | 3 | У |
| 20 | 15 | 8 | 28 | 20 | 3 | |
| … | … | … | … | … | … | |
| 34 | 30 | 12 | 28 | 40 | 3 | При |
| 35 | 30 | 4 | 35 | 10 | 3 | Т=3 |
| 36 | 30 | 8 | 21 | 20 | 3 | |
| 37 | 15 | 4 | 21 | 10 | 7 | У |
| 38 | 15 | 8 | 28 | 20 | 7 | |
| … | … | … | … | … | … | |
| 52 | 30 | 12 | 28 | 40 | 7 | При |
| 53 | 30 | 4 | 35 | 10 | 7 | Т=7 |
| 54 | 30 | 8 | 21 | 20 | 7 | |
Для полученной матрицы выполняется обработка как описано выше (начиная с 6.8.2). Желательно проверить с помощью кластерного анализа, можно ли считать полученную таким образом матрицу однородной. Это связано с тем, что очень часто структуры модели с различными временными показателями, существенно различаются.
Литература, рекомендуемая для изучения
- Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий.— 2-е изд., перераб. и доп.— М.: Наука, 1976.— 280с.
- Айвазян С.А., Енюков И.С., Мешалкин Л.Д. Прикладная статистика: Исследование зависимостей. — М.: Финансы и статистика, 1985. — 487с.
- Алгоритмы и программы восстановления зависимостей / Под ред. В.Н. Вапника. — М.: Наука, 1984.— 816с.
- Браунли К.А. Статистическая теория и методология в науке и технике.— М.: Наука, 1977. — 407с.
- Бродский В.З. Многофакторные регулярные планы.— М.: Изд-во МГУ, 1972.— 218с.
- Вучков И., Бояджиева Л., Солаков Е. Прикладной линейный регрессионный анализ.— М.: Финансы и статистика, 1987.— 239с.
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2 кн. — Кн. 1 / Пер. с англ.— М.: Финансы и статистика, 1986.— 386с.
- Дрейпер Н., Смит Г. Прикладной регрессионный анализ: В 2 кн. — Кн. 2 / Пер. с англ.— М: Финансы и статистика, 1987.— 351с.
- А Дубров.М., Мхитарян В.С., Трошин Л.И. Многомерные статистические методы. — М.: Финансы и статистика, 1998. — 352с.
- Енюков И.С. Методы, алгоритмы, программы многомерного статистического анализа.— М.: Финансы и статистика, 1986.— 232с.
- Загоруйко Н.Г., Орлов А.И. Некоторые нерешенные математические задачи прикладной статистики // Современные проблемы кибернетики. (Прикладная статистика).— М.: Знание, 1981.— 64с.
- Закс Л. Статистическое оценивание.— М.: Статистика, 1976.— 598с.
- Ивахненко А.Г., Мюллер Й.А. Самоорганизация прогнозирующих моделей.— К.: Техніка, 1984; Берлин: ФЕБ Ферлаб Техник, 1984.— 223с.
- Лапач С.Н. , Чубенко А.В. Применение современных количественных методов анализа в фармакологии и фармации // Фармакологічний вісник.— 1999.— № 1.— Додаток № 1.— 140с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка. — К.: ЗАО «Укрспецмонтажпроект», 1999. — 312с.
- Математическое обеспечение ЕС ЭВМ. — Вып. 14. — Минск: Ин-т математики АН БССР, 1978. — 320с.
- Н.С. Мисюк, А.С. Мастыркин, Г.П. Кузнецов Корреляционно-регрессионный анализ в клинической медицине. — М.: Медицина, 1975. — 192с.
- Мостеллер Ф., Тьюки Дж. Анализ данных и регрессия: В 2 вып.— Вып. 2: Пер. с англ. Б.Л. Розовского / Под ред. и с предисл. Ю.П. Адлера.— М.: Финансы и статистика, 1982.— 239с.
- Мэйдональд Дж. Вычислительные алгоритмы в прикладной статистике. — М.: Финансы и статистика, 1988.— 350с.
- Петрович М.Л. Регрессионный анализ и его математическое обеспечение на ЕС ЭВМ.— М.: Финансы и статистика, 1982. — 199с.
- Поллард Дж. Справочник по вычислительным методам статистики.— М.: Финансы и статистика, 1982. — 344с.
- Радченко С.Г. Математическое моделирование технологических процессов в машиностроении. — К.: ЗАО «Укрспецмонтажпроект», 1998. — 274 с.
- Райс Дж. Матричные вычисления и математическое обеспечение: Пер. с англ. О.Б. Арушаняна / Под ред. В.В. Воеводина. — М.: Мир, 1984. — 264с.
- Себер Д. Линейный регрессионный анализ: Пер. с англ. В.П. Носко / под ред. М.Б. Малютова. — М.: Мир, 1980. — 456с.
- Справочник по прикладной статистике: В 2 т. — Т. 1: Пер. с англ. / Под ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина. — М.: Финансы и статистика, 1989. — 510с.
- Справочник по прикладной статистике: В 2 т. — Т. 2: Пер. с англ.— М.: Финансы и статистика, 1990. — 526с.
- Таблицы планов эксперимента для факторных и полиноминальных моделей / Под ред. В.В. Налимова.— М.: Металлургия, 1982.— 752с.
- Трофимов В.П. Логическая структура статистических моделей.— М.: Финансы и статистика, 1985.— 191с.
- Устойчивые статистические методы оценки данных: Пер. с англ. — М.: Машиностроение, 1984. — 232с.
- Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа. Руководство для экономистов / Пер. с нем. и предисл. В.М. Ивановой.— М.: Финансы и статистика, 1983.— 304с.
- Форсайт Дж., Малькольм М., Моулер К. Машинные методы математических вычислений: Пер. с англ. Х.Д. Икрамова. — М.: Мир, 1980. — 280с.
- Хеттманспертер Т. Статистические выводы, основанные на рангах. — М.: Финансы и статистика, 1987. — 334с.
- Холлендер М., Вулф Д.А. Непараметрические методы статистики. — М.: Финансы и статистика, 1983. — 518 с.
- Хьюбер Дж. П. Робастность в статистике: Пер. с англ. — М.: Мир, 1984. — 304 с.
- Швырков В.В. Тайна традиционной статистики Запада. — М.: Финансы и статистика, 1998. — 144с.
[1] Лапач С.Н., Радченко С.Г., Бабич П.Н. Планирование, регрессия и анализ моделей PRIAM (ПРИАМ). SCMC‑90; 325, 660, 668 // Каталог. Программные продукты Украины. Catalog. Sofware of Ukraine.— К.: СП «Текнор», 1993.— С. 24–27.
[2] Satterthwaite F.E. Random Balance Experimentation. // Technometrics, 1959, v.1, № 2.
[3] Шуп Т. Решение инженерных задач на ЭВМ / Практическое руководство.— М.: Мир, 1982.— 238 с.
[4] Пример составлен Радченко С.Г.
[5] Лапач С.Н., Радченко С.Г., Бабич П.Н. Планирование, регрессия и анализ моделей PRIAM (ПРИАМ). SCMC=90; 325, 660, 668 // Каталог. Программные продукты Украины. Catalog. Sofware of Ukraine. — К.: СП «Текнор», 1993. — С. 24–27
[6] Вид небольшого оленя.
[7] Радченко С.Г. Математическое моделирования технологических процессов в машиностроении.— К.: ЗАО «Укрспецмонтажпроект», 1998.— 274 с.
[8] В специальной литературе можно встретить рекомендации о логарифмировании отклика в таких ситуациях. Действительно, в этом случае, дисперсии, как правило, становятся однородными. Но все полученные оценки будут относится к логарифмированному отклику, тогда как для исходного ничего не изменится.
[9] Барский В.Д., Забенко Л.А., Аксенина А.А., Беднов В.М. К вопросу о построении матрицы планирования отсеивающего эксперимента. // Заводская лаборатория. — 1971.— № 7, Т. 37, С. 721–825;
Мешалкин Л.Д. К обоснованию метода случайного баланса // Заводская лаборатория. — 1970.— № 3, Т. 36, С. 316–318;
Лапина З.С., Слободчикова Р.И. Исследование границ применимости алгоритма случайного баланса // Заводская лаборатория. — 1971, Т. 37, № 7.— С. 818–821;
Слободчикова Р.И., Фрейдлина В.Л., Лапина З.С., Налимов В.В. Повышение эффективности метода случайного баланса путем применения ветвящейся стратегии и электронно-вычислительных машин // Заводская лаборатория.— 1966.— № 1, Т. 32. — C. 53–58.
[10] Демиденко Е.З. Линейная и нелинейная регрессии.— М.: Финансы и статистика, 1981.— 302 с.
[11] Тихонов А.Н. Об обратных задачах // Некорректные задачи математической физики и анализа.— Новосибирск: Наука, 1984.— 264 с.
[12] Лучше совсем ничего не знать, чем знать плохо (лат.).
[13] Впервые встречается в 6.5.1.
[14] Иванов Г.А.,Турбан А.Ф. Статистические методы восстановления истинной зависимости по экспериментальным данным.— К.: Знание, 1986.— 22 с.
[15] Или как отношение максимального собственного числа к минимальному для матрицы левой части нормальных уравнений.
[16] Не забудьте, что число степеней свободы должно соответствовать контрольной выборке.
[17] Следует иметь в виду, что предсказания по модели с указанными ограничениями является интерполяцией, а не экстраполяцией.
[18] Ссылка на книгу, в которой находятся исходные данные и проведен предварительный статистический анализ