Статистика – универсальная методологическая наука, которая в состоянии измерить причинно-следственные зависимости.
В.В. Швырков «Тайна традиционной статистики Запада»
В статистическом анализе обычно различают следующие виды связей между факторами:
- функциональные;
- стохастические;
- статистические.
Функциональная связь — связь между переменными, при которой каждому значению одной величины соответствует строго определенное значение другой, то есть Y = F(X1, X2, …, Xn). Исследованием таких связей статистика не занимается.
Стохастическая связь — соответствует ситуации, когда изменение значения одной переменной ведет к изменению закона распределения другой. Для дискретного случая это означает, что каждому значению одной переменной соответствует набор значений другой, причем каждое значение имеет свою вероятность реализации. В данной книге не описаны методы, которые используются для изучения этих связей. В практических исследованиях наиболее известным видом таких связей являются марковские цепи.
Статистическая связь означает, что значение одной переменной изменяется в среднем в зависимости от того, какие значения принимает другая. Очень часто рассматривается как функциональная зависимость со случайной ошибкой, то есть
![]()
Где F(X1, X2,…, Xn) — функция, описывающая зависимость Y от совокупности независимых переменных X1,X2, …, Xn, а e — некоторая случайная ошибка. Известно, что сумма константы и случайной величины является случайной величиной. В связи с этим значения Y, рассчитанные по указанной формуле, будут вследствие добавления случайной величины e также случайными величинами.
В данном разделе рассматриваются методы, предназначенные для анализа (но не описания) статистических связей.
4.1. Выбор метода проверки наличия связи
Эти методы предназначены для проверки гипотез о наличии связей между переменными. Выбор метода зависит от шкал измерения, в которых измеряются анализируемые переменные, и от их количества (см. табл. 4.1).
Таблица 4.1
Выбор метода анализа связи между признаками
| Общее |
Шкалы измерения |
Закон распределения | Метод | |
| количество
переменных |
Влияющих переменных | Зависимой переменной | ||
| Две | интервалов или отношений |
Нормальный |
Параметрическая корреляция Пирсона | |
| Две | интервалов или отношений | Отличный от нормального | Непараметрическая корреляция Спирмена | |
| Две | Хотя бы одна порядка
|
— | Непараметрическая корреляция Спирмена или Кендалла | |
| Три и более | Порядка
|
— | Конкордация | |
| Две и более | наименований | интервалов или отношений |
Нормальный для зависимой переменной |
Параметрический дисперсионный анализ (критерий Фишера) |
| Две и более | наименований | интервалов или отношений | Порядка для зависимой переменной | Непараметрический дисперсионный анализ Зигеля и Тьюки |
| Две и более | наименований | интервалов или отношений | Отличный от нормального для зависимой переменной | Непараметрический дисперсионный анализ Зигеля и Тьюки |
| Три и более | наименований | порядка | — | Многомерный непараметрический дисперсионный анализ Фридмана |
| Три и более | наименований | интервалов или отношений | Отличный от нормального для зависимой переменной | Многомерный непараметрический дисперсионный анализ Фридмана |
| Три и более | наименований | интервалов или отношений | Нормальный для зависимой переменной | Многомерный параметрический дисперсионный анализ |
| Две | Обе наименования, причем одна вида «есть/нет», другая имеет только два значения | — | Четырехклеточные таблицы сопряженности | |
| Две | Обе наименования, одна вида «есть/нет», другая имеет К значений | — | Таблицы сопряженности вида 2хК | |
| Две | Обе наименования, одна имеет К значений уровней, другая — L | — | Таблицы сопряженности вида КхL | |
Из таблицы видно, что корреляционный анализ (параметрический или непараметрический) применяется в тех случаях, когда переменные измеряются в шкалах отношений, интервалов или порядка.
Дисперсионный анализ используют, если зависимая переменная измеряется в шкале отношений, интервалов или порядка, а влияющие переменные имеют нечисловую природу (шкала наименований).
Анализ таблиц сопряженности используется, когда влияющие переменные имеют нечисловую природу (шкала наименований), а зависимая переменная показывает количество наблюдений (% или долю от общего количества), для которых признак присутствует или отсутствует.
4.2. Корреляционный анализ
Знания следствия зависит от знания причины
Спиноза
Корреляционная связь представляет собой частный случай статистической связи , то есть математическое ожидание переменной Y, при условии, что случайная величина Х принимает значение х.
4.2.1. Параметрическая корреляция
(коэффициент корреляции Пирсона)
Предпосылка
- Все наблюдения взаимно независимые.
- Наблюдения имеют нормальный закон распределения.
Описание метода
Значение коэффициента корреляции вычисляется по формуле:

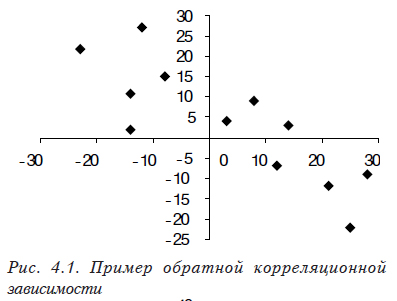
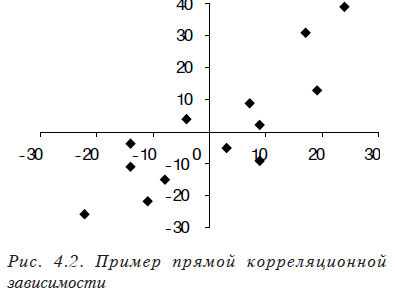
Коэффициент корреляции показывает тесноту линейной связи между двумя выборками случайных величин. Его значение изменяется от –1 (рис. 4.1, ), что соответствует обратной связи, до +1 (рис. 4.2, ), соответствующее прямо пропорциональной связи (значение 0, означает отсутствие связи (рис. 4.3).
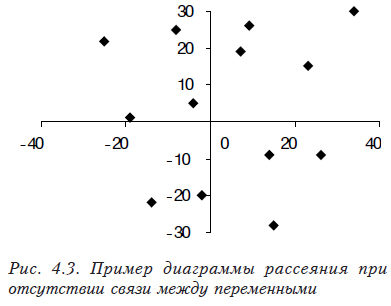
Значимость коэффициента корреляции. Поскольку мы имеем дело со случайными величинами, одной величины коэффициента парной корреляции для вывода недостаточно. Необходимо проверить, значимо ли он отличается от нуля. Это можно сделать с помощью критерия Стьюдента. Фактически проверяется гипотеза о равенстве коэффициента корреляции нулю. Для этого рассчитывается критериальное значение по формуле
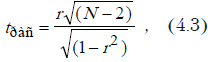
где r — значение коэффициента корреляции, а N — количество наблюдений.
Если расчетное значение t () больше табличного, взятого с N–2 степенями свободы, нулевая гипотеза отвергается. Это означает, что коэффициент корреляции значимо отличается от нуля (с выбранным уровнем значимости). Полуширина доверительного интервала для коэффициента корреляции определяется по формуле

где N — число наблюдений, по которым рассчитывается коэффициент корреляции; r — значение коэффициента корреляции; .— табличное значение критерия Стьюдента, взятого с N-2 степени свободы.
Примечание:
- При использовании корреляционного анализа следует помнить, что коэффициент корреляции показывает тесноту только линейной связи. Поэтому, в том случае, когда зависимости более сложные, чем линейные, коэффициент корреляции будет показывать отсутствие связи. Например, на рис. 4.4 хорошо видно, что между переменными существует зависимость второго порядка. Рассчитанный коэффициент корреляции будет близок к нулю, и проверка покажет, что он статистически незначим. Поэтому для определения сложных зависимостей между переменными используются другие статистические методы, наиболее часто и эффективно — регрессионный анализ, который будет рассмотрен в следующих разделах.
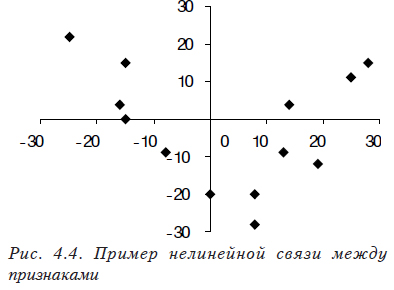
- Следует также помнить, что при наличии физической связи между переменными следствием обычно является наличие и корреляционной связи. Однако, если выборка нерепрезентативная, то есть содержит не те реализации случайной величины, которые позволяют определить зависимость, коэффициент корреляции будет близок к нулю и незначим. Например, рис.5 повторяет рис. 4.1, на котором присутствует обратная связь с коэффициентом корреляции близким к –1. В том случае, если выборка будет включать выделенные (круглые) точки, являющиеся подмножеством нашей выборки, то коэффициент парной корреляции будет близок к нулю.
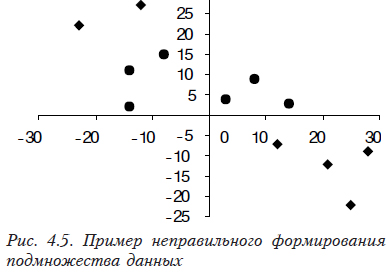
- С другой стороны, наличие статистической связи необязательно означает наличие физической. Причиной может быть нерепрезентативность выборки, как в предыдущем случае, или же тот факт, что исследуемая переменная Х не зависит от переменной Y, но обе они зависят от переменной Z. В этом случае при проведении корреляционного анализа мы видим связь между Х и Y, которая в физическом смысле отсутствует. Рассмотрим известный пример такой ситуации[1]. В Стокгольме в 60-е годы подсчитали коэффициент корреляции между количеством прилетающих аистов и количеством рождающихся детей. Он оказался близок к единице и статистически значим. Дело в том, что количество аистов зависело от количества отдельных домохозяйств, а количество детей и домохозяйств — от количества семей. И еще пример: в одном из штатов США установили наличие положительной корреляционной связи между количеством церквей и количеством баров — чем больше церквей, тем больше баров [5]. На самом деле обе эти величины зависели от размера города. Следует помнить о возможности существования аистов, приносящих младенцев, так как в большинстве случаев, возникающих при решении практических задач, абсурдность наличия или отсутствия физической связи неочевидна.
- Из наличия корреляционной связи, которая служит отражением действительно существующей физической связи, следует делать правильные выводы. Ведь из наличия обратной корреляционной связи между температурой воздуха на улице и количеством топлива, расходуемым на обогрев помещения, вовсе не следует вывод: «чем больше топишь печь , тем холоднее становится на улице».
Пример[2]
Взаимосвязь между объемом циркулирующей крови (ОЦК), объемом циркулирующей плазмы (ОЦП) и гематокритом (Ht) выражается формулой
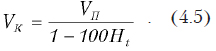
Получены экспериментальные данные — 21 наблюдение для этих величин. Нам необходимо определить степень зависимости между ними, используя коэффициент корреляции. Набрав исходные (столбцы А,В,С рис. 4.8) в меню выбираем Сервис, а затем Анализ данных. Появится окно выбора метода обработки (рис. 4.6).
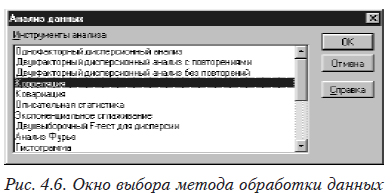
В этом окне выбираем Корреляция — появится окно задания исходных данных для корреляции (рис. 4.7).
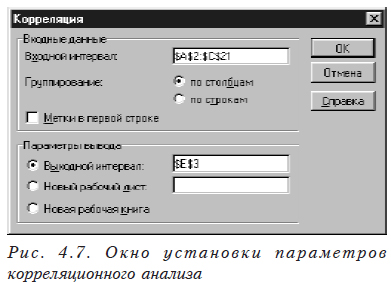
В нем необходимо задать исходные данные для корреляционного анализа.
Входной интервал — необходимо отметить таблицу, в которой размещены исходные данные (левая верхняя ячейка и правая нижняя).
Группирование — необходимо указать, в строках или столбцах находятся данные, относящиеся к одному уровню фактора (в данной ситуации по столбцам).
Выходной интервал — вводится ссылка на ячейку, расположенную в левом верхнем углу выходного диапазона (мета, куда вы хотите поместить результат). Размеры выходной области будут рассчитаны автоматически.
Новый рабочий лист — выбирается в случае, если вы хотите поместить результаты работы на другой лист; при этом в соответствующем окошке указывается диапазон размещения результатов аналогично предыдущему пункту.
Новая рабочая книга — выбирается в случае, когда вы хотите поместить результаты в новую книгу; результаты дисперсионного анализа при этом будут размещаться на первом листе новой книги, начиная с ячейки А1.
После установки параметров и нажатия ОК мы получаем матрицу коэффициентов парной корреляции (рис. 4.8).

Никакого анализа на самом деле эта функция не выполняет. Коэффициенты корреляции можно получить и другим способом. Если вы наберете вызовы функций =КОРРЕЛ(A2:A21;B2:B21); =КОРРЕЛ(A2:A21;C2:C21) и =КОРРЕЛ(B2:B21;C2:C21), то в ячейках, где они набраны, получите значения коэффициентов корреляции столбца А с В, А с С и В с С соответственно.
Для принятия решения о наличии значимой связи между переменными необходимо проверить значимость коэффициентов корреляции. Для этого для каждого коэффициента рассчитывается значение t-критерия. В ячейках А25, В25, С25 помещаем формулы =A23*КОРЕНЬ(ЧСТРОК(A2:A22))/КОРЕНЬ(1-A23*A23);
=B23*КОРЕНЬ(ЧСТРОК(B2:B22))/КОРЕНЬ(1-B23*B23) и =C23*КОРЕНЬ(ЧСТРОК(C2:C22))/КОРЕНЬ(1-C23*C23), которые рассчитывают эти значения для rab, rac и rbc соответственно. Критическое значение помещаем в ячейку А27 посредством вызова функции =СТЬЮДРАСПОБР(0,05;ЧСТРОК(A2:A22)-2). Здесь 0,05 — уровень значимости, а ЧСТРОК(A2:A22)-2 — число степеней свободы. Поскольку расчетное значение t-критерия больше критического только для коэффициента корреляции между ОЦП и ОЦК (4,785983 против 2,093025), то этот коэффициент является значимым (остальные два – незначимы).
В ряде случаев для оценки коэффициента корреляции необходимо рассчитывать доверительный интервал. Сначала по формуле (ячейка А27) определяем полуширину доверительного интервала, воспользовавшись формулой =A26*(1-A23*A23)/КОРЕНЬ(ЧСТРОК(A2:A22)). Затем можно найти его нижнюю и верхние границы (=A23-A27 и =A23+A27 соответственно для первого коэффициента корреляции). Результаты приведены на рис. 4.9.

4.2.2. Частная корреляция
Для того чтобы влияние корреляционной связи между двумя переменными «очистить» от возможного влияния третьей, введено понятие частной корреляции. По ней коэффициент корреляции между двумя переменными X и Z определяется по формуле
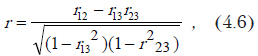
Здесь r12, r13 и r23 — коэффициенты парной корреляции между переменными X и Y, X и Z, Y и X соответственно. При использовании частного коэффициента корреляции необходимо помнить:
- взаимовлияющих переменных может быть не три, а сколь угодно много;
- вы можете не знать о всех взаимовлияющих переменных;
- некоторые авторы утверждают, что для корректного использования частного коэффициента корреляции необходимо наличие многомерного нормального закона распределения, однако проверить выполнение этой предпосылки практически нереально.
Пример
Рассмотрим пример из раздела 4.2.1. В этом примере коэффициент корреляции между ОЦП и ОЦК не очень большой, хотя между ними существует функциональная связь. Возможно это обусловлено влиянием на данные третьей переменной. Попробуем получить коэффициент корреляции между ОЦП и ОЦК, «очистив» его от влияния Ht. Для этого наберем формулу =(A23-B23*C23)/КОРЕНЬ((1-B23*B23)*(1-C23*C23)). В результате получим значение частного коэффициента корреляции между ОЦП и ОЦК — 0,984651. Это значение очень близко к 1 и отвечает нашему интуитивному представлению о функциональной связи.
4.2.3. Ранговая корреляция
Ранговая корреляция является аналогом парной корреляции для тех случаев, когда величины, наличие связи между которыми нужно проверить, представлены не в шкале отношений, а в какой-либо другой. Наиболее часто такая ситуация возникает, если мы имеем дело с субъективными оценками объективных явлений, которые нельзя измерить, то есть с экспертными оценками. Кроме того, ранговая корреляция используется также в случаях, когда закон распределения изучаемых переменных не является гаусовским (нормальным).
Коэффициенты корреляции называются ранговыми, так как перед вычислением значения переменных превращают в ранги. Для этого имеющиеся значения переменных располагают в ранжированном[3] ряду (значения могут в исходном состоянии являться таким ранжированным рядом). Затем каждому значению присваивается ранг от 1 до N, где N — количество анализируемых объектов. В том случае, если несколько элементов имеют один и тот же ранг, то каждому из них присваивается среднее от занимаемых ими мест (см. 3.3.1).
Допущения
- Все наблюдения взаимно независимы.
- Все значения наблюдений извлечены из одной и той же двумерной генеральной совокупности, то есть Х и У одинаково распределены.
Существует несколько различных способов вычисления коэффициентов ранговой корреляции. Наиболее часто используется коэффициент корреляции Спирмена (r, иногда обозначается rs) и коэффициент Кендалла (t).
Коэффициент ранговой корреляции Спирмена
Коэффициент Спирмена вычисляется по формуле
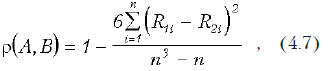
где R1i и R2i — ранги i-го объекта для каждой из сравниваемых переменных. Значение r не зависит от способа упорядочения рангов.
Очевидно, что этот коэффициент является полным аналогом коэффициента парной корреляции — после преобразования его можно представить в виде:
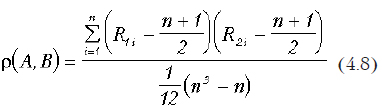
При наличии совпадающих значений (связок) знаменатель уменьшается на величину

где L1 и L2 — количество связок в T1i и T2j — размеры связок (количество элементов в них).
Для проверки значимости коэффициента ранговой корреляции Спирмена при n > 9 можно пользоваться критерием Стьюдента (как и для обычного коэффициента парной корреляции). Проверка значимости для общего случая выполняется с помощью специальных таблиц (см. приложение Е).
Пример
Допустим, нам необходимо проверить, существует ли статистически значимая связь между двумя факторами (признаками), которые являются параметрами гемостазу крови, полученной из локтевой вены у больных со стабильной стенокардией, или эти факторы являются независимыми. Возьмем два фактора, определяющих функциональную активность тромбоцитов: тромбопластиновый (ТФ3) и антигепариновый (ТФ4). Данные и результаты вычислений приведены в табл. 4.2.
Таблица 4.2
Результаты исследования крови у больных со стабильной стенокардией
| ТФ3 | ТФ4 | Ранги ТФ3 (R1) | Ранги ТФ4 (R2) | (R1i – R2i)2 |
| 55 | 72 | 11 | 4 | 49 |
| 24 | 77 | 2 | 5,5 | 12,25 |
| 40 | 85 | 8 | 11 | 9 |
| 60 | 90 | 12 | 13 | 1 |
| 39 | 82 | 7 | 9 | 4 |
| 28 | 77 | 4 | 5,5 | 2,25 |
| 22 | 60 | 1 | 2 | 1 |
| 37 | 79 | 6 | 7 | 1 |
| 72 | 88 | 13 | 12 | 1 |
| 42 | 80 | 10 | 8 | 4 |
| 33 | 66 | 5 | 3 | 4 |
| 41 | 83 | 9 | 10 | 1 |
| 25 | 46 | 3 | 1 | 4 |
| Распределение не нормальное | Распределение нормальное | |||
| Значение суммы квадратов разностей рангов | 93,5 | |||
| Размер выборки | 13 | |||
| Вычисленное значение коэффициента ранговой корреляции Спирмена | 0,743132 | |||
| Уровень значимости a | 0,05 | |||
| Критическое значение по таблице (a = 0,05; N = 13) | 0,412 | |||
Для того, чтобы получить приведенные в табл. 4.2 результаты, необходимо выполнить следующие действия.
- Проверим обе выборки на соответствие их значений нормальному закону распределения. Так как мы располагаем количественными данными, то проверка необходима для того, чтобы определить, каким образом проверять статистическую независимость данных факторов (признаков). Применим пользовательскую функцию NORMSAMP_1(R_1). С этой целью в ячейки B16 и C16 введем соответственно функции =NORMSAMP_1(B3:B15) и =NORMSAMP_1(C3:C15). Результаты покажут, что значения первой выборки не соответствуют нормальному закону распределения (NO_NORM), а второй — соответствуют (NORM). Этот факт позволяет для определения независимости двух признаков (факторов) применить метод ранговой корреляции.
- Построим ранги для первой и второй выборок при помощи пользовательской функции Rank1(x; R_1, t) (см. 3.3.1). Для этого в ячейку D3 введем формулу =Rank1(B3;$B$3:$B$15;0), а в ячейку Е3 — =Rank1(C3;$C$3:$C$15;0). После этого согласованно размножим данные формулы по соответствующим столбцам. В результате этих действий получим ранги первой и второй выборок соответственно (см. рис. 4.10).
- В столбце F получим частичные квадраты разностей рангов первой и второй выборок построчно (R1i – R2i). Для этого в ячейку F3 введем формулу =(D3-E3)^2 и согласованно размножим ее по столбцу.
- Просуммируем квадраты разностей рангов по столбцу F. Для этого в ячейку F17 введем формулу =СУММ(F3:F15). В нашем случае сумма квадратов разностей рангов будет равна 93,5.
- Вычислим коэффициент ранговой корреляции Спирмена, введя в ячейку F19 формулу =1-(6*F17)/(F18^3-F18). Искомый коэффициент будет равен 0,743132.
- Проверим полученный коэффициент ранговой корреляции Спирмена (0,743132) на его статистическую значимость. Для этого, задав уровень значимости a = 0,05, сравним его с табличным значением (приложение Г), которое для такого уровня значимости и размера выборок равно 0,478. Так как вычисленный нами коэффициент ранговой корреляции больше критического (табличного) значения, то нулевая гипотеза о независимости этих двух выборок отвергается. То есть анализируемые нами выборки связаны и довольно тесно.

Коэффициент корреляции Кендалла
Вычисляется по формуле
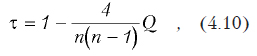
где n — количество наблюдений, а Q — число несогласованных пар (Xj,Yj) и (Xi,Yi) для всех комбинаций i и j. Пары называются несогласованными, если для них выполняется следующее условие:
![]()
где sign — означает «знак». Это функция принимает значение +1 для положительного числа и –1 для отрицательного. Другими словами, приведенное условие означает, что увеличение Х приводит к уменьшению У, и наоборот.
Для проверки значимости коэффициента существуют специальные таблицы (см. приложение Ж).
Пример
Вычислим коэффициент ранговой корреляции Кэндалла, воспользовавшись данными из примера в 4.3.1 (табл. 4.2).
- Проверим обе выборки на соответствие их значений нормальному закону распределения. Так как мы располагаем количественными данными, то проверка необходима для того, чтобы определить, каким образом проверять статистическую независимость данных факторов (признаков). Применим пользовательскую функцию NORMSAMP_1(R_1). С этой целью в ячейки B16 и C16 введем соответственно функции =NORMSAMP_1(B3:B15) и =NORMSAMP_1(C3:C15). Результаты покажут, что значения первой выборки не соответствуют нормальному закону распределения (NO_NORM), а второй — соответствуют (NORM). Этот факт позволяет для определения независимости двух признаков (факторов) применить метод ранговой корреляции.
- Построим ранги для первой и второй выборок при помощи пользовательской функции Rank1(x; R_1, t) (см. 3.3.1). Для этого в ячейку D3 введем формулу =Rank1(B3;$B$3:$B$15;0), а в ячейку Е3 — =Rank1(C3;$C$3:$C$15;0). После этого согласованно размножим данные формулы по соответствующим столбцам. В результате этих действий получим ранги первой и второй выборок соответственно (см. рис. 4.11).
- Вычислим количество инверсий среди рангов второй выборки при условии, что ранги первой выборки согласовано с ней упорядочены. Это означает, что если бы вторая выборка состояла из значений {4, 3, 1,2}, то в ней имелись бы такие инверсии. Для первого элемента: (4 раньше 3) — одна инверсия, (4 раньше 1) — вторая и (4 раньше 2) — третья. Для второго элемента: (3 раньше 1) — одна инверсия и (3 раньше 2) — вторая. Для третьего элемента: (1 раньше 2) — инверсия отсутствует. Таким образом, в этой маленькой выборке {4, 3, 1,2} число инверсий (Q) равно 3+2 = 5.
В нашем примере вычислять подобным образом количество инверсий довольно неудобно, поэтому лучше определить пользовательскую функцию (см. 1.16) подсчета инверсий во второй выборке при условии, что первая согласованно с ней упорядочена. Это функция Candall_K(R_1; R_2), в которой R_1 — массив рангов первой выборки и R_2 — массив рангов второй выборки. Текст функции приведен ниже.
Option Base 1
Function Candall_K(R_1 As Object, R_2 As Object) As Double
‘Вычисление количества инверсий во второй выборке
‘при условии, что первая выборка упорядочена
‘R_1 — 1-й массив (1-я анализируемая выборка)
‘R_2 — 2-й массив (2-я анализируемая выборка)
Dim R_t1()
Dim R_t2()
N_el = R_1.Count ‘вычисление количества элементов в выборке
ReDim R_t1(N_el)
ReDim R_t2(N_el)
‘Формированние временных массивов
For i = 1 To N_el
R_t1(i) = R_1.Cells(i)
R_t2(i) = R_2.Cells(i)
Next i
‘ранжирование первой выборки
‘с согласованной перестановкой второй
Counter = 1 ‘Инициализация индикатора перестановок.
While Counter = 1 ‘ Анализ значения индикатора перестановок.
Counter = 0 ‘Обнуление индикатора перестановок.
For i = 1 To N_el — 1
If R_t1(i) > R_t1(i + 1) Then
tp = R_t1(i): R_t1(i) = R_t1(i + 1): R_t1(i + 1) = tp
Counter = 1
tp2 = R_t2(i): R_t2(i) = R_t2(i + 1): R_t2(i + 1) = tp2
End If
Next i
Wend
‘Подсчет количества инверсий во второй выборке
Sum_K = 0
For i = 1 To N_el — 1
For j = i To N_el — 1
If R_t1(i) < R_t1(j + 1) Then Sum_K = Sum_K + 1
Next j
Next i
Candall_K = Sum_K
End Function
После того, как функция Candall_K(R_1; R_2) будет определена, введите в ячейку Е18 формулу =Candall_K(D3:D15;E3:E15). В результате получим значение количества инверсий Q = 78 (см. рис. 4.11).
- Вычислим коэффициент ранговой корреляции Кендалла, введя в ячейку Е19 формулу =1-4*E18/(E18*(E17-1)). Искомый коэффициент будет равен 0,666667.
- Проверим полученный коэффициент ранговой корреляции Кендалла (0,666667) на его статистическую значимость. Для этого, задав уровень значимости a = 0,05, сравним его с табличным значением (приложение Д), которое для такого уровня значимости и размера выборок равно 0,359. Так как вычисленный нами коэффициент ранговой корреляции больше критического (табличного) значения, то нулевая гипотеза о независимости этих двух выборок отвергается. То есть анализируемые нами выборки связаны и довольно тесно.

Замечания к коэффициентам Кендалла и Спирмена
- Рассчитанные для одних и тех же данных значения коэффициентов Кендалла и Спирмена не совпадают, кроме крайних значений (–1,0,1).
- Асимптотически эти коэффициенты сходятся.
Конкордация
В том случае, когда необходимо сравнение не двух переменных, а большего количества (например, при выяснении согласованности мнений группы экспертов) используется коэффициент конкордации, предложенный Кендаллом:
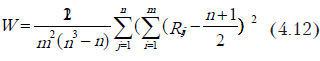
где n — количество анализируемых объектов, m — количество экспертов, Rij — ранг j-го объекта, который присвоен ему i-ым экспертом.
Следует обратить внимание на отличие в значениях коэффициента конкордации от коэффициента корреляции. Если мнения экспертов полностью противоположны, коэффициент конкордации равен нулю (W = 0), но коэффициент корреляции в этом случае будет равен –1.
При наличии связок (одинаковых значений) формула приобретает следующий вид
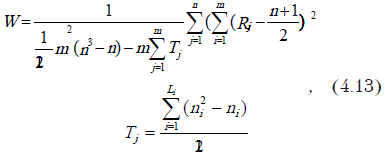
где , при этом Li – число связок, ni количество элементов в i-й связке для j-го эксперта.
Значимость коэффициента конкордации при малом количестве экспертов проверить затруднительно. Для малых значений существуют неполные таблицы, например таблица 6.10 в [1], фрагмент из которой приведен ниже.
Таблица 4.3
| N=3;m=10 | N=5;m=3 | ||
| 50 | 0,092 | 56 | 0,096 |
| 62 | 0,046 | 62 | 0,056 |
| 104 | 0,0034 | 78 | 0,053 |
| 126 | 0,0008 | 86 | 0,0009 |
Для получения критического значения коэффициента конкордации необходимо взятое из таблицы значение подставить в формулу: 12*S/m2(n3–n).
Если же количество экспертов больше 7, то возможно сравнение значения выражения n(m-1)W с табличным значением, распределенным по c2 с N-1 степенями свободы.
Пример
Есть 7 объектов, каждый из которых оценивается независимо тремя экспертами по десятибальной шкале (см. рис. 4.12, ячейки В2–Е9). Необходимо определить степень согласованности мнений экспертов – коэффициент конкордации.
- Рассчитываем столбцы для выражения . Для этого в ячейку G3 помещаем формулу =Rank1(C3;C$3:C$9;1)-(ЧСТРОК(C$3:C$9)-1)/2. Затем размножаем ее от G3 до I
- Формируем столбец построчных сумм квадратов. Для этого в ячейку J3 помещаем формулу =СУММ(G3:I3)*СУММ(G3:I3), которую затем размножаем перетягиванием до
- Находим сумму по столбцу, для чего в ячейку J10 вводим формулу =СУММ(J3:J9).
- В ячейки J11 и J12 вводим число экспертов m =ЧИСЛСТОЛБ(C3:E3) и число объектов n =ЧСТРОК(C3:C9).
- Рассчитываем значение коэффициента конкордации
=12*J10/(J11*J11*(J12*J12*J12-J12)).
Как видно из величины коэффициента конкордации (0,674603), согласованность между экспертами существует, хотя и не очень большая (см. рис. 4.12).

4.3. Дисперсионный анализ
В задачах, которые решаются дисперсионным анализом присутствует отклик числовой природы, на который воздействует несколько переменных, имеющих номинальную природу. Например, несколько видов рационов откорма скота или два способа их содержания и т.п. Считается, что мы можем рассматривать модель
![]()
то есть рассеивание равно изменению, зависящему от одного фактора , плюс рассеивание, зависящее от второго фактора , плюс случайная ошибка . Тогда общее рассеяние состоит из нескольких компонент: s2 = s2a + s2b + s2. Выделив соответствующие компоненты, с помощью критерия Фишера можно определить их значимость.
4.3.1. Параметрический дисперсионный анализ
Однофакторная задача
Для простейшего случая таблица исходных данных имеет следующий вид:
Таблица 4.4
Общий вид исходных данных для однофакторного дисперсионного анализа
| Номера элементов совокупностей | 1 | 2 | … | j | … | n |
| Номера совокупностей | ||||||
| 1 | X11 | X12 | X1j | X1n | ||
| 2 | X21 | X22 | X2j | X2n | ||
| … | … | … | ||||
| I | Xi1 | Xi2 | Xij | Xjn | ||
| … | … | … | ||||
| m | Xm1 | Xm2 | Xmj | Xmn |
Это может быть, например, m партий сырья, и из каждой взято n образцов. Необходимо выяснить, изменяются ли показатели сырья от партии к партии. Мы можем также рассматривать какие-то характеристики лабораторных животных (m групп по n животных в каждой), чтобы выяснить, отличаются ли их характеристики от группы к группе. Смысл в том, чтобы сравнить дисперсию, обусловленную случайными причинами, с дисперсией, вызываемой наличием некоторого фактора. Если они значимо различаются, то фактор оказывает статистически значимое влияние на исследуемую переменную.
Отличие считается значимым, если расчетное значение критерия Фишера (отношение межгрупповой дисперсии к внутригрупповой) будет больше табличного, взятого с заданным уровнем значимости и степенями свободы (m-1) и m(n-1).
Межгрупповая дисперсия рассчитывается по формуле
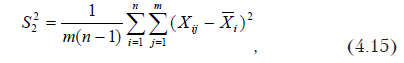
Внутригрупповая —

Здесь — общее среднее, а .
Для дисперсионного анализа в английском языке принято сокращение ANOVA (ANalys Of VAriances, что означает «дисперсионный анализ»), которое используется и в некоторых русскоязычных источниках.
Для однофакторного случая результаты расчетов принято представлять в следующем виде (см. табл. 4.5).
Таблица 4.5
Представление результатов расчета однофакторного дисперсионного анализа
| Компоненты дисперсии | Сумма квадратов | Число степеней свободы | Средний квадрат
(дисперсия) |
| Межгрупповая (влияющий фактор) | m-1 | ||
| Внутригрупповая
(случайное влияние) |
m(n-1) | ||
|
Общая |
mn-1 |
Здесь внутригрупповая дисперсия характеризует влияние случайной составляющей, а межгрупповая — влияние изучаемого фактора.
Пример
Пример условный, но базируется на реальной задаче, приведенной в [6], в которой рассматривается влияние погоды на изменение продолжительности систолической остановки сердца при введении бария хлорида. Допустим (см. таблицу 4.6), у нас есть набор данных, которые характеризуют продолжительность реакции лабораторных животных на некоторый препарат при различных погодных условиях.
Таблица 4.6
Исходные данные примера однофакторного дисперсионного анализа
| Экспериментальные животные | ||||
| Погода | 1 | 2 | 3 | 4 |
| Тихая погода | 13,8 | 11 | 13,7 | 12,1 |
| Ветер и вьюга | 16 | 12,2 | 15,8 | 14,3 |
После того как наши данные набраны в электронной таблице (строки 2–4 и столбцы А — Е), входим в меню, выбирая последовательно Сервис, а затем Анализ данных, в результате чего появится окно (см. рис.4.13).
В этом окне необходимо выбрать «Однофакторный дисперсионный анализ». После чего откроется новое окно (см. рис. 4.14).
В этом окне необходимо задать исходные данные для дисперсионного анализа.
Входной интервал — необходимо отметить таблицу, в которой размещены исходные данные (левая верхняя ячейка и правая нижняя).
Группирование — необходимо указать, в строках или столбцах находятся данные, относящиеся к одному уровню фактора (в данной ситуации — в строках).
Альфа — требуемый уровень значимости.
Выходной интервал — вводится ссылка на ячейку, расположенную в левом верхнем углу выходного диапазона (мета, куда вы хотите поместить результат). Размеры выходной области будут рассчитаны автоматически.
Новый рабочий лист — выбирается в том случае, когда вы хотите поместить результаты работы на другой лист; при этом в соответствующем окошке указывается диапазон размещения результатов аналогично предыдущему пункту.
Новая рабочая книга — выбирается, если вы хотите поместить результаты в новую книгу; результаты дисперсионного анализа при этом будут размещаться на первом листе новой книги, начиная с ячейки А1.
Исходные данные и результаты для нашего примера приведены на рисунке 4.15.

Здесь
SS — сумма квадратов;
Между группами — межгрупповая сумма квадратов;
Внутри групп — внутригрупповая сумма квадратов;
Итого — общая (полная) сумма квадратов;
df — число степеней свободы;
MS — средний квадрат (фактически дисперсия);
F — расчетное значение критерия Фишера;
P-Значение — расчетное значение минимальной значимости;
F критическое — критическое значение распределения Фишера.
В нашем примере расчетное значение критерия Фишера (3,026) меньше критического (5,99). Из этого следует, что мы принимаем гипотезу об отсутствии влияния погоды на фармакологические реакции при принятом уровне значимости 0,05.
P-Значение в нашем примере равно 0,133. Поскольку оно достаточно велико, нет оснований отвергать гипотезу о равенстве дисперсий.
Замечание к дисперсионному анализу в Excel
В функции дисперсионного анализа в Excel проверяется следующая альтернативная гипотеза: дисперсия числителя больше дисперсии знаменателя, то есть односторонняя гипотеза. При этом не учитывается возможность ситуации, когда F-расчетное меньше 1. В таком случае выполняемая в Excel односторонняя проверка с критическим значением распределения Фишера неправомочна (см. 3.2.1). Для корректной проверки необходимо или пересчитать расчетное и критическое значение критериев Фишера и после этого выполнить их сравнение или же рассчитать нижнюю критериальную границу.
Допустим, что подобная ситуация возникла в нашем примере (то есть расчетное значение критерия меньше 1). Тогда новое значение расчетного значения F-критерия определяется по формуле =1/F16, а соответствующее ему критическое значение — из функции = FРАСПОБР(0,05;D17;D16). Если новое расчетное значение больше нового критического, то гипотеза о равенстве дисперсий отклоняется и принимается гипотеза о том, что внутригрупповая дисперсия больше межгрупповой.
Для второго варианта проверки расчетное критическое значение не изменяется, но рассчитываются новые значения для критериальных границ: нижней =FРАСПОБР(0,972; D16;D17) и верхней = FРАСПОБР(0,972; D16;D17). Если расчетное критическое значение находится внутри этих границ, то гипотеза об отсутствии различия принимается. Если расчетное значение больше верхнего или меньше нижнего, тогда принимается альтернативная гипотеза, которая в данном случае звучит так: межгрупповая и внутригрупповая дисперсия различаются статистически значимо.
Однофакторная задача с неравномерным числом испытаний
Достаточно часто возникает ситуация, при которой число опытов для разных значений уровня фактора различно. Это может быть связано, например, с тем, что часть лабораторных животных во время эксперимента погибла или не проявила требуемой реакции и пр.
Тогда общая дисперсия определяется по формуле
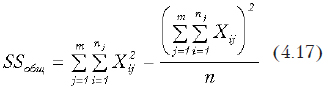
где Xij — значение соответствующего наблюдения аналогично указанному в предыдущем параграфе, nj — количество наблюдений для j-го уровня фактора; — общее количество наблюдений.
Межгрупповая (вызванная влиянием фактора) сумма квадратов определяется по формуле
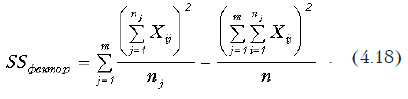
Остаточная сумма находится как разница между общей и факторной
SSост = Ssобщ – SSфактор
Затем находятся остаточная (внутригрупповая) и факторная (межгрупповая) дисперсии , а также расчетное значение критерия Фишера .
Примечание:
- В однофакторном дисперсионном анализе Excel данный вариант не предусмотрен.
Пример
Рассмотрим пример, использованный в предыдущей задаче, но с меньшим количеством (равным трем) наблюдений для погоды.
Проведем вспомогательные вычисления.
Таблица 4.7
Формулы вспомогательных вычислений
| Ячейка | Содержание | Комментарий |
| В5 | =ЧСТРОК(B3:B4) | Число уровней варьирования фактора |
| от В6 до Е7 | =B3*B3 в В6, остальные размножаются | Квадраты значений наблюдений |
| от F3 до F4 | =СУММ(B3:E3) в F3, далее размножается | Сумма значений наблюдений |
| от G3 до G 4 | =ЧИСЛСТОЛБ(B3:E3) в G3, далее размножается | Количество наблюдений в каждой строке |
| от H3 до H4 | =F3*F3/G3 в H3, далее размножается | Квадраты сумм, деленные на число наблюдений |
После этого мы можем рассчитывать значения, которые непосредственно входят в таблицу дисперсионного анализа. В таблице 4.8 приведены формулы (с соответствием размещения по ячейкам), по которым и выполняется расчет всех необходимых промежуточных значений. Как обычно, однотипные формулы набираются один раз, а затем размножаются (см. раздел 1).
Таблица 4.8
Формулы для формирования вспомогательной таблицы
| A | B | C | D | E | |
| 9 | = СУММ(H3:H4)-СУММ(F3:F4)*СУММ(F3:F4)/СУММ(G3:G4) | =ЧСТРОК(B3:B4)-1 | =B9/C9 | =D9/D10 | =FРАСПОБР(0,05;C9;C10) |
| 10 | =B11-B9 | =СУММ(G3:G4)-B5 | =B10/C10 | =D9/D10 | |
| 11 | =СУММ(F6:F7)-СУММ(F3:F4)*СУММ(F3:F4)/СУММ(G3:G4 |
В табл. 4.9, соответствующей по размещению табл. 4.7, приведено описание содержания ячеек.
Таблица 4.9
Описание содержимого ячеек для таблицы 4.8
| A | B | C | D | E | |
| 9 | Сумма квадратов, обусловленная влиянием фактора | Число степеней свободы для дисперсии, обусловленной влиянием фактора | Дисперсия, обусловленная влиянием фактора | Расчетное значение критерия Фишера | Критическое значение распределения Фишера |
| 10 | Сумма квадратов, обусловленная влиянием случайной составляющей | Число степеней свободы для дисперсии, обусловленной влиянием случайной составляющей | Дисперсия, обуслов-ленная влиянием случайной составляющей | ||
| 11 | Общая сумма квадратов |
Результаты работы приведены на рис. 4.16. Из него видно, что, поскольку расчетное значение критерия Фишера меньше критического, следовательно влияние фактора отсутствует.
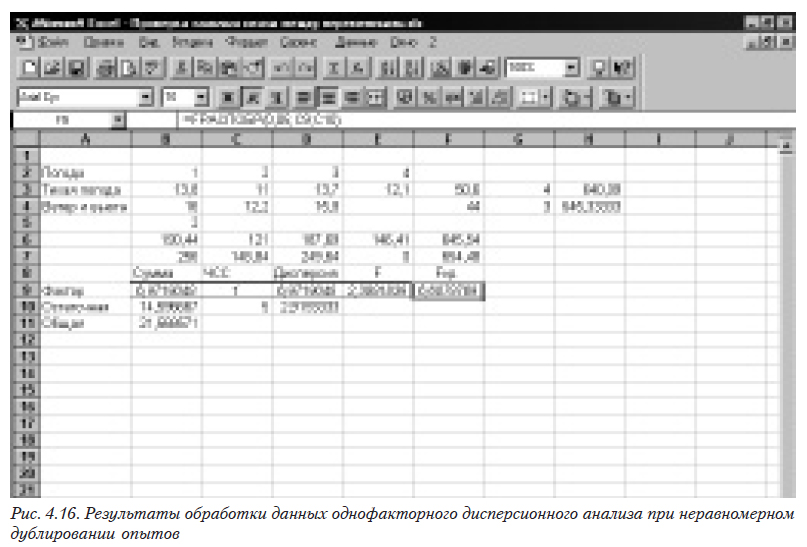
Двухфакторная задача с равномерным числом наблюдений в ячейке
В такой задаче есть два фактора, измеряемых в шкале наименований, которые влияют на отклик. Общий вид представления данных для такой задачи содержится в табл. 4.10.
Таблица 4.10
Общий вид представления данных для двухфакторного дисперсионного анализа
| Фактор | Фактор В | ||||
| А | В1 | В1 | … | Вn | |
| A1 | Х111, Х112,… Х11k | Х121, Х122,… Х12k | … | Х1n1, Х1n2,… Х1nk | |
| A2 | Х211, Х212,… Х21k | Х221, Х222,… Х22k | … | Х2n1, Х2n2,… Х2nk | |
| : | … | … |
Хij1, Хij2,… Хijk |
… | |
| Am | Хm11, Хm12,… Хm1k | Хm21, Хm22,… Хm2k | … | Хmn1, Хmn2,… Хmnk | |
| … | |||||
Здесь Х111, Х112,… Хmnk — наблюдавшиеся значения исследуемой переменной; — среднее значение в ячейке; — среднее значение по строке; — среднее по столбцу; — общее среднее. Результаты расчетов обычно представляются в таблице следующего вида.
Таблица 4.11
Форма представления результатов двухфакторного дисперсионного анализа
| Компонента дисперсии | Суммы квадратов | Число степеней свободы | Дисперсии |
| Между средними по строкам (по фактору А) | n-1 | ||
| Между средними по столбцам (по фактору В) | m-1 | ||
| Взаимодействие | (m-1)(n-1) | ||
| Остаточная | nm(k-1) | ||
| Полная | nmk-1 |
Здесь — характеризует влияние фактора А; — влияние фактора В; — совместное влияние обоих факторов; — влияние случайных факторов, которые невозможно отнести ни к А, ни к В. Необходимо проверить значимость различия дисперсий и , и , и .Для этого находят расчетные значения F критерия Фишера FA=/, FB=/, FAB=/. Если выполняются условия (каждое отдельно!) FA >Fa,n-1,nm(k-1), FB >Fa,m-1,nm(k-1), FAB >Fa,,(n-1)(m-1),nm(k-1) то влияние факторов А, В (или их взаимодействия соответственно) является значимым.
В Excel есть два варианта двухфакторного регрессионного анализа: с повторениями и без повторений. Двухфакторный дисперсионный анализ с повторениями соответствует описанному выше в данном параграфе. Двухфакторный дисперсионный анализ без повторений — такая его разновидность, в каждой ячейке которого содержится только одно наблюдение. Таблица исходных данных для такого анализа имеет вид, подобный таблице однофакторного, только вместо номера испытания — номер уровня второго фактора. Таблица результатов похожа на приведенную выше таблицу, только в ней отсутствует строка взаимодействия факторов.
К сожалению, функция двухфакторного дисперсионного анализа с повторениями в Excel работает неправильно и выполнять расчеты по ней невозможно.
Пример
Сначала рассмотрим пример двухфакторного дисперсионного анализа без повторений.
(Пример условный). Допустим, что необходимо выяснить, не оказывает ли значимое влияние на изучаемую характеристику личность экспериментатора и питомник, из которого получают животных для лабораторных исследований. A priori предполагается, что не оказывают.
Таблица 4.12
Исходные данные для двухфакторного дисперсионного анализа без повторений
| Экспериментатор | Питомник 1 | Питомник 2 | Питомник 3 |
| A | 75 | 67 | 78 |
| B | 68 | 65 | 59 |
| C | 56 | 69 | 65 |
Поместив данные в таблицу Excel выбираем в меню Сервис, Анализ данных. Появится окно (см. рис. 4.13), в котором выбираем «Двухфакторный дисперсионный анализ без повторений». После этого появляется окно установки параметров (рис. 4.17).
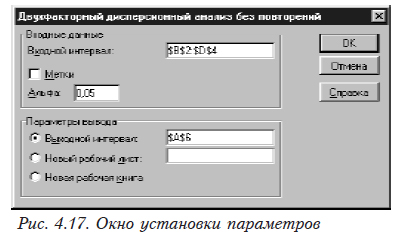
Здесь
Входной интервал — ссылка на левую верхнюю и правую нижнюю ячейки таблицы, в которых находятся данные. Могут быть отмечены мышкой.
Альфа — требуемый уровень значимости.
Выходной интервал — вводится ссылка на ячейку, расположенную в левом верхнем углу выходного диапазона(мета, куда вы хотите поместить результат). Размеры выходной области будут рассчитаны автоматически.
Новый рабочий лист — выбирается в том случае, если вы хотите поместить результаты работы на другой лист (при этом в соответствующем окошке указывается диапазон размещения результатов аналогичный указанному в предыдущем пункте).
Новая рабочая книга — выбирается в том случае, когда вы хотите поместить результаты в новую книгу (результаты дисперсионного анализа при этом будут размещаться на первом листе новой книги, начиная с ячейки А1).
После установки всех необходимых параметров выбирается ОК. Результаты работы представлены на рис. 4.18.
Здесь
SS — сумма квадратов;
Строки — сумма квадратов, обусловленная первым фактором (изменением по строкам);
Столбцы — сумма квадратов, обусловленная вторым фактором (изменением по столбцам);
Погрешность — остаточная сумма квадратов, обусловленная случайной ошибкой;
df — число степеней свободы;
MS — средний квадрат (фактически дисперсия);
F — расчетное значение критерия Фишера;
P-Значение — расчетное значение минимальной значимости;
F критическое — критическое значение распределения Фишера.
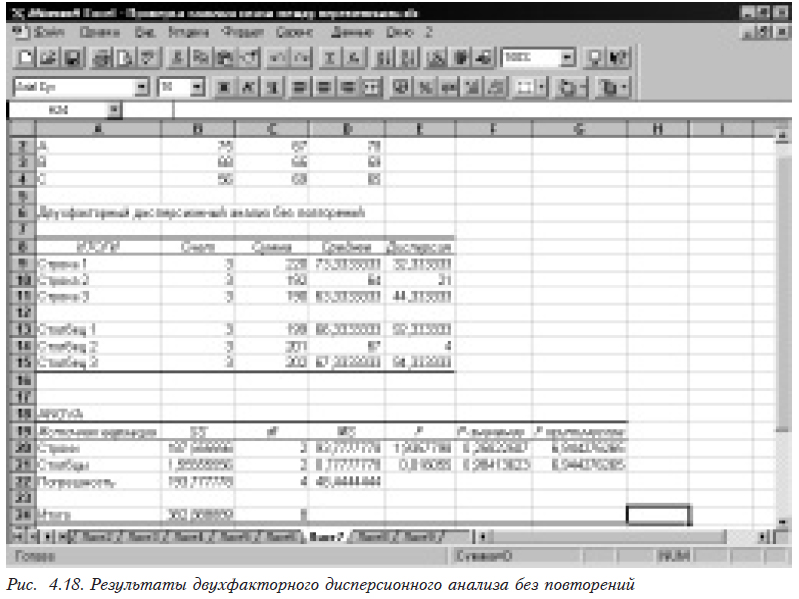
Для первого фактора (строки) F-расчетное (1,93578) меньше критического 6,944276. Это заставляет принять нас нулевую гипотезу о равенстве дисперсий, следовательно, первый фактор не влияет на изучаемый показатель. Что касается второго фактора (столбцы), то здесь расчетное значение критерия Фишера меньше 1 (0,016055), и проверка в том виде, который приведен в Excel, некорректна.
Проверка может быть осуществлена двумя способами.
Первый способ. Проверяется односторонний критерий: одна дисперсия больше другой. Для этого находим обратное значение к имеющемуся расчетному значению =1/E21 (получим 62,28571), а затем — новое критическое значение =FРАСПОБР(0,05;C22;C21), в котором степени свободы поменялись местами (получили 19,24673). Поскольку расчетное больше критического, то принимается гипотеза, что дисперсия погрешности больше дисперсии столбцов.
Второй способ. Не изменяя расчетное значение критерия Фишера, рассчитываем новые критические значения для проверки двухсторонней альтернативной гипотезы (дисперсии неравны). Нижнее критическое при этом вычисляется по формуле =FРАСПОБР(0,975;C21;C22) (результат равен 0,025475), а верхнее — по формуле =FРАСПОБР(0,025;C21;C22) (результат равен 10,64905). Поскольку 0,016055 меньше 0,025475, то гипотеза о неравенстве дисперсий принимается. При этом дисперсия, вызванная случайными факторами, больше.
Двухфакторный дисперсионный анализ с повторениями
Исходные данные для анализа представлены в табл. 4.13. Каждый опыт (для каждого экспериментатора) был сделан 3 раза.
Таблица 4.13
Исходные данные для двухфакторного дисперсионного анализа
| Экспериментатор | Питомник 1 | Питомник 2 | Питомник 3 |
| 75 | 67 | 78 | |
| А | 68 | 65 | 59 |
| 56 | 69 | 65 | |
| 66 | 76 | 55 | |
| Б | 67 | 87 | 57 |
| 78 | 67 | 69 | |
| 78 | 56 | 67 | |
| В | 56 | 78 | 67 |
| 58 | 80 | 67 | |
| 74 | 67 | 77 | |
| Г | 73 | 54 | 66 |
| 71 | 78 | 72 |
Исходные данные вводятся в Excel и содержатся в ячейках от А1 до D13 (см. рис. 4.19). Выполняем следующие действия.
- Вычисляем , которые размещаем в ячейках от В16 до D20.
- Вычисляем средние значения по строкам .
- Вычисляем средние значения по столбцам .
- Вычисляем общее среднее .
Формулы, использованные для вычислений, представлены в таблице 4.14
Таблица 4.14
Формулы для вычисления средних, набранные в Excel
| Ячейка | B | C | D | E |
| 16 | =СРЗНАЧ(B$2:B$4) | =СРЗНАЧ(C$2:C$4) | =СРЗНАЧ(D$2:D$4) | =СРЗНАЧ($B16:$D16) |
| 17 | =СРЗНАЧ(B$5:B$7) | =СРЗНАЧ(C$5:C$7) | =СРЗНАЧ(D$5:D$7) | =СРЗНАЧ($B17:$D17) |
| 18 | =СРЗНАЧ(B$8:B$10) | =СРЗНАЧ(C$8:C$10) | =СРЗНАЧ(D$8:D$10) | =СРЗНАЧ($B18:$D18) |
| 19 | =СРЗНАЧ(B$11:B$13) | =СРЗНАЧ(C$11:C$13) | =СРЗНАЧ(D$11:D$13) | =СРЗНАЧ($B19:$D19) |
| 20 | =СРЗНАЧ(B$16:B$19) | =СРЗНАЧ(C$16:C$19) | =СРЗНАЧ(D$16:D$19) | =СРЗНАЧ(E16:E19) |
Набрать можно не все формулы, а только часть — остальные получим путем размножения перетягиванием. Необходимо набрать формулы в столбец В от 16 до 20 строчки, а формулы в столбцах С и D получим построчным перетягиванием ячеек столбца В. В столбце Е набираем ячейку Е16, а ячейки Е17–Е19 получаем перетягиванием. Ячейка Е20 набирается вручную, причем безразлично получите ли вы в ней сумму по строкам или по столбцам. Это будет одно и то же значение.
- Находим квадраты разностей для каждой ячейки. Массив разностей размещен в ячейках с F2 по
Для этого размещаем формулы
| Ячейка | Содержимое |
| F2 | =(B2-B$16)*(B2-B$16) |
| F5 | =(B5-B$17)*(B5-B$17) |
| F8 | =(B8-B18)*(B8-B18) |
| F11 | =(B11-B$19)*(B11-B$19) |
В остальных ячейках формулы размножаются перетягиванием. При этом в столбце F ячейки размножаются сверху вниз, а столбцы G и H получаем построчным перетягиванием соответствующих ячеек столбца F.
- Находим квадраты построчных разностей . Для этого в ячейке G16 помещаем формулу =(E16-$E$20)*(E16-$E$20), которую затем размножаем на ячейки G17–G19 перетягиванием.
- Находим квадраты разностей по столбцам . Для этого в ячейку В22 помещаем формулу =(B20-$E$20)*(B20-$E$20), которую затем размножаем построчно на ячейки С и D.
- Находим квадраты разностей, необходимые для расчета дисперсии взаимодействия . Для этого в ячейку И25 помещаем формулу =(B16+$E$20-B$20-$E16)*(B16+$E$20-B$20-$E16), которую размножаем на все ячейки таблицы до D28 перетягиванием.
- Формируем таблицу дисперсионного анализа (ячейки от G21 до N25).
Таблица по содержанию в основном соответствует таблице 4.11. Отличие состоит в отсутствии строки для полной суммы квадратов. Дополнительно есть столбцы для расчетного значения критерия Фишера нижнего и верхнего критического значения для проверки гипотезы. Расчетные формулы, которые помещены в ячейки, представлены в табл. 4.15 и 4.16.
Таблица 4.15
| Ячейка | I | J | K | L |
| 22 | =СУММ(G16:G19)*ЧИСЛСТОЛБ(B2:D2)*ЧСТРОК(B2:B4) | =(ЧИСЛСТОЛБ(B2:D2)-1) | =I22/J22 | =K22/$K$25 |
| 23 | =СУММ(B22:D22)*4*ЧСТРОК(B2:B4) | =4-1 | =I23/J23 | =K23/$K$25 |
| 24 | =ЧСТРОК(B2:B4)*СУММ(B25:D28) | =(4-1)*(ЧИСЛСТОЛБ(B2:D2)-1) | =I24/J24 | =K24/$K$25 |
| 25 | =СУММ(F2:H13) | =4*ЧИСЛСТОЛБ(B2:D2)*(ЧСТРОК(B2:B4)-1) | =I25/J25 |
Таблица 4.16
| Ячейка | M | N |
| 22 | =FРАСПОБР(0,975;$J22;$K$25) | =FРАСПОБР(0,025;$J22;$K$25) |
| 23 | =FРАСПОБР(0,975;$J23;$K$25) | =FРАСПОБР(0,025;$J23;$K$25) |
| 24 | =FРАСПОБР(0,975;$J24;$K$25) | =FРАСПОБР(0,025;$J24;$K$25) |
Все три расчетных значения критерия Фишера меньше нижней критической границы. Поэтому принимается гипотеза о значимом превышении остаточной дисперсии над дисперсиями строк, столбцов и взаимодействий. Это значит, что в данном примере влияние экспериментатора и питомника значимо меньше влияния неизвестных нам случайных факторов. Если бы это были результаты реального эксперимента, то из статистического анализа вытекает вывод:
- Результаты экспериментов фальсифицированы, то есть рассеяние от влияющих факторов слишком мало. Или оно должно быть больше рассеяния случайных факторов (при наличии влияния факторов), или не должно отличаться от них (при отсутствии влияния). В данном случае результаты фальсифицированы.
- Эксперимент проведен некачественно. На результаты опытов влиял фактор (или несколько факторов), который мы не учитывали.

Примечание:
- Существуют более сложные схемы, учитывающие большее количество факторов, их взаимодействия и возможность повторных опытов, неравномерность числа наблюдений в ячейке и пр.
- Следует отметить, что с ростом количества компонент расчеты и анализ становятся более громоздкими. При числе факторов больше двух возможно использование (с некоторыми ограничениями) регрессионного анализа.
4.3.2. Непараметрический дисперсионный анализ Фридмана
Назначение. В том случае, когда закон распределения не является нормальным, используется непараметрический дисперсионный анализ Фридмана.
Нулевая гипотеза. Средние значения всех выборок равны.
Предпосылки
- Все случайные величины взаимно независимы.
- Данные каждой выборки распределены по одному закону распределения. Обратите внимание: закон распределения каждой выборки может отличаться от закона распределения других.
Описание метода
Исходные данные представляются в следующем виде (табл. 4.17).
Таблица 4.17
Общий вид исходных данных для однофакторного дисперсионного анализа
| Номера элементов совокупностей | 1 | 2 | … | j | … | n |
| Номера совокупностей | ||||||
| 1 | X11 | X12 | X1j | X1n | ||
| 2 | X21 | X22 | X2j | X2n | ||
| … | … | … | ||||
| I | Xi1 | Xi2 | Xij | Xjn | ||
| … | … | … | ||||
| m | Xm1 | Xm2 | Xmj | Xmn |
Для этого в каждом столбце значения Х заменяют их рангами (другими словами, вместо значений переменных ставится их номер в ряду, упорядоченном по возрастанию). Затем рассчитывается значение критерия:

где Rij — соответствующие значения рангов.
Если расчетное значение c2 будет больше критического, взятого с заданным уровнем значимости и (n-1) степенью свободы, гипотеза о различии между партиями принимается.
При расчетах можно проверить правильность расстановки рангов и расчетов, зная, что имеет место соотношение
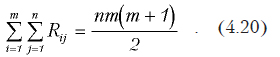
Прмечание:
- При малых значениях m и n критерий c2 дает слишком грубое приближение, и при этом возможно принятие неправильного решения. Поэтому критерий c2 применяется в том случае, когда выполняются следующие условия: m = 3 и n > 9 или m = 4 и n > 4 или m > 4 n ³ 9 (см. [4]). Если эти условия не выполняются, то проверка осуществляется по критерию Фридмана (см. табл. в приложении Б).
Пример.
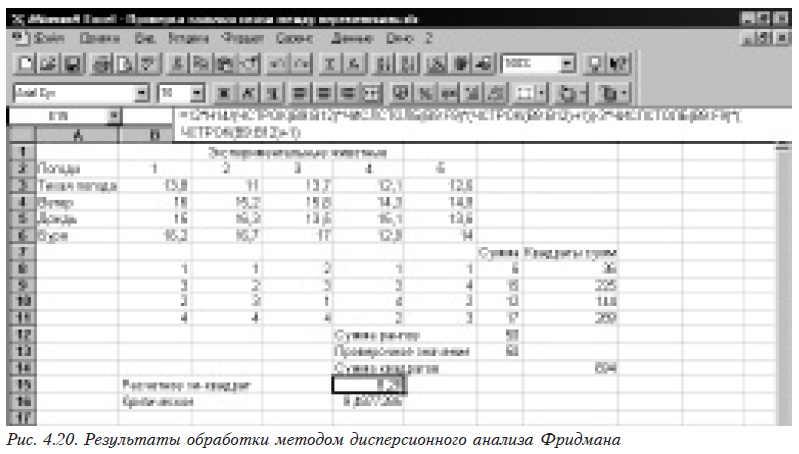
Рассмотрим вариант примера, использованного в 4.3.1 (данные изменены и расширены): у нас есть 4 вида погодных условий, для каждого из которых проведено 5 экспериментов. Необходимо выяснить, значимо ли влияет изменение погодных условий на результаты экспериментов. Все исходные данные и результаты работы приведены на рис. 4.20.
Сначала необходимо построить ранги по столбцам. Для этого в ячейке В8 набираем вызов функции построения рангов =Rank1(B3;B$3:B$6;1), а затем размножаем ее перетягиванием на ячейки от В8 до F11.
Находим суммы рангов по строкам и помещаем их в столбец G. Для этого в G8 набираем формулу =СУММ(B8:F8), а потом размножаем ее перетягиванием на остальные ячейки столбца. Здесь желательно выполнить проверку расстановки рангов. Для этого в ячейке G12 формируем сумму рангов (=СУММ(G8:G11)), а в ячейке G13 — проверочное значение, которое определяется по формуле
=(ЧСТРОК(B9:B12)*ЧИСЛСТОЛБ(B9:F9)*(ЧСТРОК(B9:B12)+1))/2.
Если эти значения совпадают, то расчеты выполнены правильно.
Далее в столбце H формируем квадраты сумм рангов по строчкам. Для этого в ячейке H8 набираем формулу =G8*G8 и размножаем перетягиванием на остальные ячейки столбца.
Находим сумму квадратов =СУММ(H8:H11) и помещаем ее в ячейке H14.
Теперь мы можем рассчитать критериальное значение по формуле
=12*H14/(ЧСТРОК(B8:B11)*ЧИСЛСТОЛБ(B8:F8)*(ЧСТРОК(B8:B11)+1))-3*ЧИСЛСТОЛБ(B8:F8)*(ЧСТРОК(B8:B11)+1) и определить критическое значение критерия c2 вызовом функции
=ХИ2ОБР(0,05;ЧСТРОК(B8:B11-1)).
Поскольку расчетное критериальное (8,28) меньше критического (9,4877), то принимается гипотеза об отсутствии значимого влиянии погодных условий на результаты эксперимента.
4.4. Анализ таблиц сопряженности
–Анализ показывает, что Ежов и Бочаров ни разу не встречались вместе в одном ресторане, одном театре, одном санатории…но статистика показывает, что таких чисто официальных отношений между Ежовым и его подчиненными не бывает.
–Вы можете свою мысль выразить короче?
–Заговор.
Виктор Суворов “Контроль”
В медико-биологических исследованиях большую роль играет анализ таблиц сопряженности.
Для этих методов применяют также название «анализ таблиц долей и пропорций». Предназначены методы для анализа данных, которые описывают объекты с некоторым количеством свойств, причем часто о свойстве можно лишь сказать есть оно или нет (например, см. таблицу из [21] — табл. 4.18).
Таблица 4.18
Показатели смертности от рака легких и ишемической болезни сердца (на 100000 человек в год)
| Заболевание | Курящие | Некурящие |
| Рак легких | 48,33 | 4,49 |
| Ишемическая болезнь сердца | 394,67 | 109,54 |
Нулевая гипотеза показатели смертности от указанных заболеваний не зависит от того, курит человек или нет. Если нулевая гипотеза будет отвергнута, то это означает, что между курением и смертностью от указанных заболеваний существует статистически значимая связь.
4.4.1.Четырехклеточные таблицы
В общем виде четырехклеточная таблица (их еще называют таблицы 2Х2) имеет следующий вид (табл. 4.19).
Таблица 4.19
Общий вид четырехклеточной таблицы сопряженности
| Выборки | Наличие признака | Отсутствие признака | Итого |
| Первая выборка | A | B | n1 = A + B |
| Вторая выборка |
C |
D | n2 = C + D |
| Итого | A + C | B + D | n = n1 + n2 |
Нулевая гипотеза о принадлежности обеих выборок к одной генеральной совокупности выполняется с использованием критерия c2, который рассчитывается по формуле

Для малых выборок вместо n берут (n-1).
Расчетное значение сравнивается с критическим, взятым с одной степенью свободы и заданным уровнем значимости. Если расчетное значение больше критического, то гипотезу об однородности следует отбросить и принять гипотезу о наличии между изучаемыми признаками существенной связи.
Примечание:
- Правильность полученных выводов зависит от того, как были выбраны данные: выборка должна быть однородна по отношению к анализируемому признаку. Например, если в анализируемую выборку входят одновременно особи, на которых препарат оказывает положительное (улучшающее состояние здоровья) влияние, и особи, на которых он оказывает отрицательное влияние, то в результате анализа может быть принята гипотеза о том, что препарат не оказывает никакого влияния. А это не соответствует реальному положению вещей.
- Следует помнить, что объем выборок не должен быть слишком маленьким. Так, для уровня значимости 0,05 необходимо минимальное значение n1= n2 = 124 (n = 248).
Кроме четырехклеточных таблиц сопряженности существуют многоклеточные таблицы сопряженности. Использование каждого вида таблицы сопряженности в качестве данных для регрессионного анализа будет рассмотрено в соответствующих параграфах.
Пример
Рассмотрим анализ на примере задачи, представленной таблицей 4.16. На рис. 4.21 представлены исходные данные. Для решения задачи о проверки наличия связи между курением и смертностью от рака легких и ишемической болезни сердца выполним следующие действия.
- Найдем суммы по строчкам и по столбцам, для чего введем формулы суммирования в соответствующие ячейки.
| Строка/Столбец | C | D | E |
| 3 | 48,33 | 4,49 | =СУММ(C3:D3) |
| 4 | 394,67 | 109,54 | =СУММ(C4:D4) |
| 5 | =СУММ(C3:C4) | =СУММ(D3:D4) | =СУММ(E3:E4) |
- Определим расчетное значение, введя формулу =(E5*(C3*D4-D3*C4)*(C3*D4-D3*C4))/(E3*E4*C5*D5) в ячейку Е7.
- Определим табличное значение критерия хи-квадрат, введя в ячейку Е8 вызов функции =ХИ2ОБР(0,05;1).
- Выполним сравнение расчетного и табличного значений. Поскольку расчетное значение (5,135995) больше критического (3,841455), то с уровнем значимости 0,05 нулевая гипотеза отклоняется. Следовательно, существует статистически значимая связь между курением и смертностью от указанных заболеваний.
Результаты работы приведены на рис. 4.21.

4.4.2. Таблицы вида 2´К
Таблица сопряженности типа 2´К имеет общий вид как табл. 4.20.
Для проверки нулевой гипотезы об однородности k выборок используется формула, предложенная Брандтом и Снедекором:
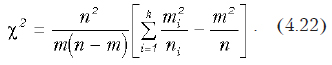
Расчетное значение сравнивается с критическим, взятым с (k-1) степенью свободы и заданным уровнем значимости. Если расчетное значение больше критического, то гипотезу об однородности следует отбросить и принять гипотезу о наличии между изучаемыми признаками существенной связи.
Таблица 4.20
Общий вид таблицы сопряженности вида 2´К
| № выборки или № уровня | Признак 1 | S | |||
| 2-го признака | Имеется | Отсутствует | |||
| 1 | m1 | n1 – m1 | n1 | ||
| 2 | m2 | n2 – m2 | n2 | ||
| .. | … | … | … | ||
| I | mi | ni – mi | ni | ||
| .. | … | … | … | ||
| k | mk | nk – mk | nk | ||
| S | m | n – m | N | ||
Пример
В примере, приведенном в 3.3.7, фактически выполняется анализ таблиц сопряженности данного вида. Отличие (чисто внешнее) в том, что табл. 4.20 является транспонированной по сравнению с табл. 3.19 (строки и столбцы менялись местами).
Для полноты картины данные, в которых представлена зависимость зараженности населения бруцеллезом типа Suis от частоты контактов с животными[4].
Таблица 4.21
Зараженность населения бруцеллезом типа Suis в зависимости от частоты контактов с животными
| Группа | Количество обследованных | ||
| обследованных | с положительной реакцией | с отрицательной реакцией | Всего |
| Работавшие в свинарнике | 19 | 42 | 61 |
| Имевшие эпизодические контакты с животными | 23 | 71 | 94 |
| Без контактов с животными | 23 | 227 | 250 |
| Итого | 65 | 340 | 405 |
Необходимо установить, имеется ли связь между уровнем зараженности бруцеллезом и степенью контактов населения с животными. В табл. 4.22 показано, как с помощью операций и функций Excel рассчитать предварительные данные, необходимые для расчета значения критерия c2.
Таблица 4.22
Подготовительные расчеты
| Строка / столбец | C | D | E | F |
| 3 | 19 | 42 | =СУММ(C3:D3) | =C3*C3/E3 |
| 4 | 23 | 71 | =СУММ(C4:D4) | =C4*C4/E4 |
| 5 | 23 | 227 | =СУММ(C5:D5) | =C5*C5/E5 |
| 6 | =СУММ(C3:C5) | =СУММ(D3:D5) | =СУММ(C6:D6) | =СУММ(F3:F5) |
После выполнения всех перечисленных действий мы имеем необходимую информацию для вычисления критериального значения. Для этого помещаем в ячейку Е8 формулу =E5*E5*(F6-C6*C6/E6)/(C6*(E6-C6)). Теперь необходимо получить критическое значение (процентную точку) распределения c2 для сравнения. В ячейку Е9 помещаем вызов функции =ХИ2ОБР(0,05;3-1). Здесь 0,05 — уровень значимости, а 3 — количество различных выборок. Поскольку 9,133466 > 5,991476, то нулевая гипотеза об отсутствии связи отклоняется. Таким образом, мы можем утверждать, что между степенью контактов населения с животными и заболеваемосью бруцеллезом существует статистически значимая связь.

4.4.3. Таблицы вида К´L
Таблицы вида К´L (см. табл. 4.2.1) являются наиболее общим видом таблиц сопряженности. В этом случае значениями признака 1 могут быть, например, различные виды лечения: симптоматическое, специфическое с нормальными дозами, специфическое с повышенными дозами или специфическое с добавлением других препаратов и пр. Значениями признака 2 могут быть, например, выздоровление за 2 недели, выздоровление за 4 недели, летальный исход.
Признак 2 может быть также совокупностью различных выборок. В этом случае применяется один критерий для проверки гипотез о независимости признаков и об однородности выборок. Для случая, когда первый столбец табл. 4.23 представляет собой К значения уровня второго признака, проверяется гипотеза о независимости первого и второго признаков. Если же первый столбец содержит k различных выборок, то проверяется гипотеза об однородности этих выборок (то есть, можно ли считать, что эти выборки извлечены из одной генеральной совокупности).
Значение критерия рассчитывается по формуле:
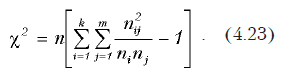
Расчетное значение сравнивается с критическим, взятым с (k–1)(m–1) степенями свободы и заданным уровнем значимости. Если расчетное значение больше критического, то гипотезу об однородности следует отбросить и принять гипотезу о наличии между изучаемыми признаками существенной связи.
Таблица 4.23
Общий вид таблицы сопряженности вида К´L
| Признак 2 | Признак 1 (m значений уровней) | Суммы | ||||||||
| (k значений уровней) | 1 | 2 | j | m | по строкам | |||||
| 1 | n11 | n12 | .. | n1j | … | n1m | n1 | |||
| 2 | n21 | n22 | … | n2j | … | n2m | n2 | |||
| … | … | … | … | … | … | … | … | |||
| i | ni1 | ni2 | … | nij | … | nim | ni | |||
| … | … | … | … | … | … | … | … | |||
| k | nk1 | nk2 | … | nkj | … | nkm | nk | |||
| Суммы по столбцам | n.k | n.2 | … | n.j | … | n.m | n..= n | |||
Пример
Рассмотрим задачу о распределении фракций ПВП (поливинилпирролидона в гемодезе различных производителей[5]. Исходные данные приведены в табл. 4.24.
Таблица 4.24
Распределении фракций ПВП (поливинилпиролидона в гемодезе различных производителей
| Производитель | Площадь пиков фракций ПВП | ||
| Препарата | высокомолекуляные с М,М>160000 | c номинальной М,М>8000+2000 | низкомолекулярные с М,М>4500 |
| АТ «Биохимик» | 15,4 | 80,1 | 4,5 |
| АТ «Биосинтез» | 16,7 | 78,3 | 4,8 |
| Днепропетровский ХФЗ | 31,9 | 65,1 | 2,5 |
| «Биолек» | 32,4 | 64,3 | 3,3 |
| АТ «Черкасымясо» з-д медпрепаратов | 20,7 | 77 | 2.4 |
| Пензенский з-д медпрепаратов | 37,9 | 58,4 | 3 |
| Несвижский з-д медпрепаратов | 29,6 | 67,8 | 2,4 |
Набираем приведенные выше данные в Excel (см. рис. 4.25). Для удобства при дальнейшем использовании таблица транспонирована (строки и столбцы поменялись местами). Сначала вычисляем суммы по строкам и столбцам, для чего набираем следующие вызовы функций.
Таблица 4.25
Подготовительные расчеты
| Номер ячейки | Содержание |
| L5 | =СУММ(L2:L4) |
| M5 | =СУММ(M2:M4) |
| N5 | =СУММ(N2:N4) |
| O5 | =СУММ(O2:O4) |
| P5 | =СУММ(P2:P4) |
| Q5 | =СУММ(Q2:Q4) |
| R5 | =СУММ(R2:R4) |
| S2 | =СУММ(L2:R2) |
| S3 | =СУММ(L3:R3) |
| S4 | =СУММ(L4:R4) |
| S5 | =СУММ(L5:R5) |

После этого формируем вспомогательную таблицу такого же размера как исходная.
Таблица 4.26
Формирование вспомогательной таблицы
| Cтолбец / Строка | 2 | 3 | 4 |
| T | =L2*L2/($L$5*$S2) | =L3*L3/($L$5*$S3) | =L4*L4/($L$5*$S4) |
| U | =M2*M2/($M$5*$S2) | =M3*M3/($M$5*$S3) | =M4*M4/($M$5*$S4) |
| V | =N2*N2/($N$5*$S2) | =N3*N3/($N$5*$S3) | =N4*N4/($N$5*$S4) |
| W | =O2*O2/($O$5*$S2) | =O3*O3/($O$5*$S3) | =O4*O4/($O$5*$S4) |
| X | =P2*P2/($P$5*$S2) | =P3*P3/($P$5*$S3) | =P4*P4/($P$5*$S4) |
| Y | =Q2*Q2/($Q$5*$S2) | =Q3*Q3/($Q$5*$S3) | =Q4*Q4/($Q$5*$S4) |
| Z | =R2*R2/($R$5*$S2) | =R3*R3/($R$5*$S3) | =R4*R4/($R$5*$S4) |
Не стоит пугаться — на самом деле набирается только формула =L2*L2/($L$5*$S2). Обратите внимание на размещение в формуле знаков $. Во все остальные ячейки формула размножается перетягиванием (см. раздел 1).
После этой предварительной работы можно получить расчетное значение для критерия c2. Для этого в ячейку W10 помещаем формулу =S5*(СУММ(T2:Z4)-1). Затем определяем критическое значение посредством вызова в ячейке W12 функции =ХИ2ОБР(0,05;(3-1)*(7-1)). Здесь 0,05 — уровень значимости, 3 и 7 — количество уровней варьирования (разных значений) первого и второго признаков. Поскольку расчетное значение (25,06148) больше критического (21,02606), то нулевая гипотеза отклоняется. Это значит, что по качеству препарата представленных производителей существуют статистически значимые различия. Результаты представлены на рис. 4.24.
4.4.4. Размер выборки и рандомизация
[Рандомизация] обеспечивает три вещи: она гарантирует, что наши наклонности и предпочтения не повлияют на формирование групп с различными обработками; она предотвращает опасность, связанную с выбором на основе личных суждений, — считая, что наши суждения могут быть пристрастными, мы стараемся учесть и устранить пристрастность и при этом можем перестараться, ударяясь в другую крайность; наконец, при случайном распределении обработок самый строгий критик не сможет сказать, что группы рассматривались по-разному вследствие наших предпочтений или нашей глупости.
А. Хилл [23]
Проблема рандомизации возникает когда данные, которые мы собираемся анализировать, получаются как некоторая выборка из генеральной совокупности. В этом случае возникает два вопроса:
- Сколько необходимо данных для принятия правильного решения?
- Как формировать выборку?
Количество данных, необходимых для анализа, зависит от следующих факторов:
- допустимой ошибки первого рода, то есть вероятности установить значимую зависимость, когда ее нет; обеспечивается за счет установки уровня значимости a;
- допустимой ошибки второго рода, то есть вероятности установить отсутствие связи, когда на самом деле она есть. Обычно задается через вероятность ошибки второго рода b или мощность критерия 1-b;
- от того, начиная с какой разницы частот мы будем считать их различие значимым.
Проблема в том, что уменьшение размера выборки ведет к уменьшению вероятности обнаружения значимого различия, а увеличение ее (выборки) — к увеличению вероятности признания значимыми несущественных различий.
Расчет размера выборки для случая подвыборок равных размеров
Сначала задаются уровень значимости a и мощность критерия 1-b. Затем необходимо установить частоты, которые мы будем считать различающимися. Обычно выбирается одна частота и устанавливается доля различия. После этого рассчитывается вторая частота по формуле
![]()
Здесь, Р1 — первая частота, а f — доля, с которой мы считаем различие значимым. Например, если Р1 = 0,6 и при этом f = 0,25 то P2 = 0,6 + 0,25(1-0,6) = 0,7. Это означает, что частоты 0,6 и 0,7 мы решили считать значимо различающимися.
Тогда размер каждой из двух подвыборок рассчитывается по формуле

При этом n — находится по формуле
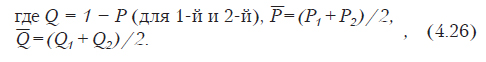
где Q = 1 – P (для 1-й и 2-й), , .
С помощью Excel эти формулы можно вычислить следующим образом. Допустим, что исходные данные находятся в следующих ячейках (см. табл. 4.27)
Таблица 4.27
Размещение исходных данных для расчета размера выборки при равных подвыборках
| Ячейка | Содержимое | Комментарий |
| А1 | 0,05 | a |
| В1 | 0,01 | b |
| С1 | 0,6 | P1 |
| D1 | 0,7 | P2 |
| B2 | =1-В1 | 1-b |
| C2 | =1-С1 | Q1 |
| D2 | =1- D1 | Q2 |
| C3 | =(С1+D1)/2 | |
| D3 | =(С2+D2)/2 |
Теперь можно рассчитать n` по формуле, которая помещена в ячейку C5:
=(НОРМСТОБР(A1/2)*КОРЕНЬ(2*C3*D3)-НОРМСТОБР(1-B1)*КОРЕНЬ(C1*D1-C2*D2))*(НОРМСТОБР(A1/2)*КОРЕНЬ(2*C3*D3)-НОРМСТОБР(1-B1) *КОРЕНЬ(C1*D1-C2*D2))/((D1-C1)*(D1-C1)).
После этого вычисляем размер выборки по формуле =ОКРВВЕРХ((C5/4)*(1+КОРЕНЬ(1+4/(C5*ABS(C1-D1))));1). В результате получаем значение размера выборки (359), удовлетворяющее поставленным условиям.
Расчет размера выборки для случая подвыборок разных размеров
Достаточно распространены ситуации, когда размеры выборок отличаются. В таком случае считаем, что размер одной выборки равен m, а второй N = (r + 1)m, где r в общем случае не равно 1. Тогда размер m вычисляется по формуле

где
а Q = 1 – P (для 1-й и 2-й), , как и в предыдущем случае.
С помощью Excel эти формулы можно вычислить следующим образом. Допустим, что исходные данные находятся в ячейках (см. табл. 4.26)
Таблица 4.26
Размещение исходных данных для расчета размера выборки при неравных подвыборках
| Ячейка | Содержимое | Комментарий |
| А1 | 0,05 | a |
| В1 | 0,01 | b |
| С1 | 0,6 | P1 |
| D1 | 0,7 | P2 |
| А2 | 2 | r |
| B2 | =1-В1 | 1-b |
| C2 | =1-С1 | Q1 |
| D2 | =1- D1 | Q2 |
| C3 | =(С1+D1)/2 | |
| D3 | =(С2+D2)/2 |
Теперь можно рассчитать m` по формуле, которая помещена в ячейку C5:
=(НОРМСТОБР(A1/2)*КОРЕНЬ((A2+1)*C3*D3)-НОРМСТОБР(1-B1)*КОРЕНЬ(A2*C1*D1-C2*D2))*(НОРМСТОБР(A1/2)*КОРЕНЬ(2*C3*D3)-НОРМСТОБР(1-B1) *КОРЕНЬ(C1*D1-C2*D2))/(A2*(D1-C1)*(D1-C1))
После этого вычисляем размер выборки по формуле =ОКРВВЕРХ((C5/4)*(1+КОРЕНЬ((2*(A2+1)/(1+A2*C5*ABS(C1-D1))));1).
После этого рассчитывается размер второй выборки по формуле =(А2+1)*В6. В В6 находится значение m.
Рандомизация
Если не делать рандомизацию, то выводы будут некорректны по причине с неслучайного формирования выборок вследствие нарушение исходных предпосылок случайности и независимости наблюдений. Осуществляется она следующим образом. Назначение пациентов в одну или другую группу выполняется с использованием таблиц случайных чисел [21]. Например, планируется подвергнуть испытанию 100 человек, 50 из которых назначают лекарственный препарат, а остальным плацебо. Для этого пациентам дают номера от 1 до 100. Затем выбирают 50 случайных чисел, равномерно распределенных в интервале 1..100. Пациентам, номера которых совпали с выбранными, назначают препарат, остальным — плацебо. Например, таблица 7.1а [1] содержит равномерно распределенные случайные числа. Если из этой таблицы взять ряд чисел 10, 09, 73, 25, 33, 76 и т.д. — это и будут необходимые нам номера.
Во многих случаях общее количество пациентов, которые будут подвергнуты испытанию может быть неизвестно (или таковых нет в наличии), а испытания проводят по мере поступления пациентов в клинику. В таком случае каждому новому поступившему назначают или препарат или плацебо. Для этого из таблицы случайных чисел выбирают последовательность, и если очередное число нечетное, то назначается препарат, если четное — плацебо. Например, если мы возьмем тот же ряд цифр 1, 0, 0, 9, 7, 3, 2, 5, 3, 3, 7, 6, то первому, четвертому, пятому, шестому, восьмому, девятому, десятому и одиннадцатому назначается препарат, а второму, третьему, седьмому и двенадцатому — плацебо. Более сложные ситуации с рандомизацией подробно изложены в [21].
Литература, рекомендуемая для изучения
- Большев Л.Н., Смирнов Н.В. Таблицы математической статистики.— 3-е изд.— М.: Наука, 1983.— 416 с.
- Браунли К.А. Статистическая теория и методология в науке и технике.— М.: Наука, — 407 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика. Учеб. пособие для втузов. — М.: Высш. Шк., 1977. — 479 с.
- Закс Л. Статистическое оценивание.— М.: Статистика, 1976. — 598 с.
- Кимбл Г. Как правильно пользоваться статистикой. — М.: Финансы и статистика, 1982. — 294 с.
- Кудрин А.Н., Пономарева Г.Т. Применение математики в экспериментальной и клинической медицине. — М.: Медицина, — 356 с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка — К.: ЗАO «Укрспецмонтажпроект», 1999. —312 с.
- Ликеш И., Ляга Й. Основные таблицы математической статистики.— М.: Финансы и статистика, 1985.— 356 с.
- Мисюк Н.С., Мастыркин А.С., Кузнецов Г.П. Корреляционно-регрессионный анализ в клинической медицине. — М.: Медицина, 1975. — 192 с.
- Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. — М.: Финансы и статистика, 1982.— 278 с.
- Плохинский Н.А. Алгоритмы биометрии. — М.: МГУ, 1980. — 150 с.
- Поллард Дж. Справочник по вычислительным методам статистики. — М.: Финансы и статистика, 1982. — 344 с.
- Рунион Р. Справочник по непараметрической статистике: Современный подход / Пер. с англ. Е.З. Демиденко; Предисл. Ю.Н. Тюрина. — М.: Финансы и статистика, 1982. — 198 с.
- Справочник по прикладной статистике. В 2 т. Т. 1: Пер. с англ. / Под ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина. — М.: Финансы и статистика, 1989. — 510 с.
- Справочник по прикладной статистике В 2 т. Т. 2: Пер. с англ.— М.: Финансы и статистика, 1990.— 526 с.
- Спрент П. Как обращаться с цифрами, или статистика в действии / Пер. с англ. А.Ф. Якубова.— Мн.: Выcш. шк., 1983.— 271 с.
- Терентьев П.В., Ростова Н.С. Практимум по биометрии. — Л.: ЛГУ, 1977. — 152 с.
- Тюрин Ю.Н. Непараметрические методы статистики.— М.: Знание, 1978.— 64 с.
- Тюрин Ю.Н. , Макаров А.А. Статистический анализ данных на компьютере. — М.: ИНФРА-М, 1998.— 528 с.
- Фёрстер Э., Рёнц Б. Методы корреляционного и регрессионного анализа. Руководство для экономистов / Пер. с нем. и предисл. В.М.Ивановой.— М.: Финансы и статистика, 1983.— 304 с.
- Флейс Дж. Статистические методы для изучения таблиц долей и пропорций.— М.: Финансы и статистика, 1989. — 319с.
- Хеттманспертер Т. Статистические выводы, основанные на рангах. — М.: Финансы и статистика, 1987. — 334 с.
- Хилл А. Основы медицинской статистики. — М.: Медгиз, 1958. — 306 с.
- Холлендер М., Вулф Д.А. Непараметрические методы статистики. — М.: Финансы и статистика, 1983.— 518 с.
[1] Адлер Ю.П., Маркова Е.В., Грановский Ю.В. Планирование эксперимента при поиске оптимальных условий.–М.: Наука, 1976.–280с.
[2] Данные для примера взяты из [9].
[3] Упорядоченном по величине.
[4] Дранкин Д.И., Заметин Б.А., Коржева В.С. // Микробиология. — 1960. — № 2.
[5] Сур С.В., Матюшова В.М., Нигматулин Р.Р. // Ліки України. — 1998. —.№ 3.