Гипотеза может быть проверена, но никогда не может быть доказана.
Л. Закс, «Статистическое оценивание»
Неизменно помни, что природа — не бог, человек — не машина, гипотеза — не факт.
Дени Дидро
3.1. Проверка статистических гипотез. Общие понятия
Статистические гипотезы — это гипотезы, которые относятся к виду или отдельным параметрам распределения случайной величины.
Опишем применяемую при этом терминологию.
Пусть f(X, q) — закон распределения случайной величины Х с некоторым параметром q. Тогда:
H0 (нулевая гипотеза) — q = q0,
H1 (альтернативная или конкурирующая гипотеза) — q = q1.
Нулевая гипотеза отклоняется в том случае, когда вероятность того, что она верна, оказывается ниже некоторого уровня, называемого уровнем значимости.
При анализе гипотез возможны ошибки двух видов:
- H0 отвергается, когда она верна.
- H0 принимается, когда верна H1.
Снижая уровень значимости мы уменьшаем вероятность ошибки первого рода, но при этом возрастает вероятность ошибки второго рода. Поэтому вводится понятие мощности критерия, которая представляет собой вероятность отклонения нулевой гипотезы. Поскольку эта вероятность изменяется при изменении параметров совокупности (например, размера выборки), то обычно рассматривают кривую мощности. На рис. 3.1 изображена кривая мощности для проверки биномиальной гипотезы р = 0,5.

На рисунке видно, что когда значение проверяемого параметра отклоняется от 0,5 в ту или иную сторону, вероятность совершить ошибку второго рода резко увеличивается.
Проверка гипотез обычно проходит следующие этапы.
- Определение используемой статистической модели. Здесь выдвигают некоторый набор предпосылок относительно закона распределения случайной величины и его параметров. Например, закон распределения нормальный, величины независимы и пр.
- Формулируют нулевую H0 и альтернативную H1 гипотезы.
- Выбирают критерий (критериальную статистику), который подходит к выдвинутой статистической модели.
- Выбирают уровень значимости a в зависимости от требуемой надежности выводов.
- Определяют критическую область для проверки нулевой гипотезы. Если значение критерия попадает в эту область, то нулевая гипотеза отклоняется. При условии, что гипотеза H0 верна, вероятность попадания в критическую область равна a. Вид этой области (односторонняя или двухсторонняя) зависит от принятой нулевой гипотезы.
- Рассчитывается значение выбранного статистического критерия для имеющихся данных.
- Рассчитанное значение критерия сравнивают с критическим (иногда называемым табличным) и затем решают: принять или отклонить нулевую гипотезу.
Односторонние и двусторонние критерии
В случае, когда нулевая гипотеза сформулирована в виде q = q0, используется двусторонний критерий.
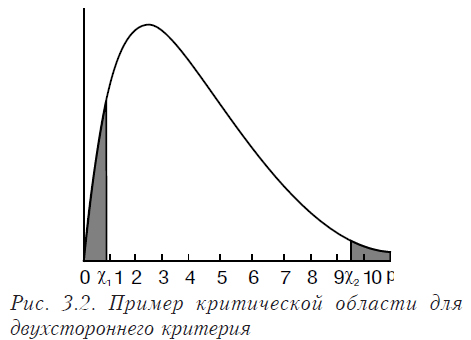
Если же мы формулируем нулевую гипотезу в виде q > q0 (или q < q0), то в этом случае используется односторонний критерий.
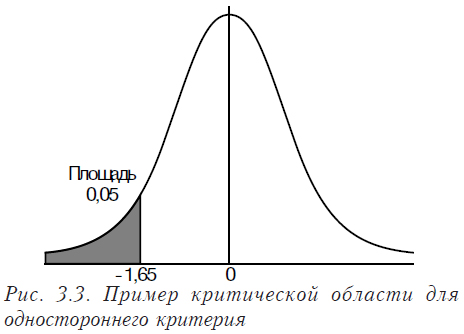
Устойчивость критериев
Любые гипотезы проверяют, выдвигая сначала комплекс некоторых предпосылок о законе распределения случайной величины. Невыполнение предпосылок делает выводы из соответствующих проверок не соответствующими истине. То есть вероятность неправильных выводов возрастает. Степень уменьшения надежности выводов у разных критериев отличается. Устойчивыми (робастными) называют такие критерии, для которых малые отклонения от принятых предпосылок (статистической модели) незначительно влияют на надежность выводов, сделанных по ним.
В связи с этим, при решении реальной задачи необходимо подобрать критерии, подходящие для условий именно этой задачи. Ввиду большого количества различных критериев (особенно непараметрических), это может вызвать некоторые затруднения у специалистов, для которых статистические методы являются всего лишь редко используемым инструментом. Поэтому мы предлагаем определенную последовательность действий, придерживаясь которой вы сможете сделать правильный выбор.
В данной книге рассматриваются не все известные критерии, а лишь наиболее часто используемые, для которых имеются средства обработки в распространенных программных средствах. Желающие познакомится с другими непараметрическими методами могут сделать это, обратившись к книгам Ю.Н. Тюрина [22], Дж. Полларда [15], Л. Закса [5], М. Холлендера [24].
3.1.1. Решаемые задачи
При выборе критерия необходимо всегда исходить из прикладной постановки задачи и природы данных.
Краткий путеводитель по статистическим методам проверки гипотез о положении и рассеивании позволяющий выбрать подходящий для вашей задачи, представлен в таблице 3.1.
Крайний левый столбец представляет собой формулировку задачи в прикладной области свою задачу вы должны свести к одной из этих формулировок. Если не получается, вернитесь в первый раздел и посмотрите общий перечень возможных задач.
Следующий столбец — формулировка этой задачи в терминологии, принятой в статистической литературе.
Столбец “Дополнительные условия” позволяет уточнить выбор метода в зависимости от особенностей ваших данных. Последний столбец — перечень методов, соответствующих определенному набору условий.
Например, ваша задача — сравнить две методики подготовки роженицы к родам. Сравнение эффективности выполняется по оценке состояния новорожденного, которая измеряется в баллах. В таблице — “Сравнение показателей контрольной и экспериментальной выборок”. Поскольку показатель измеряется в баллах, шкала является нечисловой (шкалой порядка). Для дальнейшего выбора необходимо оценить дисперсию. Для данной задачи ее обязательно нужно сравнивать (в контрольной и экспериментальной выборках). Это позволяет убедиться в том, что новая методика не дает большее рассеивание, чем старая. По таблице мы видим, что для этого необходимо применить метод Зигеля — Тьюки или Мозеса. Далее можно выбрать метод для проверки средних: Манна — Уитни (U-критерий Уилкоксона — Манна — Уитни) при равных дисперсиях и двухвыборочный Уилкоксона или медианный в противном случае.
Более подробно процедура выбора критерия рассматривается ниже.
Таблица 3.1
Выбор метода для решения задачи о сравнении параметров распределения выборок
| Формулировка задачи в прикладной постановке | Формулировка задачи в статистической постановке | Дополнительные условия |
Применяемый метод |
||
|
Сравнение показателей контрольной и экспериментальной выборок |
Проверка гипотезы о равенстве средних (центров распределения[1]) в двух независимых выборках |
Нормальный закон распределения Закон распределения отличный от нормального, или данные измеряются в нечисловой шкале[2] |
Дисперсии выборок равны
Дисперсии выборок не равны Без предположений о дисперсиях (но при одинаковом размере выборок) Дисперсии выборок равны Без предположений о дисперсиях |
t-критерий (Стьюдента) при равных дисперсиях
t-критерий (Стьюдента) при неравных дисперсиях t-критерий (Стьюдента) без предположений о дисперсиях Манна-Уитни (U-критерий Уилкоксона- Манна-Уитни) Двухвыборочный Уилкоксона, медианный |
|
| Сравнение показателей выборки до и после эксперимента | Проверка гипотезы о равенстве средних в двух зависимых выборках | Нормальный закон распределения
Закон распределения отличный от нормального или данные измеряются в нечисловой шкале |
t-критерий (Стьюдента) для связанных выборок
Знаковый, одновыборочный критерий Уилкоксона |
||
| Можно ли считать, что среднее значение показателя равно некоторому номинальному значению? | Проверка гипотезы о равенстве среднего константе | Нормальный закон распределения
Закон распределения отличный от нормального или данные измеряются в нечисловой шкале |
t-критерий (Стьюдента)
Гупта, знаковый |
||
| Сравнение рассеивания показателя в двух выборках | Проверка гипотезы о равенстве дисперсий (о принадлежности дисперсий к одной генеральной совокупности) | Нормальный закон распределения
Закон распределения отличный от нормального или данные измеряются в нечисловой шкале |
F-критерий (Фишера)
Зигеля-Тьюки, Мозэса |
||
| Можно ли считать, что в нескольких выборках имеет место одно и то же значение показателя? | Проверка гипотезы о равенстве дисперсий (о принадлежности дисперсий к одной генеральной совокупности) | Нормальный закон распределения
Закон распределения отличный от нормального или данные измеряются в нечисловой шкале |
G-критерий (Кохрена) при равном размере выборок, Бартлета
Фридмана |
||
| Можно ли считать, что в нескольких выборках имеет место одно и то же значение рассеивания показателя? | Проверка гипотезы о равенстве средних (о принадлежности средних к одной генеральной совокупности) | Нормальный закон распределения
Закон распределения отличный от нормального или данные измеряются в нечисловой шкале |
Шеффе, Диксона, дисперсионный анализ
Краскела-Уоллиса, медианный |
||
[1] В ряде случаев фактически проверяется гипотеза о равенстве медиан или же обоих мер положения
[2] О шкалах измерения смотри соответствующий раздел в предыдущей части
3.1.2. Последовательность операций при выборе критерия
Ниже приводится последовательность действий, придерживаясь которой вы подберете критерий, подходящий для решения вашей задачи.
- Сформулировать задачу. Возможные классы задач приведены ранее. В данной части мы рассматриваем задачи, связанные с проверкой каких-либо параметров закона распределения. Возможные виды прикладных задач приведены в таблице 2.1, а далее рассмотрены подробно.
- Определить класс применяемых критериев. Необходимо сделать выбор между параметрическими и непараметрическими критериями проверки гипотез.
- Определить дополнительные условия для выбора критерия. Многие критерии требуют выполнения дополнительных условий, без которых их использование будет некорректным.
- Выбор конкретного критерия. Для многих ситуаций существует несколько примерно равнозначных критериев, пригодных для проверки гипотезы.
Рассмотрим решение задачи выбора критерия более подробно.
Постановка задачи
Рассмотрим каждую возможную прикладную постановку задачи.
- Сравнение показателей контрольной и экспериментальной выборок. У нас есть две независимые выборки, средние значения некоторых параметров мы хотим сравнить. Например, две группы больных, лечение которых производится различными методами.
- Сравнение показателей выборки до и после эксперимента. В данном случае мы имеем дело с так называемыми связанными выборками. В литературе можно встретить также выражение “выборки, которые естественным образом разбиваются на пары”. Например, значение некоторого показателя в одной и той же группе больных до и после лечения.
- Можно ли считать, что среднее значение показателя равно некоторому номинальному значению? Для какого-то показателя (например, артериального давления, частоты пульса и пр.) может существовать некоторое значение, считающееся нормой. Нам необходимо проверить, можно ли считать, что среднее значение показателя в изучаемой группе равно норме. После проверки этой гипотезы для среднего доверительный обязательно следует построить интервал и проследить, чтобы для выборки выполнялись необходимые условия (см. 3.1.4).
- Сравнение рассеивания показателя в двух выборках. В некоторых биологических экспериментах важно не среднее значение показателя, а его рассеивание. Например, для последующей селекции новых сортов нам необходимо подобрать такой вид воздействия на семена, чтобы рассеивание признаков было наибольшим. Или же, необходимо выбрать препарат (метод лечения), для которых рассеивание контролируемого признака после применения будет минимальным.
- Можно ли считать, что в нескольких выборках имеет место одно и то же значение рассеивания показателя? Задача аналогична предыдущей, но сравниваются не два вида воздействия, а три и более.
- Можно ли считать, что в нескольких выборках имеет место одно и то же значение показателя? Например, мы применяем для лечения разных групп больных несколько препаратов-аналогов. Можем ли мы сказать, что результаты лечения статистически неотличимы?
Определение класса применяемых критериев
Необходимо осуществить выбор между параметрическими и непараметрическими критериями. Выбор зависит от закона распределения выборки и шкалы измерения, в которой представлены исходные данные.
Если данные измеряются в шкале наименований или шкале порядка (нечисловые шкалы), то применяются ранговые (непараметрические) критерии (подробнее шкалы описаны в соответствующем разделе). Напоминаем, когда значение качественное (есть/нет; пол; тяжесть заболевания; баллы, установленные экспертом и т.п.) мы имеем дело с нечисловой природой шкалы, хотя в таблице могут быть записаны числа (баллы, номер препарата и т.п.).
Ранговые (непараметрические) критерии применяются также и для числовых данных, в том случае, когда закон распределения выборки отличается от нормального.
Строгая проверка закона распределения требует большого количества данных, поэтому на практике обычно применяют упрощенные критерии. Рассмотрим один из них.
Можно считать, что случайная величина распределена по нормальному закону, если выполняются условия, являющиеся следствием из нормального закона распределения:
- Почти все (99,7%) отклонения от среднего меньше 3 сигм (ei < 3s).
- Две трети (68,3%) отклонений меньше, чем s.
- Половина отклонений меньше, чем 0,625s.
Если эти условия выполняются, можно считать, что гипотеза о нормальном распределении не противоречит имеющимся данным.
Все эти проверки основаны на свойствах нормального распределения (см. рис. 3.4).

Определение дополнительных условий для выбора критерия
Наиболее распространенными дополнительными условиями для выбора критерия являются:
- Равны или не равны размеры выборок?
- Равны или не равны дисперсии сравниваемых выборок?
- Одинаковы ли законы распределения сравниваемых выборок?
Последнее условие является требованием почти любого критерия, но никогда реально не подвергается проверке. Оно должно быть обеспечено правильным формированием выборок (см. 3.1.4).
Первое условие проверяется простым сравнением, а для проверки второго используются соответствующие критерии, которые выбираются аналогично.
Выбор конкретного критерия
Если есть несколько вариантов, критерий выбирается исходя из наличия программных средств или возможности проверки предпосылок для его использования.
3.1.3. Требования к выборкам
Наши выводы настолько достоверны, настолько хороши наши данные.
В.В. Швырков, «Тайна традиционной статистики Запада»
При проведении исследований (особенно клинических) необходимо обеспечить следующие свойства выборки.
Однородность. В выборке влияние изучаемой совокупности факторов на интересующие признаки не должно противоречить друг другу. Например, при исследовании влияния на организм человека кофе, в выборке испытуемых одновременно не должно быть людей, которых кофе возбуждает, и тех, которых от него клонит в сон[3]. В ряде случаев причины неоднородности могут быть неизвестны и поэтому перед анализом данных желательна проверка выборки методами кластерного анализа.
В выборке не должно быть значимо влияющих на исследуемый параметр факторов, кроме тех, которые мы изучаем. Если мы предполагаем, что фазы Луны влияют на эффективность действия препарата, то фазу Луны необходимо учитывать как фактор или учитывать влияние фактора, или собирать выборки, в которых фаза Луны одинакова)[4].
Репрезентативность (Структурное соответствие). Изучаемая выборка должна быть репрезентативна генеральной совокупности. Это означает, что когда мы формируем выборку из совокупности, она должна отвечать следующим требованиям:
- Вид статистического распределение выборки должен отвечать распределению генеральной совокупности.
- Величина выборки должна быть достаточна для отражения структуры генеральной совокупности.
В связи с этим понятно, что выборка, сформированная из больных, которые лечились в одной клинике или покупателей одной аптеки не является репрезентативной по своей структуре. Опрос, проведенный по телефону, отражает мнение только владельцев телефонов, а не всего населения, структура заболеваемости разных областей разная, маркетинговое исследование проведенное в Киеве нельзя распространить по своим выводам на города небольшого размера и т.д.
В тех случаях, когда мы сравниваем некоторые параметры двух выборок, необходимо обеспечить, равенство распределение частот влияющих факторов (пол, возраст, серьезность заболевания и пр.) в сравниваемых выборках.
Совпадение условий наблюдений. Условия наблюдения для отдельных элементов выборки или для двух сравниваемых выборок должны совпадать. Наилучшим способом обеспечения этого свойства является двойной слепой метод, при котором ни пациент, ни врач, ни средний медицинский персонал не знает какие лекарства или плацебо выдаются конкретному больному. Это позволяет избавиться от эффекта внушаемости (влияние которого возможно на 30 — 50 % пациентов) и эффекта предубежденности.
[3] Наиболее яркий пример — чувствительности людей к фенилтиокабамиду. Одни считают его очень горьким, другие же не чувствуют его вкуса вообще даже при большей в несколько тысяч раз концентрации (причем зависит это только от особенностей субъекта).
[4] Зависимость течения некоторых заболеваний от фаз Луны была научно доказана еще в начале ХХ века.
3.1.4. Примеры
Вечным законом да будет: учить и учится всему через примеры, наставления и применение на деле.
Ян Ямос Коменский
В предложенной задаче исследуется влияние антиагрегантной терапии на функциональную активность тромбоцитов при стабильной стенокардии. В качестве показателя используется тромбоцитарный тромбопластин. Измерение параметра выполняется в первый (столбец ФЗ_1) и пятый дни (столбец ФЗ_2) лечения (рис. 3.5). Необходимо выяснить, можем ли мы считать эффективным его действие на данный показатель. Из таблицы 3.1. следует, что это задача типа “Сравнение показателей выборки до и после эксперимента” для связанных выборок. Поскольку данные числовые, для выбора критерия необходимо принять или отвергнуть гипотезу о нормальном законе распределения выборок.
Решение задачи с использованием Microsoft Excel
Рассмотрим данный рисунок.

Столбцы С и D содержат по 10 значений показателя. Для проверки гипотезы о нормальном законе распределения сначала необходимо найти средние значения по каждой выборке. Для этого необходимо в ячейке С12 набрать следующий текст ”=AVERAGE(C2:C11)”, что обеспечит расчет среднего значения для столбца С. Аналогичные действия выполняются для второго столбца, только С заменяется на D (см. рис. 3.5.).
Затем необходимо вычислить среднеквадратичные отклонения для этих же выборок. Для этого в ячейку С13 (D13) следует записать функцию “=STDV(C2:C11)” (“=STDV(D2:D11)” для D13). Результат представлен на рис. 3.6.
Далее необходимо для каждого столбца рассчитать столбцы отклонений от среднего. На рис. 3.6. — F и G соответственно. Для этого в ячейках F2, F3 следует набрать формулы =C2-38,6 =C3-38,6 и т.д. (результат см. на рис. 3.6).
Теперь мы имеем всю информацию для проверки гипотезы о нормальном законе распределения.

Таблица 3.2
Проверка, является ли закон распределения нормальным
| Условие | Необходимо | 1-я выборка | 2-я выборка |
| Почти все (99,7 %) отклонения от среднего меньше 3 сигм (ei< 3s) | 10 | 10 | 10 |
| Две трети (68,3 %) отклонений меньше, чем s | 7 | 8 | 6 |
| Половина отклонений меньше, чем 0,625s | 5 | 4 | 5 |
Мы видим, что в каждой выборке одно из условий не выполняется (выделено), что не позволяет нам принять гипотезу о нормальном законе распределения. Это означает, что необходимо использовать непараметрические критерии. Допустим, никаких специальных программных средств мы не имеем. В таком случае выбираем знаковый критерий, как самый простой для реализации для связанных выборок.
Первое, что мы должны сделать — посчитать разницу между каждой парой элементов двух выборок. На рис. 3.7 это столбик С от 16 по 25 элемент. Для его расчета необходимо в каждую ячейку записать функцию расчета разницы. Например, в ячейку С16 “=С2-D2”. В остальных ячейках меняется только номер. Затем следует построить столбец знаков (“–” для отрицательной разницы, “+” для положительной и “0”, если разница равна нулю. Этот столбец можно построить “вручную” или с помощью функции, которая приведена на рис. 3.7 для ячейки D17.

Далее подсчитываем число положительных, нулевых и отрицательных разностей (1, 0 и 9 в нашем примере). Для дальнейшей работы необходимо выполнить следующие действия. В меню выбрать последовательно Insert, Macro, Module. У вас откроется лист Module. В этом листе необходимо набрать нижеприведенную функцию.
Option Base 1
‘Следующая функция, определенная пользователем,
‘возвращает вычисленное значение факториала.
Function FACT(NX) As Double
If NX < 0 Then ‘ Анализирует аргумент.
Exit Function ‘ Возврат в вызывающую
‘процедуру.
ElseIf NX = 0 Then
FACT = 1
Else
p = 1
For i = 1 To NX Step 1 ‘ Цикл выполняется NM раз.
p = p * i
Next i
FACT = p ‘ Возвращает вычисленное значение
‘ факториала.
End If
End Function
Function PROB_1(n, m, k, l) As Double
‘n — размер выборки
‘m — количество «-»
‘k — количество «+»
‘l — количество «0»
n = n — l
NM = n — m
p = 0
FN = FACT(n)
For i = 0 To NM Step 1 ‘ Цикл выполняется NM раз.
p = p + FN / (FACT(i) * FACT(n — i))
Next i
p = p / (2 ^ n)
PROB_1 = p
End Function
После этого в ячейке D29 набираем вызов этой функции (см. рис. 3.7.).

Результатом работы является число 0,01074. Это вероятность принять гипотезу о равенстве нулю медианы разности. Поскольку эта величина мала (меньше 0.05), то нулевую гипотезу мы отвергаем и считаем, что средние значения исследуемых выборок статистически значимо различаются.
Проверка данных на соответствие нормальному распределению
В предыдущем параграфе показан один из способов проверки, является ли закон распределения выборки нормальным. Поскольку описанный способ требует выполнения определенной последовательности действий и анализа вручную, а сама проверка — всего лишь вспомогательная операция, предлагаем вам набор функций, которые позволяют при их вызове получить ответ в виде надписи NORM или NO_NORM. Ниже приводится текст, который необходимо записать в рабочую книгу. Для чего необходимо в меню выбрать последовательно Insert, Macro, Module. Откроется лист Module, где и следует набирать текст:
Option Base 1 ‘ Помещается в самом начале модуля
‘Функция вычисления дисперсии выборки
Function VAR_1(R_1 As Object) As Double
‘Функция возвращает значение дисперсии выборки
‘R_1 — массив (анализируемая выборка)
Dim mas1() As Double
num_elem = R_1.Count ‘вычисление количества элементов в массиве
‘Инициализация временных переменных
Mean_Tmp = 0#
Var_Tmp = 0#
‘Вычисление среднего значения выборки
For i = 1 To num_elem
Mean_Tmp = Mean_Tmp + R_1.Cells(i)
Next i
Mean1 = Mean_Tmp / num_elem
‘Вычисление стандартного отклонения
For i = 1 To num_elem
Var_Tmp = Var_Tmp + (Mean1 — R_1.Cells(i)) ^ 2
Next i
‘Вычисление дисперсии выборки
VAR_1 = (Var_Tmp / (num_elem — 1))
End Function
Function STD_2(R_1 As Object) As Double
‘Функция возвращает значение стандартнго отклонения выборки
‘R_1 — массив (анализируемая выборка)
‘Вычисление среднеквадратического отклонения
STD_2 = VAR_1(R_1) ^ (1 / 2)
End Function
Function NORMSAMP_1(R_1 As Object) As String
‘R_1 — массив (анализируемая выборка)
num_elem = R_1.Count ‘вычисление количества элементов в массиве
Mean_Tmp = 0#
Abs_Tmp = 0#
‘Вычисление среднего
For i = 1 To num_elem
Mean_Tmp = Mean_Tmp + R_1.Cells(i)
Next i
Mean1 = Mean_Tmp / num_elem
‘Вычисление абсолютного среднего отклонения.
For i = 1 To num_elem
Abs_Tmp = Abs_Tmp + Abs(R_1.Cells(i) — Mean1)
Next i
Abs_1 = Abs_Tmp / num_elem
S_1 = STD_2(R_1)
x_1 = Abs(Abs_1 / S_1 — 0.7979)
y_1 = 0.4 / (num_elem ^ 1 / 2)
If x_1 < y_1 Then NORMSAMP_1 = «NORM»
If y_1 <= x_1 Then NORMSAMP_1 = «NO_NORM»
End Function
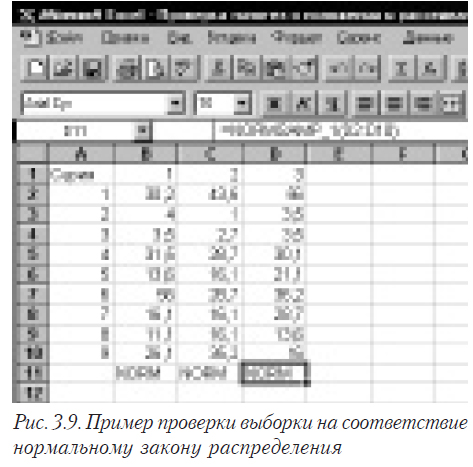
После этого вы можете в любом листе книги вызывать функцию NORMSAMP_1(), параметрами которой передаются интервалы ячеек, где находятся данные. Для примера предыдущего параграфа — NORMSAMP_1(C2:C11). Результатом будет появление в ячейке, в которой вызвана функция надписи NORM или NO NORM. На рис. 3.9. показан пример проверки, является ли закон распределения нормальным (столбец D — вызов функции, С — результат ее работы).
Замечания
Авторы просят обратить внимание на эти замечания, поскольку они обращены на типичные действия при проведении исследований.
- Достаточно обычной картиной для современных исследований является ситуация, когда имеется одна контрольная выборка и несколько экспериментальных (больше одной). Исследователь затем должен определить, какие из средних можно считать одинаковыми, а какие различными. Обычно это делают попарным сравнением средних. Это неправильно! Для таких действий необходимо использовать метод множественных сравнений Шеффе или его непараметрические аналоги.
- Очень часто, для того, чтобы в дальнейшем пользоваться критериями для нормального распределения, отбрасывают наибольшее и наименьшее значение. Действительно, получаемая после этого выборка, как правило, имеет нормальный закон распределения. Но, такое цензурирование выборки должно иметь под собой веские основания. Ведь вы фактически причисляете большие и малые значения к выбросам. В том случае, когда фактически это не выбросы, вы искажаете выборку, и соответственно будут искажены ваши выводы. Делать этого не нужно, ведь существует достаточно широкий спектр непараметрических методов, которые могут быть использованы в таких ситуациях.
3.2. Параметрические критерии проверки гипотез о средних и дисперсиях
Всякое исследование основано на сравнении и пользуется средством сопоставления.
Николай Кузанский
3.2.1. Критерий Фишера
Назначение. Проверка гипотезы о принадлежности двух дисперсий одной генеральной совокупности и следовательно — их равенстве.
Нулевая гипотеза. S12 = S22.
Альтернативная гипотеза. Существуют следующие варианты альтернативной гипотезы, в зависимости от которых различаются критические области:
- S12 > S22 Наиболее часто используемый вариант альтернативной гипотезы. Критическая область — верхний хвост F-распределения.
- S12 < S22 Критическая область — нижний хвост F-распределения. Ввиду частого отсутствия нижнего хвоста, в таблицах критическую область обычно сводят к варианту 1, меняя местами дисперсии.
- S12 ≠ S22 Двухсторонняя. Комбинация первых двух.
Предпосылки. Данные независимы и распределены по нормальному закону.
Краткие теоретические сведения. Гипотеза о равенстве дисперсий двух нормальных генеральных совокупностей принимается, если отношение большей дисперсии к меньшей меньше критического значения распределения Фишера.

где α — уровень значимости, v1 и v2 — степени свободы для дисперсии в числителе и знаменателе соответственно.
Примечание. При описываемом способе проверки значение Fрасч обязательно должно быть больше единицы. Критерий чувствителен к нарушению предположения о нормальности.
Пример
Приведены данные по двум независимым выборкам (см. таблицу 3.3) размера опухоли карциномы Герена на четвертый день заболевания. Было проведено исследование воздействия магнитными полями низкой частоты на новообразования.
Таблица 3.3
Результаты исследований
| Номер опыта | Номер выборки | |
| 1 | 2 | |
| 1 | 0,027 | 0,075 |
| 2 | 0,036 | 0,4 |
| 3 | 0,1 | 0,08 |
| 4 | 0,12 | 0,105 |
| 5 | 0,32 | 0,075 |
| 6 | 0,45 | 0,12 |
| 7 | 0,049 | 0,06 |
| 8 | 0,105 | 0,075 |
Прежде, чем мы будем проверять гипотезу о равенстве средних этих выборок, необходимо проверить гипотезу о равенстве дисперсий, чтобы знать какой из критериев выбрать для ее проверки.
На рис. 3.10 приведен пример проверки гипотезы о принадлежности двух дисперсий одной генеральной совокупности по критерию Фишера используя программный продукт Microsoft Excel.
Исходные данные размещены в ячейках, находящихся на пересечении столбцов C и D со строками 3–10. Выполним следующие действия.
- Определим, можно ли считать закон распределения первой и второй выборок нормальным (столбцы C и D соответственно). Если нет (хотя бы для одной выборки), то необходимо использовать непараметрический критерий (см. 3.1.5), если да — продолжаем.
- Рассчитаем дисперсии для первого и второго столбца. Для этого в ячейках C11 и D11 поместим функции =ДИСП(C3:C10) и =ДИСП(D3:D10) соответственно. Результатом работы этих функций является рассчитанное значение дисперсии для каждого столбца соответственно.
- Находим расчетное значение для критерия Фишера. Для этого нужно бóльшую дисперсию разделить на меньшую. В ячейку F13 помещаем формулу =C11/D11, которая и выполняет эту операцию.
- Определяем, можно ли принять гипотезу о равенстве дисперсий. Существует два способа, которые оба представлены в примере. По первому способу, задавшись уровнем значимости, например 0,05, вычисляют критическое значение распределения Фишера для этого значения и соответствующего числа степеней свободы. В ячейку F14 вводится функция =FРАСПОБР(0,05;7;7) (где 0,05 — заданный уровень значимости; 7 — число степеней свободы числителя, а 7 (второе) — число степеней свободы знаменателя). Число степеней свободы равно числу экспериментов минус единица. Результат — 3,787051. Поскольку это значение больше расчетного 1,601098, мы должны отвергнуть нулевую гипотезу о равенстве дисперсий и принять альтернативную — дисперсии не равны. По второму варианту рассчитывают для полученного расчетного значения критерия Фишера соответствующую вероятность. Для этого в ячейку F15 вводится функция =FРАСП(F13;7;7). Поскольку полученное значение 0,374835 больше, чем 0,05, то принимается гипотеза о различии дисперсий.

Это может быть выполнено специальной функцией. Выберите в меню последовательно пункты “Сервис”, “Анализ данных”. Появится окно следующего вида (рис. 3.11).
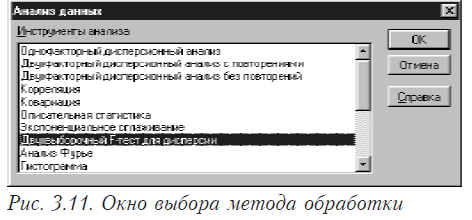
В этом окне выбираете “Двухвыборочный F-тест для дисперсий”. В результате появится окно вида, показанного на рис. 3.12 Здесь задаются интервалы (номера ячеек) первой и второй переменной, уровень значимости (альфа) и место, где будет находится результат.
Задавайте все необходимые параметры и нажимайте ОК. Результат работы приведен на рисунке 3.13.
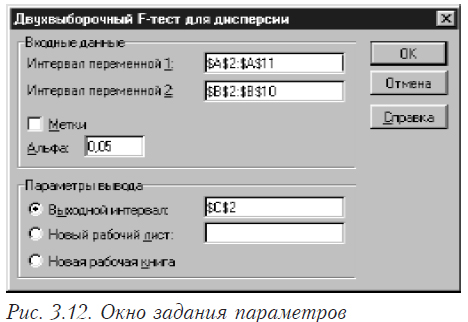

Следует отметить, что функция проверяет односторонний критерий и делает это правильно. Для случая, когда критериальное значение больше 1, вычисляется верхнее критическое значение. Когда критериальное значение меньше 1, то вычисляется нижнее критическое. Напоминаем, что гипотеза о равенстве дисперсий отвергается, если критериальное значение больше верхнего критического или меньше нижнего.
3.2.2. Анализ однородности дисперсий по Кохрену
Назначение. Проверка гипотезы о принадлежности нескольких дисперсий к одной генеральной совокупности.
Нулевая гипотеза.
Предпосылки.
Данные независимы и распределены по нормальному закону.
Краткие теоретические сведения. Критериальное значение рассчитывается по следующей формуле:

где S2max — максимальная из дисперсий; Si2 — эмпирические дисперсии, рассчитанные в каждой выборке.
Результат сравнивается с табличным. Если Gрасч < Gтабл, то гипотеза об однородности принимается.
Примечание
- Отклонение нулевой гипотезы может означать отличие закона распределения данных от нормального, а не неоднородность дисперсий.
Пример
При исследовании комбинированного действия верапамила, тетрадоксина и тетраэтиламония бромида на культуре тканей было проведено 9 экспериментов (по 3 раза каждый). Необходимо проверить, можно ли считать дисперсии во всех 9 экспериментах однородными. Если они таковыми не являются, это означает, что рассеяние зависит от доз каких-либо из изучаемых препаратов или имеются грубые ошибки в результатах наблюдений, связанные, например, с особенностями используемых в экспериментах животных, и пр. Результаты экспериментов приведены в таблице 3.4.
Таблица 3.4.
Результаты экспериментов
| Номер опыта | Угнетение синтеза белка (%) | ||
| Номер серии | |||
| 1 | 2 | 3 | |
| 1 | 30,2 | 43,6 | 56 |
| 2 | 4 | 1 | 3,5 |
| 3 | 3,5 | 2,7 | 3,5 |
| 4 | 31,5 | 28,7 | 30,1 |
| 5 | 13,6 | 16,1 | 21,1 |
| 6 | 56 | 28,7 | 36,2 |
| 7 | 16,1 | 16,1 | 28,7 |
| 8 | 11,1 | 16,1 | 13,6 |
| 9 | 26,1 | 35,2 | 16 |
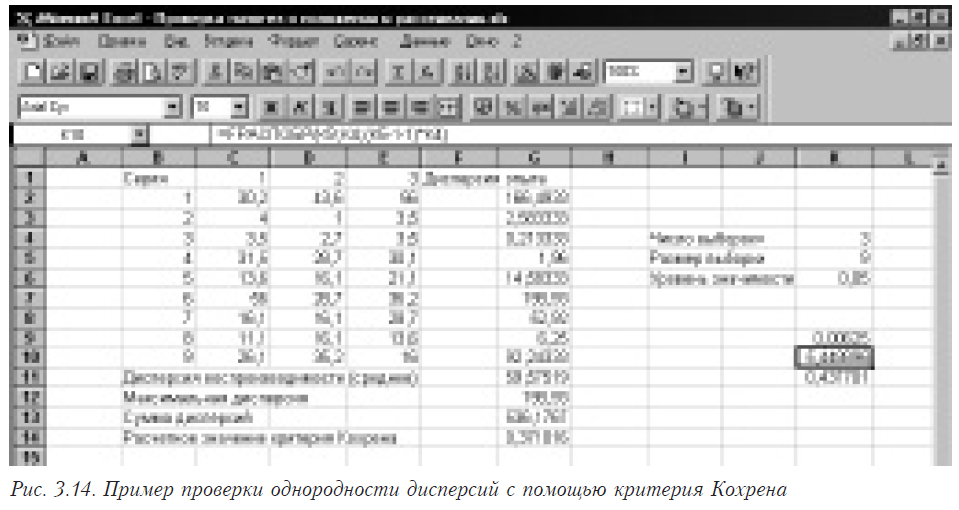
Рассмотрим решение этой задачи с помощью электронных таблиц Microsoft Excel. В столбиках C, D, E (строках 2–10) находятся исходные данные. Для выполнения анализа однородности по Кохрену необходимо выполнить следующие операции.
- Определить, можно ли считать закон распределения каждой выборки нормальным. Если нет (хотя бы для одной выборки), то следует использовать непараметрический (см. 3.1.5) критерий, если да — продолжать.
- В столбике G (строках 2–10) рассчитать дисперсии по каждому опыту. Для этого необходимо в ячейках G2–G 10 поместить функции расчета дисперсии: в G2 — =ДИСП(C2:E2), в G3 — =ДИСП(C3:E3) и т.д. Результатом будет столбик дисперсий по каждой строке.
- Найти максимальную из дисперсий. В ячейке G12 помещаем функцию =МАКС(G2:G10).
- Найти сумму дисперсий. В ячейке G13 помещаем функцию =СУММ(G2:G10).
- Найти расчетное значение критерия Кохрена для чего в ячейке G14 помещаем следующую формулу =G12/G13.
Таким образом, мы нашли расчетное значение критерия Кохрена — 0,379118. Теперь для проверки гипотезы его необходимо сравнить с табличным. Для этого надо получить значение соответствующей точки распределения Кохрена. Такой функции в Excel нет, но известно, что распределение Кохрена можно аппроксимировать распределением Фишера. При этом распределения связаны соотношением
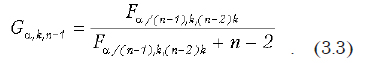
Для вычисления требуемого нам критического значения поместим в столбец К значения числа выборок (строка 4), размера выборки (строка 5), уровня значимости (строка 6). В строках 9–11 помещены формулы для расчета критической точки распределения:
К9 — =K6/(K5-1);
К10 — =FРАСПОБР(K9;K4;(K5-1-1)*K4);
К11 — =K10/(K10+K5-1-1).
В ячейке К11 и будет располагаться искомое значение критической точки распределения Стьюдента. В данном случае — 0,437701. Поскольку оно больше расчетного, то гипотеза об однородности в4ыборок принимается. Результаты работы приведены на рис.3.14.
3.2.3. Критерий Бартлета
Назначение. Проверка гиппотезы об однородности нескольких дисперсий. Применяется в случае, когда выборки, по которым определяются оценки дисперсий, имеют разный размер (в отличие от критерия Кохрена, требующего выборок равного размера).
Нулевая гипотеза. Изучаемые дисперсии принадлежат к одной генеральной совокупности: .
Альтернативная гипотеза. для конкретного i. То есть, хотя бы одна из дисперсий принадлежит другой генеральной совокупности.
Предпосылки. Распределение данных должно быть нормальным, данные независимы.
Краткие теоретические сведения
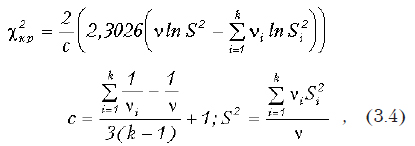
При этом — общее число степеней свободы; k — число групп; ni =ni–1 — число степеней свободы в каждой группе (ni – объем i-й группы); S2i — оценка дисперсии в каждой группе; S2 — взвешенная оценка дисперсии.
Если рассчитанное значение c2 больше или равно критическому значению, взятому с уровнем значимости a и числом степеней свободы n, то нулевая гипотеза принимается.
Примечание
- Данный критерий очень чувствителен к отклонению данных от нормального закона распределения. Если вы сомневаетесь в том, что исследуемые данные распределены в соответствии с нормальным законом распределения, данный критерий лучше НЕ ИСПОЛЬЗОВАТЬ.
Пример
Допустим, нам необходимо проверить однородность дисперсий независимых выборок данных, полученных в результате изучения влияния композиции МЕТАВИТ на процессы биотрансформации парацетамола при передозировке. При проведении экспериментов животные были разделены на 3 группы (табл. 3.5):
- интактные;
- те, которым вводили парацетамол + МЕТАВИТ;
- те, которым вводили парацетамол + МЕТИОНИН.
Таблица 3.5.
Результаты экспериментов
| Активность каталазы | ||
| Интактные | Парацетамол + МЕТАВИТ | Парацетамол + МЕТИОНИН |
| 97,81 | 103,63 | 99,34 |
| 169,59 | 126,4 | 103,59 |
| 111,5 | 147,98 | 114,12 |
| 148,27 | 121,82 | 112 |
| 158,22 | 110,01 | 84,6 |
| 133,08 | 87,5 | |
В данном случае, чтобы проверить однородность дисперсий по трем выборкам, сделаем следующее:
- Проверим имеющиеся у нас данные (по каждому столбцу отдельно) на соответствие их нормальному распределению. Эту проверку выполним при помощи функции NORMSAMP_1 (см. 3.1.5). Это необходимо сделать ОБЯЗАТЕЛЬНО, так как данный критерий очень чувствителен к отклонению анализируемых данных от нормального закона распределения.
- Вычислим для наших данных критериальное значение. Использовать формулу, приведенную выше, довольно сложно, поэтому предполагаем применить функцию BARTLET (), написанную на языке Visual Basic (полный текст данной функции приводится ниже). Ввод данной функции осуществляется согласно правилам, изложенным в подразделе 1.6. Общий вид таблицы и вводимой функции приведен на рис. 3.15. Необходимо отметить, что для использования данной функции анализируемые данные должны быть представлены в виде таблицы, столбцы которой следует расположить рядом, так как в функцию передается двумерный диапазон ячеек таблицы (на рис. 3.15 он показан в виде пунктирной линии). Для нашего примера рассчитанное критериальное значение будет равно 17,96099156.
Option Base 1 ‘ Помещается в самом начале модуля
‘Проверка гипотезы о равенстве нескольких дисперсий,
‘используя критерий Бартлета (анализируемые выборки могут
‘быть разного размера)
Function BARTLET(R_1 As Object) As Double
‘R_1 — двумерный массив ячеек
Dim i As Integer ‘вспомогательная переменная (счетчик)
Dim j As Integer ‘вспомогательная переменная (счетчик)
Num_row = R_1.Rows.Count ‘Вычисление количества строк
Num_col = R_1.Columns.Count ‘Вычисление количества столбцов
‘MsgBox «Количество строк» & Num_col
ReDim mas2(1 To Num_row, 1 To Num_col) ‘Рабочий массив
ReDim mas3(1 To Num_col) ‘Одномерный массив степеней свободы
ReDim mas_sigma(1 To Num_col) ‘Одномерный массив дисперсий
ReDim mas_mean(1 To Num_col) ‘Одномерный массив средних значений
v_all = 0# ‘Общее количество степеней свободы
‘Занесение содержимого ячеек электронной таблицы в рабочий
‘массив и попутное вычисление степеней свободы как каждой
‘выборки, так и общего числа степеней свободы
For j = 1 To Num_col ‘цикл по столбцам
mas3(j) = 0#
For i = 1 To Num_row ‘ цикл по строкам
mas2(i, j) = R_1.Cells(i, j)
‘ MsgBox «Value = » & R_1.Cells(i, j)
If mas2(i, j) <> «» Then mas3(j) = mas3(j) + 1
Next i
mas3(j)=mas3(j)-1 ‘Вычисление степени свободы j-го столбца
v_all = v_all + mas3(j) ‘Вычисление общей степени свободы
Next j
‘Инициализация вспомогательных переменных
c_val = 0#
c_temp = 0#
sigma_tmp = 0#
Mn_Tmp = 0#
‘Вычисление критериального значения
For j = 1 To Num_col ‘Цикл по столбцах
c_temp = c_temp + 1 / mas3(j)
Mn_Tmp = 0#
For i = 1 To mas3(j) + 1
Mn_Tmp = Mn_Tmp + mas2(i, j)
Next i
mas_mean(j) = Mn_Tmp / (mas3(j) + 1)
sigma_tmp = 0#
For i = 1 To mas3(j) + 1
sigma_tmp = sigma_tmp + (mas_mean(j) — mas2(i, j)) ^ 2
Next i
‘Вычисление оценки дисперсии в каждой группе
mas_sigma(j) = sigma_tmp / mas3(j)
Next j
c_val = (c_temp — 1 / v_all) / (3 * (Num_col — 1)) + 1
‘Вычисление взвешенной дисперсии sigma_all
sigma_all = 0#
sigma_tmp = 0#
var_tmp = 0#
For j = 1 To Num_col
sigma_tmp = sigma_tmp + mas3(j) * mas_sigma(j)
var_tmp = var_tmp + mas3(j) * Log(mas_sigma(j))
Next j
sigma_all = sigma_tmp / v_all
BARTLET=(2/c_val)*(2.3026*(v_all*Log(sigma_all)-var_tmp))
End Function

- Для того, чтобы принять или отвергнуть нулевую гипотезу, вычислим общее число степеней свободы. Это можно сделать как “вручную”, так и при помощи пользовательской функции BARTLET_DF () (текст см. ниже). Общее число степеней свободы для нашего примера — 14. Результат работы данной функции приведен на рис. 3.15.
‘Функция расчета общего числа степеней свободы, используемого
‘при проверке однородности дисперсий с помощью критерия Бартлета
Function BARTLET_DF(R_1 As Object) As Double
‘R_1 — двумерный массив ячеек
Dim i As Integer ‘вспомогательная переменная (счетчик)
Dim j As Integer ‘вспомогательная переменная (счетчик)
Dim v_temp As Integer ‘вспомогательная переменная (счетчик)
Num_row = R_1.Rows.Count ‘Вычисление количества строк
Num_col = R_1.Columns.Count ‘Вычисление количества столбцов
For j = 1 To Num_col ‘цикл по столбцам
v_temp = 0#
For i = 1 To Num_row ‘ цикл по строкам
If R_1.Cells(i, j) <> «» Then v_temp = v_temp + 1
Next i
v_temp = v_temp — 1 ‘Вычисление степени свободы j-го столбца
v_all = v_all + v_temp ‘Вычисление общего числа степеней свободы
Next j
BARTLET_DF = v_all
End Function
- Вычислим процентную точку распределения c2, используя встроенную статистическую функцию электронных таблиц ХИ2ОБР () и задавшись определенным уровнем значимости (для нашего случая возьмем 5% (0,05)). В данном примере (0,05;14) она будет равна 23,68478234. Так как это значение больше вычисленного на основании экспериментальных данных (17,96099156), то нулевую гипотезу о равенстве дисперсий мы вынуждены отвергнуть. На практике иногда предпочитают иметь дело не с процентными точками распределения c2, а с граничной вероятностью, которая соответствует вычисленному критериальному значению. Для вычисления граничной вероятности мы можем использовать встроенную функцию Microsoft Excel ХИ2РАСП (), аргументами которой являются рассчитанное критериальное значение (1-й аргумент) и общее число степеней свободы (2-й аргумент). На рис. 3.15 приведен результат работы данной функции. В нашем случае граничная вероятность Р(17,96099156; 14) равна 0,208563265. Это значение больше заданного нами уровня значимости (0,05), что позволяет отвергнуть гипотезу о равенстве дисперсий анализируемых выборок.
3.2.4. Проверка гипотезы о равенстве средних при неравных дисперсиях выборок
Назначение. Проверка равенства средних двух генеральных совокупностей, из которых извлечены две выборки.
Предпосылки.
Обе выборки извлечены из совокупности, имеющей нормальное распределение, данные независимы, дисперсии выборок различаются, выборки независимы.
Краткие теоретические сведения. Критериальное значение рассчитывается по формуле:
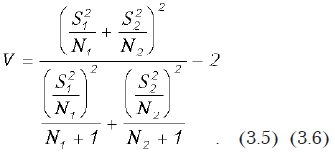
При этом
где N1 и N2 — размеры первой и второй выборок; и — эмпирические дисперсии; и — оценки средних значений; V — число степеней свободы для t-критерия. При вычислениях предполагается, что Х1 больше Х2.
Нулевая гипотеза
- H0 : = против H1 :¹ . В этом случае гипотеза о равенстве средних отвергается если по абсолютной величине критериальное значение больше верхней a/2 % точки t-распределения, взятого с V степенями свободы, то есть при .
- H0 : £ против H1 : > . Нулевая гипотеза отвергается, если критериальное значение больше верхней a% точки t-распределения, взятого с V степенями свободы, то есть при .
Примечание:
- Критерий устойчив при малых отклонениях от нормального распределения.
Пример
Рассматривается исследование эмбриотоксичности на лабораторных крысах (см. рис. 3.13). В ячейках C2:C11 — масса плода животных интактной группы, а в ячейках D2: D10 — животные, которым в полость желудка ежедневно вводили 0,6% масляный раствор 2-токоферола ацетата с 1 по 10 день беременности включительно в дозе 15мг/кг.
Сначала определим, можно ли считать закон распределения первой и второй выборок нормальным. Если нет (хотя бы для одной выборки), то необходимо использовать непараметрический критерий (см. 3.1.5), если да — продолжим.
Вычислим средние значения. Для этого в ячейку С12 (D12) помещаем функцию =СРЗНАЧ(C2:C11) (для D11 — =СРЗНАЧ(D2: D10). Затем вычисляем дисперсии этих выборок, для этого в ячейку С13 (D13) помещаем функцию =ДИСП(C2:C11) (для D13 — =ДИСП(D2: D10). Далее проверяем гипотезу о равенстве дисперсий, для чего рассчитывается значение критерия Фишера (с помощью формулы =C13/D13, помещенной в ячейку Е14). Затем определяется критическое значение вызовом в ячейке Е15 функции =FРАСПОБР(0,05;9;8). Здесь 0,05 — уровень значимости, а 9 и 8 — степени свободы дисперсий в числителе (10-1) и знаменателе (9-1) соответственно. Поскольку расчетное значение больше критического (4,27659 > 3,388124), то гипотеза о равенстве дисперсий отвергается в пользу гипотезы о том, что дисперсия первой выборки больше дисперсии второй.
Поскольку мы выяснили, что дисперсии выборок неравны, то для проверки гипотезы о равенстве средних как раз подходит этот критерий.
Осталось задать формулы для вычисления расчетного значения t-критерия и числа степеней свободы. Формула для вычисления расчетного значения t-критерия помещена в ячейку 17 и выглядит так: =(D12-C12)/КОРЕНЬ(C13/10+D13/9)). Здесь числа 10 и 9 — размеры первой и второй выборок. Мы получили значение 1,574214. Теперь необходимо рассчитать значение числа степеней свободы. В ячейке H7 мы помещаем соответствующую формулу:
=(C13/10+D13/9)*(C13/10+D13/9)/((C13/10)*(C13/10)/11+(D13/9)*(D13/9)/10)–2.
Здесь числа 11 и 10 — это увеличенные на единицу размеры выборок, а 10 и 9 — собственно размеры первой и второй выборок соответственно. В данном случае расчетное значение может быть дробным. Затем мы вычисляем критическое значение для распределения Стьюдента: в ячейку H9 помещаем вызов функции =СТЬЮДРАСПОБР(0,025;H7), где 0,025 — a/2 при 5% уровне значимости, H7 — адрес ячейки, в которой находится рассчитанное значение числа степеней свободы. Поскольку 1,574214 < 2,509569, гипотеза о равенстве средних принимается. Иллюстрирует пример рис.3.16.
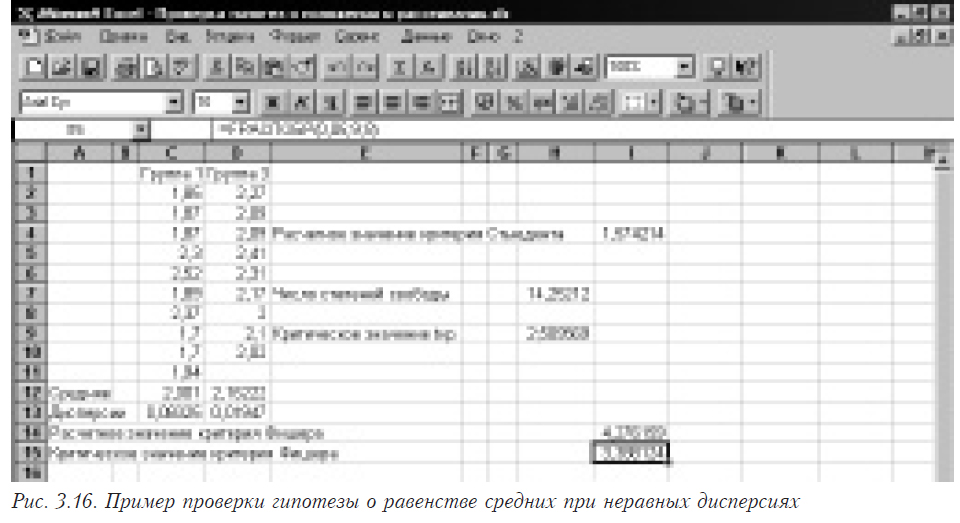
Рассмотрим, как решается такая задача непосредственно специальными средствами Excel. Предварительно нужно выяснить одинаковые дисперсии или нет. Допустим, они статистически значимо различаются. Выберите в меню последовательно пункты “Сервис”, “Анализ данных”. Появится окно следующего вида (рис. 3.17).

В этом окне выбираете “Двухвыборочный t-тест с различными дисперсиями”. В результате появится окно вида, показанного на рис. 3.18
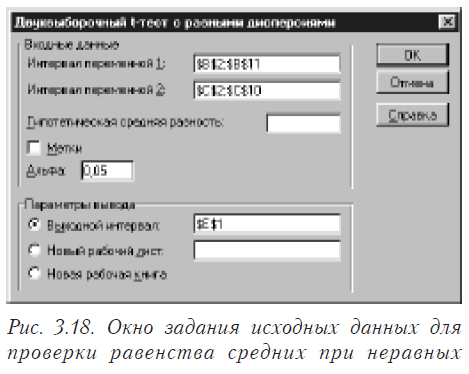
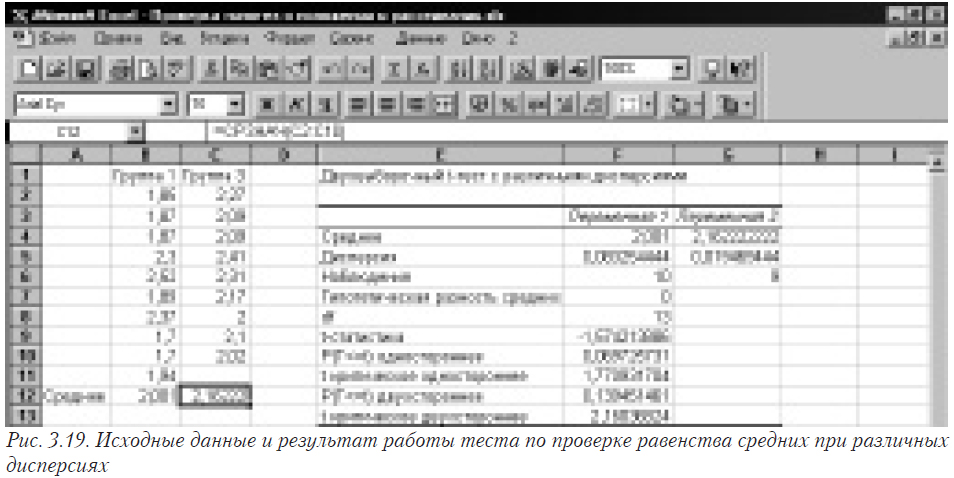
Здесь задаются интервалы (номера ячеек) первой и второй переменной, уровень значимости (альфа) и место, где будет находится результат. Результат работы приведен на рисунке 3.19 У вас теперь достаточно знаний, чтобы в нем разобраться. При задании “Гипотетической средней разницы” будет проверяться гипотеза, что разница средних значений равна указанной вами величине.
Как поступать при решении задач? Выбор на ваше усмотрение.
З.2.5. Проверка гипотезы о равенстве средних при равных дисперсиях
Назначение. Проверка равенства средних двух генеральных совокупностей, из которых извлечены две выборки.
Предпосылки
Обе выборки извлечены из совокупности, имеющей нормальное распределение.
Данные независимы.
Дисперсии выборок одинаковы.
Краткие теоретические сведения. Критериальное значение вычисляется по следующей формуле
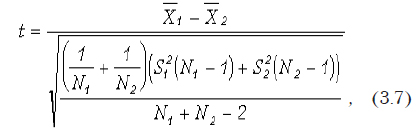
где N1 и N2 — размеры первой и второй выборок; и — эмпирические дисперсии; и — оценки средних значений.
Число степеней свободы для проверки t-критерия равно V = N1 + N2 — 2.
Нулевая гипотеза
- H0 : = против H1 :¹ . В этом случае гипотеза о равенстве средних отвергается, если по абсолютной величине критериальное значение больше верхней a/2 % точки t-распределения, взятого с V степенями свободы, то есть при .
- H0 : £ против H1 :> . Нулевая гипотеза отвергается, если критериальное значение больше верхней a% точки t-распределения, взятого с V степенями свободы, то есть при .
Примечание
- Критерий устойчив при малых отклонениях от нормального распределения.
- При невыполнении условия равенства дисперсий критерий устойчив только для случая выборок равного объема.
Пример
Сначала определим, можно ли считать закон распределения первой и второй выборок нормальным. Если нет (хотя бы для одной выборки), используем непараметрический критерий (см. 3.1.5), если да — продолжаем. После этого определяем, равны ли дисперсии этих выборок.
Используем данные, приведенные в разделе 3.6.1. Поскольку мы выяснили, что дисперсии выборок равны, то нам нужен именно этот критерий. Для дальнейшей работы, кроме дисперсий (см. пример в 3.2.1) необходимо еще вычислить и средние значения. Для этого в ячейки С12 (D12) помещаем функцию =СРЗНАЧ(C3:C10) в С12 и =СРЗНАЧ(D3:D10) в D12. Затем рассчитываем число степеней свободы в ячейке I4 (=ЧСТРОК(C3:C10)+ЧСТРОК(D3:D10)-2), после чего вычисляем критериальное значение по формуле в Н7=(C12-D12)/КОРЕНЬ(((1/8)+(1/8))*(C11*7+D11*7)/H7). Здесь 8 — размеры выборок (в данном примере одинаковы), Н7 — адрес ячейки, в которой находится значение числа степеней свободы. Получено значение 0,394888. В этой ситуации дальнейшую проверку проводить не стоит, поскольку любое критериальное значение больше 1, а следовательно больше полученного числа — гипотеза о равенстве средних принимается. Но для того, чтобы показать последовательность действий в обычной ситуации, продолжим вычисления. Остается рассчитать критическое значение распределения Стьюдента с помощью формулы в ячейке Н9=СТЬЮДРАСПОБР(0,025;H7). Здесь 0,025 — a/2 при 5% уровне значимости, H7 — адрес ячейки, в которой находится рассчитанное значение числа степеней свободы. Пример показан на рис. 3.20.
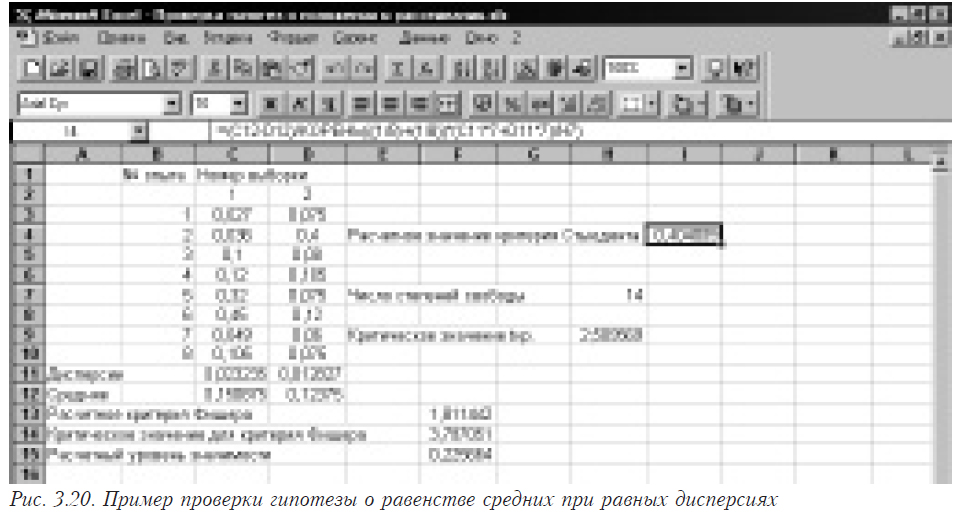
Рассмотрим, как решается такая задача непосредственно специальными средствами Excel. Предварительно нужно выяснить одинаковые дисперсии или нет. Допустим, они не различаются статистически значимо. Выберите в меню последовательно пункты “Сервис”, “Анализ данных”. Появится окно следующего вида (рис. 3.17). В этом окне выбираете “Двухвыборочный t-тест с одинаковыми дисперсиями”. В результате появится окно вида, показанного на рис. 3.21.
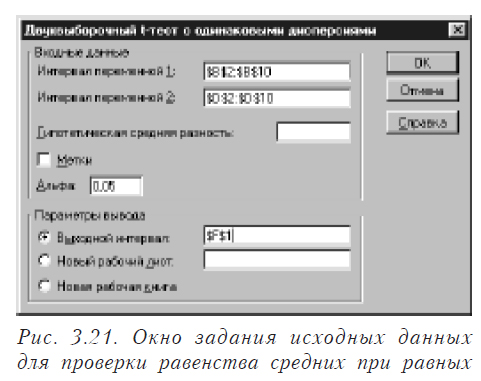
В этом окне задаем исходные данные для обработки и нажимаем ОК. Результаты работы приведены на рисунке 3.22. При задании “Гипотетической средней разницы” будет проверяться гипотеза, что разница средних значений равна указанной вами величине.
Надеемся, что вы можете в них разобраться и сделать соответствующие выводы, поскольку все необходимые для этого знания вами уже получены.

3.2.6. Проверка гипотезы о равенстве средних без предположений о дисперсиях
Назначение. Проверка равенства средних двух генеральных совокупностей, из которых извлечены две выборки.
Предпосылки.
Обе выборки извлечены из совокупности, имеющей нормальное распределение.
Данные независимы.
Размеры выборок одинаковы, выборки независимы.
Краткие теоретические сведения. Критериальное значение вычисляется по формуле
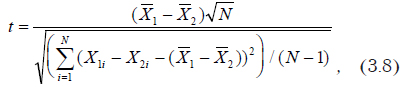
где N — размер первой и второй выборок; и — оценки средних значений; и — текущие значения переменных.
Число степеней свободы для t-критерия V = N — 1.
Нулевая гипотеза
- H0 : = против H1 :¹ . В этом случае гипотеза о равенстве средних отвергается если по абсолютной величине критериальное значение больше верхней a/2 % точки t-распределения, взятого с V степенями свободы, т.е при .
Примечание
- Критерий устойчив при малых отклонениях от нормального распределения.
Пример
Допустим, нам необходимо выяснить, различается ли статистически значимо влияние лечения различными антикоагулянтами на фибринолиз. У нас есть 2 выборки (столбцы) независимых данных, полученных в результате медико-биологических исследований (табл. 3.6). Для того, чтобы сделать научно обоснованные выводы, нам необходимо проверить гипотезу о равенстве средних, не делая предположений о дисперсиях.
Таблица 3.6
Результаты влияния лечения различными антикоагулянтами на фибринолиз
| Лечение 1-м антикоагулянтом | Лечение 2-м антикоагулянтом |
| 5,6 | 3,6 |
| 5,9 | 4 |
| 4,9 | 5,2 |
| 5,9 | 4 |
| 6,6 | 4,4 |
| 4,5 | 4,7 |
| 3,1 | 5,9 |
| 3,9 | 3,4 |
| 4,9 | 4 |
| 5,7 | 5,5 |
| 4,9 | 5 |
| 5,7 | 4,2 |
- Проверим имеющиеся у нас данные на соответствие их нормальному распределению по столбцам. Выполним это при помощи функции NORMSAMP_1 () (см. 3.1.5). Данная функция, не является встроенной в Microsoft Excel и, поэтому, ее текст необходимо ввести согласно правилам, описанным в 1.6.
- Основываясь на имеющихся данных, вычислим критериальное значение. Использование вышеприведенной формулы затруднительно из-за ее сложности, поэтому лучше использовать функцию T_CRIT3 (), написанную на языке Visual Basic. Входными данными данной функции являются два массива ячеек. В нашем примере вызов функции осуществляется следующим образом: =T_CRIT3(B3:B14;C3:C14), где B3:B14 — первая выборка и C3:C14 — вторая. Полный текст функции T_CRIT3 () приведен далее, ее ввод осуществляется согласно правилам, описанным в 1.6. Общий вид электронной таблицы и вводимой функции приведен на рис. 3.15. Для нашего примера рассчитанное критериальное значение будет равно 1,5559525, а число степеней свободы — 11.
Option Base 1 ‘ Помещается в самом начале модуля
Function T_CRIT3(R_1 As Object, R_2 As Object) As Double
‘Вычисление критериального значения при проверке равенства
‘средних двух генеральных совокупностей независимых выборок
‘без предположений о дисперсиях
‘R_1 — 1-й массив (1-я анализируемая выборка)
‘R_2 — 2-й массив (2-я анализируемая выборка)
N_el = R_1.Count ‘вычисление количества элементов в выборке
sum_1 = 0#
sum_2 = 0#
sum_3 = 0#
AMean_1 = 0#
AMean_2 = 0#
AMean_dif = 0#
‘вычисление средних значений анализируемых выборок
For i = 1 To N_el
sum_1 = sum_1 + R_1.Cells(i)
sum_2 = sum_2 + R_2.Cells(i)
Next i
AMean_1 = sum_1 / N_el
AMean_2 = sum_2 / N_el
AMean_dif = Abs(AMean_1 — AMean_2)
For i = 1 To N_el
sum_3=sum_3+(R_1.Cells(i)-R_2.Cells(i)-(AMean_1 — AMean_2))^2
Next i
T_CRIT3 = (AMean_dif * Sqr(N_el)) / Sqr(sum_3 / (N_el — 1))
End Function
- Для того, чтобы сделать вывод относительно равности средних исследуемых выборок, мы можем воспользоваться таблицами распределения Стьюдента. Однако, имея такое мощное программное средство как Microsoft Excel мы можем обойтись без таблиц и использовать встроенные функции для вычисления как граничной вероятности СТЬЮДРАСП () (для нашего примера необходимо ввести =СТЬЮДРАСП(B16;B17;2)), так и процентной точки распределения Стьюдента при помощи функции СТЬЮДРАСПОБР() (для нашего примера необходимо ввести =СТЬЮДРАСПОБР(0,025;B17)). При вводе функции =СТЬЮДРАСП(B16;B17;2) следует помнить, что третий аргумент должен быть равен 2, так как нам необходимо двустороннее распределение. Основываясь на полученных результатах можно сделать вывод о том, что средние анализируемых выборок равны, так как рассчитанное критериальное значение (1,5559525) меньше табличного (2,593096724) при уровне значимости 0,05 и числе степеней свободы 11. Аналогичный вывод можно сделать, основываясь на рассчитанной граничной вероятности (0,148003955). Пример см. на рис. 3.23.
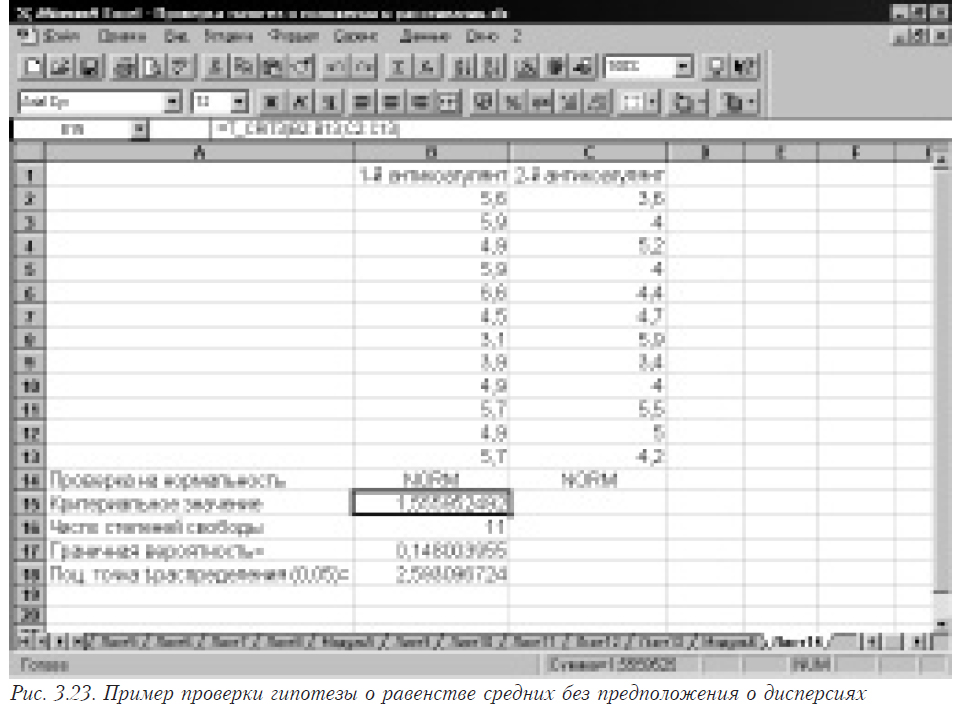
3.2.7. Проверка гипотезы о равенстве среднего заданному значению А
Назначение. Проверка равенства среднего определенному значению.
Предпосылки. Выборки извлечена из совокупности, имеющей нормальное распределение, данные независимы.
Краткие теоретические сведения. Критериальное значение вычисляется по формуле

где N — размер выборки; S2 — эмпирическая дисперсия выборки; A — предполагаемая величина среднего значения; — среднее значение.
Число степеней свободы для t-критерия V = N — 1.
Нулевая гипотеза
- H0 : = А против H1 : А. Нулевая гипотеза о равенстве средних отвергается если по абсолютной величине критериальное значение больше верхней a/2 % точки t-распределения взятого с V степенями свободы, то есть при .
- H0 : А против H1 : > А. Нулевая гипотеза отвергается, если критериальное значение больше верхней a% точки t-распределения взятого с V степенями свободы, то есть при .
- H0 : А против H1 : < А. Нулевая гипотеза отвергается, если критериальное значение меньше нижней a% точки t-распределения, взятого с V степенями свободы,.
Примечание
- Критерий устойчив при малых отклонениях от нормального распределения.
Пример.
Рассмотрим пример, представленный на рис. 3.24. Допустим, что нам необходимо проверить гипотезу о равенстве среднего для выборки (ячейки I23I30) величине 0,012.
Сначала находим среднее выборки (=СРЗНАЧ(I23:I30) в I31) и дисперсию (=ДИСП(I23:I30) в I32). После этого рассчитываем критериальное (=(I31-0,012)*КОРЕНЬ(I33)/I32) и критическое (=СТЬЮДРАСПОБР(0,025;I33-1)) значения. Поскольку критериальное значение (24,64) больше критического (2,84), то гипотеза о равенстве среднего 0,012 отвергается.

3.2.8. Проверка гипотезы о равенстве средних
при связанных выборках
Назначение. Проверка равенства средних двух генеральных совокупностей, из которых извлечены две выборки, при условии, что выборки связанные. Например, значения каких-то параметров до и после лечения, в процессе старения организма и т.п. Хотя для этих целей используют обычный критерий (приведенный выше), рекомендуют пользоваться специальным критерием.
Предпосылки. Обе выборки извлечены из совокупности, имеющей нормальное распределение.
Данные независимы.
Выборки связанные.
Краткие теоретические сведения. Критериальное значение вычисляется по формуле:
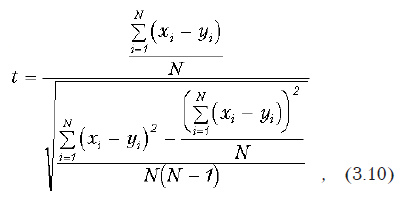
где xi и yi — значения связанных рядов наблюдений; N — величина выборки (каждой, так как они одинаковы).
Число степеней свободы для t-критерия V = N — 1.
Нулевая гипотеза
- H0 : = против H1 :¹ . В этом случае гипотеза о равенстве средних отвергается, если по абсолютной величине критериальное значение больше верхней a/2 % точки t-распределения, взятого с V степенями свободы, то есть при .
- H0 : £ против H1 :> . Нулевая гипотеза отвергается, если критериальное значение больше верхней a% точки t-распределения взятого с V степенями свободы, т.е при .
- H0 : ³ против H1 :< Нулевая гипотеза отвергается, если критериальное значение меньше нижней a% точки t-распределения, взятого с V степенями свободы,.
Примечание:
- Положительной стороной этого критерия является то, что даже при значительных отклонениях переменных xi и yi от нормального закона их разность будет достаточно точно распределена по нормальному закону.
Пример
Рассмотрим пример, в котором необходимо выяснить, оказала ли антиагрегантная терапия значимое влияние на функциональную активность тромбоцитов. Данные, полученные в результате исследования, приведены в таблице 3.7. Для достижения нашей цели выполним следующие действия.
Таблица 3.7 Данные результатов исследований
| Больные | Тромбоцитарный фибриноген | |
| до лечения | после лечения | |
| 1 | 1 | 0,9 |
| 2 | 1,3 | 1,3 |
| 3 | 1,4 | 1 |
| 4 | 0,9 | 0,8 |
| 5 | 0,7 | 1,1 |
| 6 | 1,8 | 1,6 |
| 7 | 1,1 | 0,9 |
| 8 | 1,2 | 0,9 |
| 9 | 0,6 | 0,6 |
| 10 | 0,5 | 0,6 |
- Проверим имеющиеся у нас данные на соответствие их нормальному распределению по столбцам. Выполним это при помощи функции NORMSAMP_1 () (см. 3.1.5). Данная функция, не является встроенной в Microsoft Excel, поэтому ее текст необходимо ввести согласно правилам, описанным в подразделе 1.6.
- Вычислим критериальное значение (см. рис. 3.24). Так как вышеприведенная формула сложна для прямого применения, мы предлагаем использовать функцию T_CRIT2 (), написанную на языке Visual Basic. Входными данными этой функции являются два массива ячеек (два столбца, один из которых содержит значения исследуемого показателя до лечения, другой — после лечения). В нашем примере вызов функции осуществляется следующим образом: =T_CRIT2(C4:C13;D4:D13), где C4:C13 — первая выборка (до лечения) и D4:D13 — вторая (после лечения). Полный текст функции T_CRIT2 () приведен далее. Ввод осуществляется согласно правилам, описанным в 1.6. Для нашего примера рассчитанное критериальное значение будет равно 3,857142857, а число степеней свободы — 9.
Option Base 1 ‘ Помещается в самом начале модуля
Function T_CRIT2(R_1 As Object, R_2 As Object) As Double
‘Вычисление критериального значения при проверке равенства
‘средних двух генеральных совокупностей связанных выборок
‘R_1 — 1-й массив (1-я анализируемая выборка)
‘R_2 — 2-й массив (2-я анализируемая выборка)
N_el = R_1.Count ‘вычисление количества элементов в массиве
sum_1 = 0#
sum_2 = 0#
For i = 1 To N_el
sum_1 = sum_1 + Abs(R_1.Cells(i) — R_2.Cells(i))
sum_2 = sum_2 + (R_1.Cells(i) — R_2.Cells(i)) ^ 2
Next i
T_CRIT2=(sum_1/N_el)/((sum_2-(sum_1^2)/N_el)/(N_el*(N_el-1)))^(1/2)
End Function
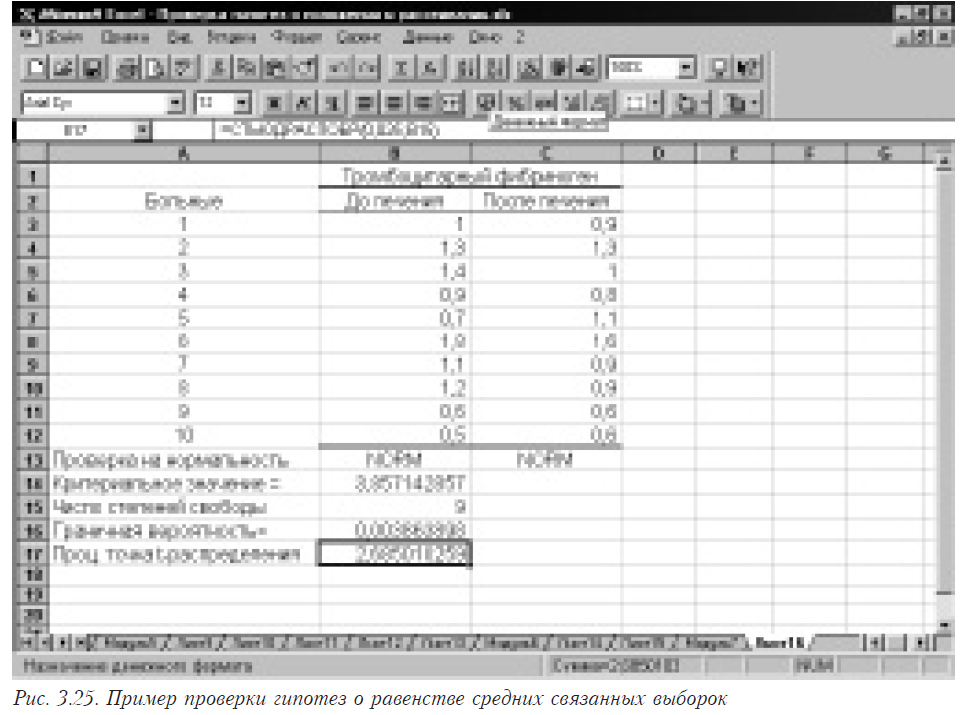
- Для того, чтобы сделать вывод относительно равенства средних двух связанных выборок мы воспользуемся встроенными функциями Microsoft Excel для вычисления как граничной вероятности СТЬЮДРАСП () (для нашего примера необходимо ввести =СТЬЮДРАСП(C15; C16; 2)), так и процентной точки распределения Стьюдента при помощи функции СТЬЮДРАСПОБР() (для нашего примера необходимо ввести =СТЬЮДРАСПОБР(0,025; C16)). При вводе функции =СТЬЮДРАСП(C15;C16;2)) следует помнить, что третий аргумент должен быть равен 2, так как нам необходимо двустороннее распределение, а при вводе =СТЬЮДРАСПОБР(0,025; C16)) значение первого аргумента возьмем равным 0,025 (если a = 0,05, то a/2 = 0,025). Основываясь на полученных результатах, приходим к выводу, что средние анализируемых связанных выборок не равны, так как рассчитанное критериальное значение (3,857142857) больше табличного (2,685010259) при уровне значимости a/2 = 0,025 и числе степеней свободы 9. Аналогичный вывод можно сделать, основываясь на рассчитанной граничной вероятности (0,003863898). Полученные результаты следует интерпретировать таким образом, что антиагрегантная терапия значимо влияет на один из параметров функциональной активности тромбоцитов (тромбоцитарный фибриноген).
О возможных парадоксах при проверке гипотез о средних
При проверке гипотез вполне возможны следующие ситуации:
- Подтверждены гипотезы=и =, но отвергнута¹.
- Подтверждены гипотезы =А и =А, но отвергнута ¹.
В связи с этим, для проверки равенства нескольких средних необходимо пользоваться специальными критериями.
Некоторые замечание к проверкам средних
- Следует помнить, что в том случае, когда выборка формируется неслучайным способом, стандартные отклонения уменьшаются, а разница средних значений увеличивается.
- Возможно сравнение параметров на основании сопоставления их доверительных интервалов. При этом, если интервалы не перекрываются, то между параметрами имеется статистически значимая разница. Если же доверительные параметры перекрываются частично, то из этого не следует, что они отличаются незначимо.
Определение размера выборки
Для определение минимального объема выборки, необходимого для оценки значения исследуемого параметра можно воспользоваться следующей формулой.
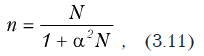
где n — искомый размер выборки; N — размер генеральной совокупности; a — уровень значимости при проверки гипотезе о значении параметра.
- Проверка равенства нескольких средних посредством дисперсионного анализа
Назначение. Проверка гипотезы о принадлежности нескольких средних значений к одной генеральной совокупности.
Нулевая гипотеза.
Предпосылки.
Распределение данных должно быть нормальным.
Данные независимы.
Краткие теоретические сведения. Используется методология дисперсионного анализа (см. 4.2). Рассчитывается критериальное значение
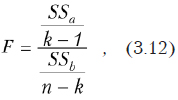
где — общее количество экспериментов; ni — объем i-ой выборки; — сумма квадратов межвыборочного рассеивания ( — среднее значение по i-ой выборке, а — общее среднее значение по объединенной выборке); внутривыборочная сумма квадратов, где — значение переменной в j-м эксперименте i-ой выборки.
Если рассчитанное критериальное значение больше критического значения распределения Фишера, взятого с некоторым уровнем значимости и степенями свободы (k-1) и (n-k), то нулевая гипотеза отвергается. То есть средние значения (по крайней мере, некоторые из них) принадлежат разным генеральным совокупностям и являются различными.
- Метод множественных сравнений Шеффе
Довольно частой является ситуации, когда необходимо сравнить между собой не два значения средних, а несколько. Сравнение с помощью дисперсионного анализа (см. параграф 3.2.9) позволяет выяснить, можем ли мы считать их равными или нет. В случае, когда они не равны, представляет интерес выяснение вопроса, какие средние значения равны между собой, а какие отличаются, а также какие группы средних значений равны между собой, а какие – нет. Это позволяет сделать метод множественных сравнений Шеффе (другое название — заключение о линейных контрастах по Шеффе) и LSD критерий. Необходимость в специальных критериях , а не использование существующих для проверки каждой пары недопустимо (см. примечания к 3.1). Недопустимость связана с тем, что мы желаем проверить выполнения нескольких условий одновременно. Дело в том, что ввиду зависимости таких проверок друг от друга доверительные интервалы (и, разумеется, результаты проверок на равенство) будут отличаться от сравнения любой пары средних отдельно.
Существуют другие подобные методы, например метод Тьюки и метод Стьюдента-Ньюмена-Кейлса, но они требуют специальных таблиц, имеющихся только в труднодоступной литературе.
Назначение. Проверка гипотезы о принадлежности нескольких средних значений к одной генеральной совокупности или выделение групп средних значений, принадлежащих к одной совокупности..
Нулевая гипотеза. H0 : , где ci определенные константы, причем на них налагается условие .
Предпосылки.
Распределение данных должно быть нормальным.
Данные независимы.
Краткие теоретические сведения.
В данном контексте контрастом называют линейную комбинацию средних значений средних выборок. Смысловое происхождение этих условий рассмотрим на примере. Допустим, у нас имеется 5 выборок, средние значения которых ,, , и . Если мы считаем, что эти выборки принадлежат к двум разным генеральным совокупностям, средние значения в которых исоответственно. Тогда нулевая гипотеза может быть сформулирована в виде H0:–=0. При этом в зависимости от состава выборок, из которых могут состоять группы A и B. Возможны следующие конкретные варианты этой гипотезы.
и далее варианты могут продолжить сами читатели.
Понятно, что загадочные коэффициенты Сi для первого случая имеют значения 1/2, 1/2, -1/3, -1/3, -1/3 , а для второго 1, -1/4, -1/4, -1/4, -1/4. Они будут зависеть от того, какие группы мы хотим проверить. Так, в первом случае, в одну группу входит первая и вторая выборка, а во вторую – третья, четвертая и пятая. Разумеется наиболее часто проверяются не группы, а отдельно взятые выборки. Например, если мы желаем сравнить между собой первую и четвертую выборки, то коэффициенты С будут иметь следующие значения 1, 0, 0, -1, 0. Таким образом, изменяя С, можно проверить любые комбинации пар выборок. Критериальное значение рассчитывается по следующей формуле
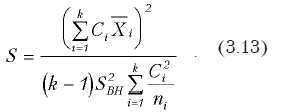
При этом внутригрупповая дисперсия рассчитывается по формуле
,
где , k – число выборок, ni – количество наблюдений в каждой выборке, – общее количество наблюдений. Если рассчитанное значение S будет больше критического значения распределения Fk-1,n-k,a, то гипотезы о равенстве средних соответствующих выборок или групп выборок отвергается.
Порядок выполнения сравнений
Для того, чтобы избежать противоречий в сравнениях (см. 3.2.8), необходимо придерживаться следующего порядка проведения сравнений.
Сначала средние значения упорядочиваются по величине. Затем проводится сравнение наибольшего среднего с наименьшим. Затем того же наибольшего среднего со следующим по величине наименьшим и т.д. до тех пор, пока очередная проверка приведет к принятию нулевой гипотезы о равенстве средних. После этого наибольшее среднее заменяется следующим по величине (наибольшим исключая самый большой). Все проверки снова проводятся начиная с самого маленького среднего значения.
Образование групп однородных средних
Часто возникает необходимость в проверке всех пар с целью выяснить, не образуют ли они некоторое количество однородных групп. Для этого используется критерий LSD (least significant difference) [5]. При этом необходимо выполнить следующие действия.
- Упорядочить средние значения выборок по убыванию.
- Для каждой соседней пары, начиная с первой выполнить проверки значимости разности средних. Для проверки рассчитывается значение Для случая одинакового количества наблюдений в каждой выборке используется формула:
Это значение будет использовано для проверок всех пар.
В ситуации, когда объемы выборок различаются, используется формула
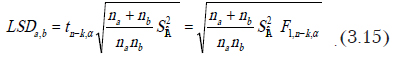
При этом значение критерия придется рассчитывать для каждой соседней пары.
Здесь tn-k,a – табличное значение критерия Стьюдента; – внутригрупповая дисперсия (см. выше); F1,n-k,a – табличное значение критерия Фишера; ni – количество наблюдений в каждой выборке (если выборки одинакового размера); na и nb – количества наблюдений в выборках, проверяемых на равенство средних; n – общее количество наблюдений; k – количество выборок.
Если разница средних значений соседней пары меньше значения LSD, то эти средние значения считаются одинаковыми, а соответствующие выборки объединяют в однородную группу.
Примечание.
При совместном применении множественных сравнений по Шеффе и критерия LSD возможно появление кажущихся противоречий. Например, средние значения выборок, входящих в разные однородные группы, отличаются друг от друга незначимо. Противоречия здесь на самом деле нет. В однородной группе собраны выборки, для совокупности средних которых принимается гипотеза об их равенстве. То же, что некоторые из них могут быть при парном сравнении быть равными средним из других выборок, никак этому не противоречит.
Пример.
На рис. 3.25 в ячейках B1:F14 помещены исходные данные для задачи, состоящие из пяти выборок.
В ячейках В15-В17 помещены формулы =СРЗНАЧ(B2:B14), =NORMSAMP_1(B2:B14) и =ЧСТРОК(B2:B14) соответственно, в которых вычисляется среднее значение, проверяется распределена ли выборка по нормальному закону и определяется число наблюдений. На ячейки С-F с номерами 15-17 формулы размножаются перетягиванием. В ячейке F18 помещаем значение n (общее количество наблюдений), которое вычисляется как =СУММ(B17:F17). В F19 помещается k (число выборок), получаемое по формуле =ЧИСЛСТОЛБ(B2:F2).
Формируем в ячейках H2:L14 вспомогательную матрицу. Для этого в ячейку H2 помещаем формулу =(B2-B$15)*(B2-B$15), которую затем размножаем перетягиванием на все ячейки указанного диапазона. Затем в ячейку L15 помещаем формулу для вычисления внутригрупповой дисперсии =СУММ(H2:L14)/(F18-F19).
Для того, чтобы выполнить попарные сравнения всех средних, в ячейках B21:F30 строим матрицу коэффициентов Сi. Как вы видите, она строится простым перебором всех вариантов комбинаций. Для средних, которые будут сравниваться, ставится 1 и –1, для всех остальных – 0. В столбце А указано, для сравнения средних каких выборок предназначена данная строка коэффициентов. Затем с помощью этой матрицы строится вспомогательная матрица H21:L30. Для этого в ячейку H21 помещается формула =B21*B$15, которая затем размножается перетягиванием на все ячейки указанного диапазона.
Затем строим столбец контрастов (для нашего случая фактически разницы пар средних) в столбце М. Для этого в ячейку M21 помещаем формулу =СУММ(H21:L21), размножаемую на весь столбец. В столбец N помещаются квадраты столбца разницы (формула =M21*M21 в N21, которая затем размножается перетягиваем). Последний столбец (О) содержит критериальные значения для каждой сравниваемой пары. Для этого в О21 помещается формула =N21/(($F$19-1)*$L$15*2/B$17), размножаемая затем на весь столбец.
В ячейке М33 помещено критическое значение F-распределения, рассчитываемое по формуле =FРАСПОБР(0,05;F19-1;F18-F19).
Теперь осталось сравнить критериальные значения и критическое и сделать выводы. Для этого в ячейку Р21 помещаем формулу =ЕСЛИ(O21<$M$33;»Одинаковы»;»Разные»). Размножаем ее на весь столбец. Теперь столбец Р содержит выводы для каждой пары сравниваемых средних.
Проведем теперь распределение средних по однородным группам. Для этого средние значения должны быть упорядочены по величине от большего к меньшего. Затем находится разница между соседними средними в упорядоченном ряду. Эти значения у нас уже есть в столбце М (см. таблицу 3.8). Необходимо только выбрать подходящие.
Таблица 3.8.
| Ячейка | B34 |
C34 |
D34 | E34 |
| Разница средних каких выборок | 1 и 2 | 2 и 3 | 3 и 4 | 4 и 5 |
| Из какой ячейки взята разница | М21 | М25 | М28 | М30 |
Затем рассчитывается значения LSD, для чего в ячейку М34 помещается формула =СТЬЮДРАСПОБР(0,05;F18-F19)*КОРЕНЬ(2*L15/B17).
Из сравнения видно, что средние распадаются на три однородные группы. В первую входит первая и вторая выборки, во вторую – третья, четвертая и пятая выборки составляют третью однородную группу.
Обратите внимание на тот факт, что средние значения для первой и второй выборок не отличаются статистически значимо друг от друга (строка 22), но при формировании групп входят в разные однородные группы!
Пример решения задачи о ценовых коридорах с использованием критерия Шеффе приведен в разделе 7.
3.3. Непараметрические критерии
Непараметрические критерии применяются в тех случаях, если закон распределения отличается от нормального, или данные измеряются в дискретных шкалах измерения.
Во всех случаях использования приведенных непараметрических критериев принимаются следующие допущения:
- все случайные величины взаимно независимы;
- анализируемые выборки распределены по непрерывному распределению одного и того же вида.
Очень часто проверяется гипотеза о равенстве не средних, а медиан. Это связано с тем, что для закона распределения, отличного от нормального, медиана является более устойчивой и корректной оценкой положения центра распределения.
Следует помнить, что непараметрические критерии имеют для случая нормального распределения мощность меньшую, чем соответствующие параметрические критерии. В связи с этим не следует использовать непараметрические критерии при нормальном распределении случайных величин в исследуемых выборках.
- Понятие о рангах и их построение
На практике довольно часто встречаются числовые данные в выборке носят в определенном смысле условный характер. Это могут быть экспертные оценки, тестовые балы, данные о каких-либо предпочтениях исследуемой группы людей (например, политических) и т.д. При анализе таких данных часто невозможно соблюсти все предпосылки применения классических статистических методов, которые подразумевают принадлежность рабочей выборки одному из известных законов распределения (например, нормальному). Иногда это очень трудно проверить или доказать (скажем, в силу недостаточного количества наблюдений). В таких случаях делать научно обоснованные выводы, применяя методы прикладной статистики, можно лишь используя не сами значения (например, баллы), а их порядок, основанный на соотношении “меньше – больше”. Порядок значений называют рангами. В литературе по статистическому анализу можно встретить несколько определений рангов. Приведем на наш взгляд, наиболее удачное: Рангом наблюдения называют номер, который получит это наблюдение в упорядоченной совокупности всех данных после упорядочения их согласно определенному правилу (например, от меньшего значения к большему).
В некоторых источниках понятие ранга приравнивается к понятию порядкового номера элемента вариационного ряда. Однако это верно лишь отчасти. Ведь в таком случае непонятно, каким образом поступать, если два или более элементов вариационного ряда равны между собой.
В дальнейшем при использовании понятия ранга, а также ранжирования (процесс присвоения элементам выборки рангов) мы будем подразумевать, что ряд значений ранжируется по правилу, основанному на соотношении “меньше – больше”.
Вариационным рядом называются значения случайной выборки (х1, х2, … хn), имеющие функцию распределения F(x) и расположенные в порядке их возрастания: х(1) < x(2) < … < x(i) < … < x(n), где i-й член вариационного ряда x(i) называется i-й порядковой статистикой, а номер члена вариационного ряда — рангом, порядком (статистики).
Ранжирование — это процедура перехода от совокупности наблюдений к последовательности их рангов. Результат ранжирования называется ранжировкой.
Рассмотрим процесс ранжирования на примере. Допустим, у нас есть выборка, состоящая из пяти чисел: 8, 25, 42, 3, 1. Этим значениям будут присвоены соответствующие следующие ранги: 3, 4, 5, 2, 1. По сути, они являются позициями элементов приведенной выборки, если ее отсортировать по возрастанию.
Иногда данные в выборке совпадают. Возникает вопрос: какой ранг присваивать совпадающим значениям выборки? В таком случае обычно используют так называемые средние ранги. Совокупность элементов выборки, имеющих одинаковое значение, называют связкой, а количество одинаковых значений в связке — ее размером. Средним рангом является среднее арифметическое тех рангов элементов связки, которые бы они имели, если бы одинаковые элементы связки оказались различны. Например, у нас есть выборка чисел: 15, 17, 12, 15, 7, 8, 5, 1, 8. Этим значениям будут соответствовать следующие ранги: 7,5; 9; 7,5; 6; 3; 4,5; 2; 1; 4,5.
Статистические методы, которые используют ранги для получения научно обоснованных выводов из анализируемых данных, называются ранговыми. Эти методы широко применяют там, где очень сложно (или невозможно) выяснить какому закону распределения соответствуют анализируемые данные. Однако следует отметить, что когда в анализируемых данных содержатся большие связки (или их много), применение этих методов вызывает сомнения. Если же количество связок невелико (и они не очень большие), то их необходимо учитывать в конкретных расчетных формулах.
Различные статистические пакеты имеют процедуры, позволяющие выполнить процесс ранжирования выборки, проще говоря — получить ранги элементов исследуемой выборки. Есть такая функция (РАНГ() RANK()) и в электронных таблицах Microsoft Excel. Но, к сожалению, работает она некорректно — не может назначать элементам выборки, при наличии в ней связок, средние ранги.
Далее приведена функция, реализованная на языке Visual Basic, которая позволяет решить задачу ранжирования выбранной выборки данных. Вы можете вставить модуль и аккуратно набрать (см. ниже) текст функции Rank1(). Будьте внимательны, так как небольшая ошибка (например, вы вместо запятой набрали точку с запятой) приведет к тому, что функция работать не будет.
Option Base 1
Function Rank1(x As Variant, R_1 As Object, t As Boolean) As Double
‘R_1 As Object, t As Boolean) As Double
‘подпрограмма, предназначенная для построения рангов
‘x — значение из массива (например, адрес ячейки памяти)
‘R_1 — массив (анализируемая выборка)
‘t — Ключ сортировки: 0 — по возрастающей; 1 — по убывающей
Dim mas1() As Double
Dim mas2() As Double
Dim tmas() As Double
num_elem = R_1.Count ‘количество элементов в выборке
‘создание массива для ранжирования рангов
‘Dim mas1 As Variant
‘mas1 = R_1.Value
ReDim mas2(num_elem)
ReDim mas1(num_elem)
ReDim tmas(num_elem)
‘Формирование копии исходного массива данных и массива для рангов
For i = 1 To num_elem
mas1(i) = R_1.Cells(i)
mas2(i) = i
Next i
‘Ранжирование массива данных (для сортировки используется ‘пузырьковый метод)
Counter = 1 ‘инициализация индикатора перестановок
While Counter = 1 ‘анализ значения индикатора перестановок
Counter = 0
For i = 1 To num_elem — 1
If mas1(i) > mas1(i + 1) Then tp = mas1(i): mas1(i) = mas1(i + 1): mas1(i + 1) = tp: Counter = 1
Next i
Wend
‘поиск связок среди ранжированного массива и корректировка
‘полученных рангов (назначение средних рангов)
i = 1
While i < num_elem
If mas1(i) = mas1(i + 1) Then ‘начало связки
k = i + 1
While mas1(i) = mas1(k)
k = k + 1
If k > num_elem Then GoTo NM
Wend
NM: aver_rank = (mas2(i) + mas2(k — 1)) / 2
For m = i To k — 1
mas2(m) = aver_rank
Next m
i = k — 1
End If
i = i + 1
Wend
‘поиск ранга заданного элемента выборки
For i = 1 To num_elem
If x = mas1(i) Then Rank1 = mas2(i)
Next i
End Function
Рассмотрим применение данной функции на примере. Допустим, у нас имеется ряд данных, полученных в результате медико-биологических исследований, который нам необходимо проранжировать (построить ранги значений выборки): {3,6; 4; 5,2; 4; 4,4; 4,7; 5,9; 3,4; 4; 5,5; 5; 4,2; 4} (рис. 3.26). Данные могут быть представлены как в виде столбца, так и в виде строки или матрицы (все ее строки и столбцы должны быть полностью заполнены, пустых ячеек быть не должно). Построение рангов выполняется в два этапа, при условии, что вышеописанная функция Rank1(x; R_1, t) уже введена. Параметры данной функции имеют следующее назначение: х — число (или ссылка на ячейку), ранг которого необходимо найти; R_1 — ссылка на диапазон ячеек, который необходимо проранжировать; t — параметр указывающий направление ранжирования и принимающий значение 0 или 1 (0 — ранжирование от меньшего к большему, 1 — ранжирование от большего к меньшему). Ссылку на ячейку для параметра х лучше делать относительной, а ссылки на диапазон ячеек для параметра R_1 — абсолютными.
- Вычислите значение ранга для первой ячейки вашего ряда данных. В нашем примере — ячейка А2. Для этого введем в ячейку В2 формулу =Rank1(A2; $A$2:$A$14, 1) и щелкнем по кнопке Enter строки формул (рис. 3.26). При указании на месте второго параметра данной функции, необходимо применять абсолютную адресацию (использовать знак “$”).
- Размножьте данную формулу для всего ряда данных. Это легко сделать, используя согласованное размножение формул с помощью мыши (см. подраздел “Согласованное размножение формул”). В результате этих действий мы построим ранги нашего ряда данных. Помните, что для размножения формул подобным образом необходимо, чтобы диапазон ячеек был указан с использованием абсолютных ссылок, иначе результаты, которые вы получите, будут неправильными.
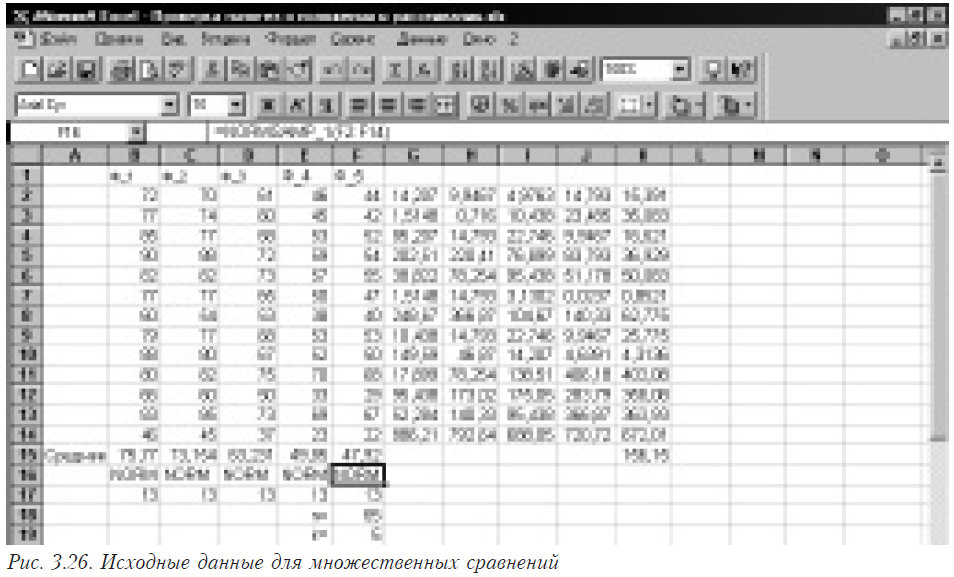
3.3.2. Критические значения статистики W критерия Уилкоксона
Критические значения статистики W критерия Уилкоксона широко применяется при использовании методов проверки статистических гипотез, основанных на рангах. Данные критические значения достаточно хорошо табулированы и приводятся в виде таблиц во многих литературных источниках. Но, не всегда под рукой есть необходимая книга. Поэтому, мы предлагаем использовать для расчета критических значений статистики W формулу, основанную на ее аппроксимации с использованием нормального распределения.
Нижняя критическая точка статистики W довольно точно вычисляется по аппроксимационной формуле.
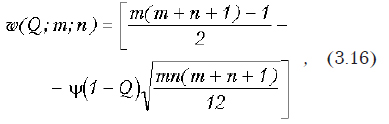
где [a] — округленная к ближайшему целому часть числа a; Q — уровень значимости для одностороннего критерия; m, n — размеры исследуемых выборок, причем m £ n, — значение обратной функции нормального распределения с параметрами (0, 1). Приведенная выше аппроксимационная формула дает удовлетворительные результаты при n ³ m ³ 5.
Верхняя критическая точка связана с нижней соотношением
![]()
Таким образом, зная нижнее критическое значение статистики W, всегда можно вычислить ее верхнее критическое значение.
Критическое значение статистики Манна — Уитни U связано с критическим значением статистики W соотношением
![]()
Например, если Q=0,05; m=10; n=12, то = w (0,05; 10; 12) – 10*(10+1)/2 = 89 – 55 = 34. Полученное значение соответствует приводимому в таблицах.
Вычисление критических значений статистики W в электронных таблицах Microsoft Excel можно выполнить двумя способами. Первый способ — прямо в ячейку таблицы можно ввести вышеприведенную формулу, использовав вместо встроенную в Microsoft Excel функцию НОРМСТОБР(1–Q) (NormSInv(1–Q)). Пример вычисления критических значений статистик приведен на рис. 3.27.
Второй способ заключается в том, чтобы автоматизировать вычисление критических значений статистики W, определив свою пользовательскую функцию Wperculc1(alfa; m_size; n_size) при помощи встроенного в Microsoft Excel языка программирования Visual Basic. Текст данной функции приведен ниже (правила определения пользовательских функций детально описаны в 1.6). Параметры данной функции имеют следующее назначение: alfa — задаваемый вами уровень значимости Q; m_size — размер одной выборки; n_size — размер второй выборки. Про задании конкретных параметров для данной функции нет разницы, размер какой выборки больше, так как она определяет это автоматически и выдает корректные результаты.
Function Wperculc1(alfa As Double, m_size As Double, n_size As Double) As Double
‘Функция расчета нижних процентных точек статистики ранговых сумм
‘Уилкоксона (работает довольно точно)
tmp_size = 0#
If(m_size>n_size) Then tmp_size=m_size: m_size=n_size: n_size= tmp_size
psi = 0#
psi = Application.NormSInv(1 — alfa)
m_tmp = m_size + n_size + 1
tp_1 = 0#
tp_2 = 0#
tp_3 = 0#
tp_1 = (m_size * m_tmp — 1) / 2
tp_2=(m_size^2 + n_size^2 + m_size * n_size + m_size + n_size)/ _
(20 * m_size * n_size * m_tmp)
tp_3 = Sqr(m_size * n_size * m_tmp / 12)
Wperculc1 = Application.Round(tp_1 — psi * tp_3, 0)
End Function
Пример
Вычислим, используя приведенные в данном подразделе формулы, критические значения статистик W и U при условии, что задан уровень значимости Q=0,05; одна выборка имеет размер m = 8; вторая — n = 10. При использовании вышеприведенных формул необходимо помнить, что m £ n, в противном случае соответствующие выборки можно поменять местами.
- Подготовим данные для выполнения последующих вычислений, введя требуемый уровень значимости и размеры выборок в соответствующие ячейки (см. рис. 3.27) электронной таблицы.
- Вычислим нижнее критическое значение статистики W:
а) при помощи формулы.
Введем в ячейку С6 следующую формулу:
=ОКРУГЛ((C4*(C4+C5+1)-1)/2-НОРМСТОБР(1-C3)*КОРЕНЬ(C4*C5*(C4+C5+1)/12); 0).
В результате будет вычислено нижнее критическое значение статистики W, равное в нашем случае 57 (см. рис. 3.27).
б) при помощи функции, определенной пользователем.
Определите (если вы не сделали этого ранее) свою пользовательскую функцию вычисления нижних критических значений статистики W Wperculc1(alfa; m_size; n_size. Используя Мастер функций или вручную введите в ячейку С7 следующую формулу: =Wperculc(C3;C4;C5). После окончания ввода формулы будет вычислено требуемое критическое значение (57) (см. рис. 3.27).
- Вычислим верхнюю критическое значение статистики W, используя приведенное в этом подразделе соотношение. Для этого в ячейку Е9 вставим формулу: =C4*(C4+C5+1)-C6. Вычисленное значение равно 95 (см. рис. 3.27).
- Вычислим критическое значение статистики U критерия Манна — Уитни. С этой целью в ячейку Е11 вставим формулу: =C6-C4*(C4+1)/2. Вычисленное значение равно 21 (см. рис 3.27).

3.3.3. Критерий Краскела — Уоллиса (Н-критерий)
Назначение. Проверка гипотезы о том, что несколько (k) выборок имеют одинаковое распределение и, следовательно, средние значения этих выборок равны между собой.
Нулевая гипотеза. Все k выборок имеют одинаковое распределение.
Альтернативная гипотеза. Нулевая гипотеза неверна.
Предпосылки. Все случайные величины взаимно независимы.
Описание метода
- Выборки объединяются в одну.
- Для объединенной выборки все наблюдения заменяются рангами (см. 3.3.1).
- Определяется критериальное значение по формуле: ,
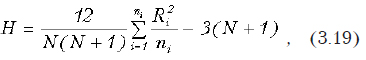
где N — общее количество наблюдений, определяемое следующим образом ;
ni — число наблюдений в каждой выборке; Ri — сумма рангов по каждой выборке (rij – ранг j-го наблюдения в i-й выборке); k — количество выборок. - Выполняется сравнение расчетного значения критерия с критическим (табличным) значением. В том случае, если расчетное значение критерия больше критического, то нулевая гипотеза отклоняется, и мы не можем считать, что средние равны между собой.
При малом общем числе опытов (N < 15) используются специальные таблицы распределения Краскала — Уоллиса (см. приложение В). Если общее количество опытов больше указанной величины, то в качестве критической используется верхняя 5% точка распределения c2 с (k-1) числом степеней свободы.
Примечание:
- Если нулевая гипотеза отклонена, то для того, чтобы выяснить, какие пары выборок имеют одинаковое распределение, нельзя использовать любые двухвыборочные критерии (см. подраздел о парадоксах в сравнении средних) — необходимо применять множественные сравнения.
- Этот критерий менее мощный, чем критерий Фишера, поэтому при числовых данных и нормальном законе распределения следует применять именно критерий Фишера или Кохрена для нескольких дисперсий.
- В тех случаях, когда выборки имеют разное распределение, данный критерий неприменим. Вместо него следует использовать критерий Фридмана (см. раздел 4).
- В том случае, когда в столбце наблюдений имеются связки, то значение критерия корректируется по формуле
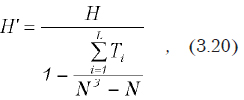
где L — количество связок, Ti — количество совпадающих элементов в i-й связке.
Пример
Исследуется эмбриотоксичность. На рисунке 3.28 в столбцах В, С и D приведены значения размеров плаценты животных трех групп (1, 5, 6). Группа 1 — интактные беременные животные; животным группы 5 на 10-й день болезни внутривенно вводился водный раствор эмбихина в дозе 0,4 мг/кг, а с 10-го по 20-й — масляный раствор a-токоферола ацетата в дозе 15 мг/кг; животным группы 6 на 10-й день болезни внутривенно вводился водный раствор эмбихина в дозе 0,4 мг/кг, а с 10 по 20-й — масляный раствор a-токоферола ацетата в дозе 10 мг/кг. Необходимо выяснить, можно ли считать средние значения всех групп равными, и следовательно, эффект обработки отсутствует. Для решения этой задачи выполняются следующие действия.

- Необходимо проверить, можно ли считать, что данные распределены по нормальному закону. Для этого в ячейках В16, С16 и D16 помещаем вызовы функции NORMSAMP_1.
| В16 | С16 | D16 |
| =NORMSAMP_1(В3:В12) | =NORMSAMP_1(C3:C12) | =NORMSAMP_1(D3:D14) |
- Ответ во всех трех случаях отрицательный, поэтому мы вправе применять ранговый критерий.
- Объединяем все три выборки в одну. Объединенная выборка занимает ячейки с F3 по F34.
- Для объединенной выборки строим ранги. Для этого в ячейке G3 помещаем вызов функции =Rank1(F3;$F$3:$F$34;1). Затем он размножается для всех ячеек от G4 до G34 (см. раздел 1).
- Результат дальнейшей работы представлен на рис. 3.29. Сначала мы находим суммы рангов для каждой выборки:
| I12 | I13 | I14 |
| =СУММ(G3:G12) | =СУММ(G13:G22) | =СУММ(G23:G34) |
- Желательно проверить правильность расчетов по рангам.
| G36 | G37 | G38 |
| =СУММ(G3:G34) | =СУММ(I12:I14) | =I16*(I16+1)/2 |
- Результаты всех этих действий должны быть одинаковы. Для данного примера — 528.
- Рассчитаем квадраты сумм рангов =I12*I12:
| J12 | J13 | J14 |
| =I12*I12 | =I13*I13 | =I14*I14 |
- Находим квадраты рангов, деленные на число экспериментов:
| K12 | K13 | K14 |
| =J12/ЧСТРОК(B3:B12) | =J13/ЧСТРОК(C3:C13) | =J14/ЧСТРОК(D3:D14) |
- Для использования в дальнейших расчетах в ячейку I16 помещаем значение N (общего числа наблюдений) =ЧСТРОК(B3:B12)+ ЧСТРОК(C3:C12)+ЧСТРОК(D3:D14).
- В ячейке I17 рассчитываем критериальное значение по формуле.: =(12/(I16*(I16+1)))*K15-3*(I16+1) Имейте в виду, что должно получится положительное значение.
- Поскольку общее число опытов больше 15, для получения табличного значения можно воспользоваться процентной точкой распределения c2. Для этого в ячейку I18 помещаем вызов функции =ХИ2ОБР(0,05;3-1). Здесь 3 — количество выборок, а 0,05 — уровень значимости.
- Так как расчетное значение критерия (см. п.11) меньше табличного (см. п.12), то нулевая гипотеза принимается. Следовательно, мы можем считать, что средние этих выборок равны и следовательно эффект обработки отсутствует.

В нашем примере много связок: 6 значений по 16; 9 по 15; 8 по 14; 7 по 13; 2 по 12. Таким образом, L = 5, а массив Ti = {6,9,8,7,2}. Тогда скорректированное значение критерия определяется следующим образом:
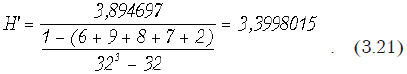
При скорректированном значении наши выводы не меняются.
3.3.4. Критерий Зигеля — Тьюки
Назначение.
Предназначен для проверки равенства дисперсий двух выборок для порядковых данных или при законе распределения выборок, отличающемся от нормального.
Нулевая гипотеза. .
Предпосылки.
- Все случайные величины взаимно независимы.
- Анализируемые выборки распределены по непрерывному распределению одного и того же вида.
Краткие теоретические сведения
Проверяется гипотеза о принадлежности двух независимых выборок к одной генеральной совокупности. Для этого формируют объединенную выборку с общим числом наблюдений n1 + n2 (при этом n1 < n2), которая упорядочивается по величине. Затем формируются ранги (Внимание! Ранги строятся необычным образом!) таким образом, что минимальные и максимальные значения получают низкие ранги, а по мере приближения к средним значениям ранги увеличиваются. При этом, если наблюдений нечетное количество, то среднее наблюдение (медиана) не получает никакого ранга. Ранг 1 присваивается наименьшему значению, ранги 2 и 3 двум наибольшим, 4 и 5 следующим наименьшим, 6 и 7 следующим наибольшим и т.д. Затем для каждой выборки определяют суммы присвоенных рангов R1 и R2. Для проверки правильности расстановки рангов можно воспользоваться выражением R1 + R2 = (n1+n2)(n1+n2+1)/2 для нечетного общего количества наблюдений или R1 + R2 =(n1+n2)((n1+n2+1)/2–1) для четного.
Для малых объемов выборки (n1 £ n2 £ 20) существуют специальные таблицы, которые дают критические значения распределения Уилкоксона . В тех случаях, когда n1, n2 > 9 или n1 > 2, n2 > 20, можно применять стандартную нормальную переменную
где R1 — сумма рангов меньшей по объему выборки. Когда 2R1 > n1 (n1+n2+1), в числителе выражения для z перед 1 знак нужно заменить “+” на “–”.
Если объемы выборок очень отличаются, z необходимо скорректировать:
![]()
В случае, если больше 20% наблюдений (разных выборок!) связаны равенствами или зависимостями, знаменатель выражения для z принимает следующий вид:
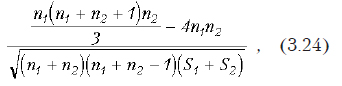
где S1 — сумма квадратов рангов зависимых наблюдений, а S2 — сумма квадратов средних рангов зависимых наблюдений (в каждой группе зависимых наблюдений находится средний ранг).
По вычисленному значению z из таблицы определяем вероятность, умножив которую на 2 получим уровень значимости a. Если эта вероятность мала (меньше 0,05), то с доверительной вероятностью 1 – a можно считать, что присутствует разница дисперсий генеральных совокупностей.
Примечание:
- Чем больше различаются выборки, тем менее надежен этот критерий.
Пример
Обратимся к примеру из предыдущего параграфа и проверим гипотезу о равенстве дисперсий. На рис. 3.30 показаны исходные данные в столбцах В и С. Столбец F — объединенная выборка, а E — вспомогательный столбец, в котором хранится номер, показывающий, из какого исходного столбца получено данное значение (1 для В и 2 для С).
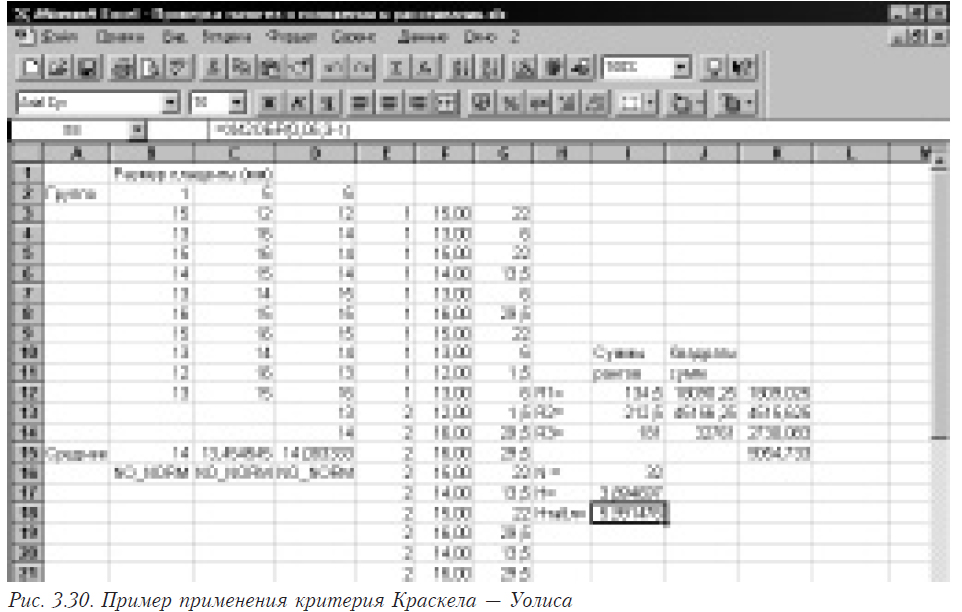
Необходимо выполнить следующие действия:
- отметить столбцы E и F;
- выбрать в меню пункт Данные;
- выбрать в появившемся подменю пункт Сортировка
- В появившемся окне установить “Столбец Е” для сортировки, а затем — “По убыванию”. После этого выбрать ОК.
В результате мы получим упорядоченный по величине столбец F. При этом столбец Е сохранит связь с ним, и будет указывать, из какой выборки взяты соответствующие значения. Результат работы приведен на рис. 3.31.

После этого мы вручную строим ранги так, как описано выше. Результат построения рангов приведен на рис. 3.32 и 3.33.


Далее для определения значений R1 и R2 необходимо построить два вспомогательных столбца — G и H. Для этого в ячейку G3 помещается формула =ЕСЛИ(D3=1; F3; 0), которая затем размножается на весь столбец. А в ячейку H3 вводится формула =ЕСЛИ(D3=2; F3; 0), которая также размножается на весь столбец. Результат приведен на рис. 3.34.

Затем определяем значение R1, поместив в ячейку Н26 формулу =СУММ(G3:G24), а введя в ячейку Н27 формулу =СУММ(H3:H24), находим R2.
Для проверки правильности вычисления этих значений в ячейку Н30 вводим формулу =СУММ(H26:H27), а в ячейку I30 формулу для четного общего количества наблюдений =(ЧСТРОК(B3:B12)+ЧСТРОК(C3:C14))*((ЧСТРОК(B3:B12)+ЧСТРОК(C3:C14)+1)/2-1). Полеченные значения в обеих ячейках должны совпадать.
После этого рассчитываем значение z, для чего в ячейку Н31 помещается следующая формула =(2*H26-ЧСТРОК(B3:B12)*(ЧСТРОК(B3:B12) +ЧСТРОК(C3:C14)+1) +1) /КОРЕНЬ(ЧСТРОК(B3:B12)*(ЧСТРОК(B3:B12) +ЧСТРОК(C3:C14)+1)*ЧСТРОК(C3:C14)).
Далее с помощью формулы =2*НОРМРАСП(H31;0;1;ИСТИНА), помещенной в ячейку Н31, рассчитываем вероятность отвержения нулевой гипотезы, если она верна. Поскольку это значение (0,261418) существенно больше уровня значимости (0,05), нулевая гипотеза о равенстве дисперсий выборок принимается. Результат приведен на рис. 3.35.
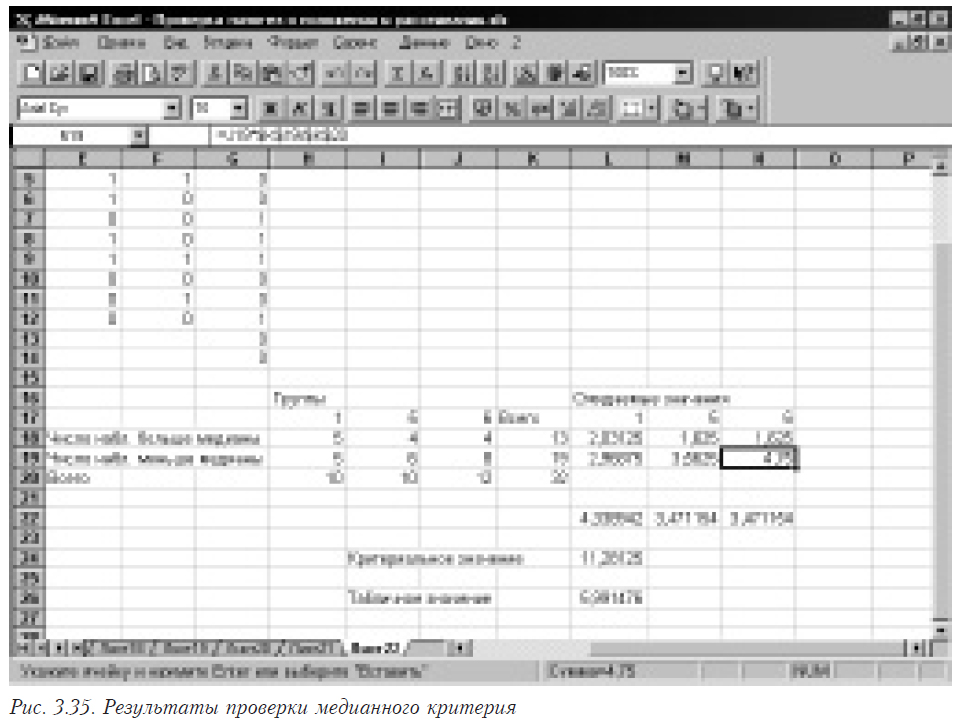
3.3.5. Критерий знаков
Назначение. Применяется в тех случаях, когда сравниваемые выборки одинакового размера и естественным образом разбиваются на пары (связанные выборки). Например, показатели одних и тех же больных до приема препарата и после; показатели роста или урожайности пары кустов, растущих рядом, при этом один из пары получает дополнительную подкормку или обработку. Иногда такие проверки называют проверкой наличия эффекта обработки.
Нулевая гипотеза. Фактически проверяется гипотеза о равенстве нулю медианы разности между парами двух выборок.
Краткие теоретические сведения
Рассчитываются значения
где Xi и Yi — значения элементов соответствующих выборок.
Поскольку предполагается, что совместное распределение Х и У непрерывно, то вероятность равенства значений Х и У считается равной нулю. Поэтому, в случае совпадения значений они отбрасываются, и количество измерений соответственно уменьшается. Вычисляется число m, равное количеству Zi, значения которых равны 1.
Для небольших выборок можно вычислить уровень значимости (вероятность отвергнуть гипотезу о равенстве нулю медианы разности, если она верна) по формуле
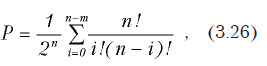
где n — размер выборки.
Для больших выборок можно воспользоваться приближенной нормальной аппроксимацией

Если полученное значение Р мало (меньше 0,05), то гипотеза о равенстве нулю отвергается.
В тех случаях, когда размеры выборок не равны или естественное разбиение на пары невозможно, применяется медианный критерий для двух выборок или двухвыборочный критерий Уилкоксона.
Пример
Пример для критерия знаков подробно рассмотрен в разделе 3.1.5.
3.3.6. Критерий Манна — Уитни
(U-критерий Уилкоксона, Манна, Уитни)
Назначение. Проверка гипотезы о равенстве средних двух независимых выборок.
Нулевая гипотеза. Н0: две независимые выборки принадлежат одной генеральной совокупности, их функции распределения равны. Эта гипотеза включает равенство средних и медиан.
Может проверятся и другая гипотеза: , где А — некоторая константа. Чтобы применить эту гипотезу, необходимо из всех наблюдений первой выборки вычесть А, а остатки считать новой первой выборкой. После этого все описанные ниже действия выполняются аналогично.
Предпосылки
- Все случайные величины взаимно независимы.
- Наблюдения, входящие в одну выборку, принадлежат к одной генеральной совокупности.
- Дисперсии выборок равны.
Краткие теоретические сведения
Этот критерий — непараметрический аналог t-критерия для проверки средних значений.
Является самым строгим из непараметрических критериев. Может применяться только в случае, когда дисперсии выборок равны.
Формируется единая выборка, для ее значений определяются ранги (по возрастанию). Повторяющимся наблюдениям присваивается средний ранг (см. раздел 3.3.1).
Определяется расчетное значение критерия.
Для малых выборок:
![]()
![]()
Здесь R1 и R2 — суммы рангов, рассчитанных для значений, принадлежащих первой и второй выборкам соответственно.
Правильность расчета U1 и U2 проверяется соотношением
![]()
Критериальное значение определяется следующим образом:
![]()
Гипотеза о равенстве выборок отвергается, если U > U(n1, n2, a), где U(n1, n2, a) — критическое значение статистики Манна — Уитни (таблица из приложения А). Кроме того, в подразделе 3.3.2 подробно изложено, каким образом можно довольно точно вычислить критическое значение статистики U через критические значения статистики W.
Для выборок, размер которых достаточно велик (n1 + n2 > 60), можно воспользоваться аппроксимацией
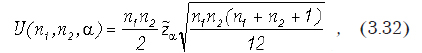
где соответствует значению стандартного нормального распределения. Для случая n1 ³ 8 и n2 ³ 8 можно воспользоваться нормальной аппроксимацией:
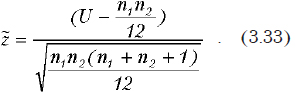
Если рассчитанное значение больше табличного значения нормального стандартного распределения, взятого с соответствующим уровнем значимости, то гипотеза отвергается.
Примечание:
- Внимание! Если нулевая гипотеза отвергается, значит, что выборки имеют разные законы распределения. Но в общем случае это не означает, что средние значения не равны.
- Критерий малочувствителен к малым различиям дисперсий выборок.
- t-критерий мощнее критерия Манна — Уитни, поэтому последний не следует использовать в случае нормального распределения выборок.
- Этот критерий нельзя применять к связанным выборкам.
- Из предполагаемой непрерывности распределений анализируемых выборок следует отсутствие повторов в выборках. Однако на практике совпадения встречаются довольно часто, что связано, например, с округлением данных при измерении. В этом случае сделанные при помощи этого критерия выводы, являются приблизительными (при этом, чем больше в выборках совпадающих значений, тем сомнительнее выводы). При большом количестве повторов данный метод применять не стоит, лучше воспользоваться, например, двухвыборочным критерием Уилкоксона.
Пример
В рассматриваемом примере исследуется эмбриотоксичность. Показателем является масса плаценты животных двух групп с условными номерами 4 и 6, подвергавшихся различной обработке.
- В первую очередь, необходимо проверить является ли закон распределения выборки нормальным.
- Поскольку одна из выборок имеет закон распределения, отличный от нормального, мы должны использовать непараметрический критерий. Для этого в столбце D формируем объединенную выборку.
- В столбце Е формируем ранги для объединенной выборки. Для этого в ячейку Е3 помещаем вызов функции =Rank_1(D3; $D$3:$D$34; 1), а затем размножаем его для всего столбца (рис. 3.36).

- Выполняем расчеты всех необходимых значений для проверки гипотезы. Необходимые формулы и функции приведены в таблице 3.9. Результат работы отражен на рис. 3.37.
Таблица 3.9
| Номер | Код столбца | Комментарий | |
| строки | F | G | |
| 7 | R1= | =СУММ(E3:E12) | Сумма рангов значений, принадлежащих первой выборке |
| 8 | R2= | =СУММ(E13:E24) | Сумма рангов значений, принадлежащих второй выборке |
| 10 | U1= | =ЧСТРОК(B3:B12)*ЧСТРОК(C3:C14)+ЧСТРОК(B3:B12)*(ЧСТРОК(B3:B12)+1)/2-G7 | Расчетное значение критерия для первой выборки |
| 11 | U2= | =ЧСТРОК(B3:B12)*ЧСТРОК(C3:C14)+0,5*ЧСТРОК(C3:C14)*(ЧСТРОК(C3:C14)+1)-G8 | Расчетное значение критерия для второй выборки |
| 12 | U | =НАИМЕНЬШИЙ(G10:G11;1) | Критериальное значение |
| 14 | U1+U2= | =G10+G11 | Проверка правильности |
| 15 | n1*n2= | =ЧСТРОК(B3:B12)*ЧСТРОК(C3:C14) | расчетов (значения в этих строках должны совпадать) |

Поскольку число наблюдений мало, необходимо воспользоваться таблицей распределения Манна — Уитни для принятия решения. Табличное значение для уровня значимости 0,05 и чисел степеней свободы 10 (n1) и 12 (n2) — 34. Поскольку рассчитанное значение U больше табличного — 59, нулевая гипотеза о равенстве средних исследуемых выборок отвергается.
3.3.7. Медианный критерий для нескольких выборок
Назначение. Используется для проверки принадлежности К выборок к одной генеральной совокупности. С точки зрения экспериментатора — эта проверка одновременного равенства друг другу медиан нескольких выборок.
Нулевая гипотеза. Все совокупности, из которых получены выборки, имеют одинаковый закон распределения (следовательно, медианы одинаковы ).
Предпосылки
- Все случайные величины взаимно независимы.
- Наблюдения, входящие в одну выборку, принадлежат к одной генеральной совокупности.
Краткие теоретические сведения
Сначала находят медиану объединенной выборки и после этого формируют таблицу, форма которой соответствует табл. 3.10.
Вычисляют ожидаемое число наблюдений для каждой клетки (при выполнении нулевой гипотезы). Для этого элемент строки “Всего” (соответствующий данной клетке) умножают на элемент столбца “Всего” (этой же клетки) и делят на общее число наблюдений n. Затем вычисляется расчетное значение критерия по формуле
c2 = S (наблюдаемое значение — ожидаемое значение)2 / ожидаемое значение.
Сумма находится по всем 2К клеткам таблицы.
Таблица 3.10
| Выборка 1 | Выборка 2 | … | Выборка К | Всего | |
| Число наблюдений, которые больше медианы | L1 | L2 | … | LK | |
| Число наблюдений, которые меньше медианы | n1 — L1 | n2 — L2 | … | nK — LK | n — |
| Всего | n1 | n2 | … | nK | n |
Ожидаемое значение для первой строки (в которой находятся значения Li) определяется по формуле

Для второй строчки (в которой находятся значения (ni-Li) ожидаемое значение определяется по формуле

Если рассчитанное значение c2 больше верхнего критического значения распределения c2, взятого с выбранным уровнем значимости a и числом степеней свободы (К-1), то гипотеза о равенстве средних отвергается.
Пример
Есть данные о размерах плаценты для трех выборок (см. рис. 3.38).
Для проверки гипотезы о равенстве медиан этих выборок необходимо выполнить следующие действия.
- Определяем медианы для всех трех выборок. Для этого в В17, С17, D17 помещается формулы =МЕДИАНА(B3:B12), =МЕДИАНА(С3:С12), =МЕДИАНА(D3:D12) соответственно.
- В столбцах F, G, H помещаем единицы, если значение наблюдения больше медианы, в противном случае — нули. Это можно сделать с помощью формул =ЕСЛИ($B3>$B$17;1;0), =ЕСЛИ($С3>$С$17;1;0), =ЕСЛИ($D3>$D$17;1;0), которые вводятся в ячейки F3, G3 и H3, а затем размножаются на все соответствующие столбцы. Результат приведен на рис. 3.38.
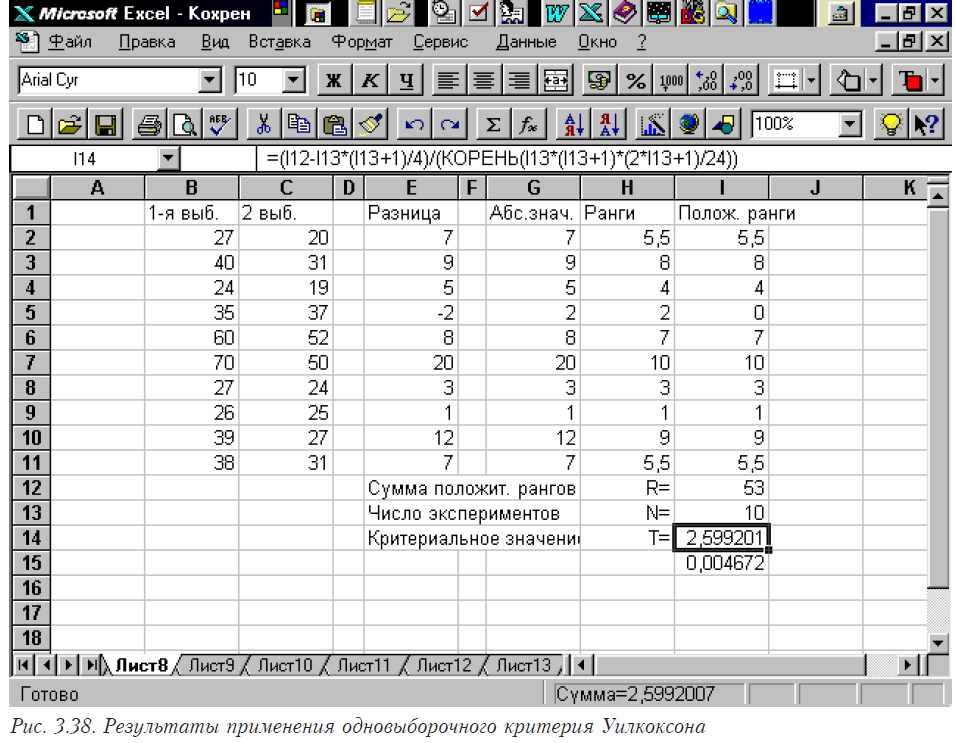
- Формируем необходимую нам таблицу.
| Строки /столбцы | Выборка 1 (I) | Выборка 2 (J) | Выборка 3 (K) | Всего(L) |
| Число наблюдений, которые больше медианы (18) | =СУММ(F3:F12) | =СУММ(G3:G12) | =СУММ(H3:H14) | =СУММ(I18:K18) |
| Число наблюдений, которые меньше медианы (19) | =J20-J18 | =K20-K18 | =K20-K18 | =СУММ(I19:K19) |
| Всего (20) | =ЧСТРОК(B3:B12) | =ЧСТРОК(C3:C12) | =ЧСТРОК(D3:D14) | =СУММ(I20:K20) |
- Формируем таблицу из расчетных ожидаемых значений.
Столбец |
M | N | О |
| Строка | 1 | 5 | 6 |
| 18 | =I18*$L$18/$L$20 | =J18*$L$18/$L$20 | =K18*$L$18/$L$20 |
| 19 | =I19*$L$19/$L$20
|
=J19*$L$19/$L$20 | =K19*$L$19/$L$20 |
| 22 | =(I18-M18)*(I18-M18)/M18 | =(J18-N18)*(J18-N18)/N18 | =(K18-O18)*(K18-O18)/O18 |
- Рассчитывается критериальное значение по формуле =СУММ(M22:O22), введенной в ячейку М24 .
- С помощью функции =ХИ2ОБР(0,05;3-1) вычисляем табличное значение для сравнения с критериальным. Вызов функции помещен в ячейку М26. Поскольку критериальное значение больше табличного, то нулевая гипотеза отвергается. Результат приведен на рис. 3.39.

3.3.8. Двухвыборочный критерий Уилкоксона
Назначение. Проверка гипотезы о равенстве средних двух независимых выборок.
Нулевая гипотеза. H0: Обе выборки имеют одинаковое распределение, то есть извлечены из одной генеральной совокупности. Следствием чего является равенство двух средних.
Предпосылки. Все случайные величины взаимно независимы.
Краткие теоретические сведения
Анализируемые выборки могут быть различных размеров — n1 и n2, причем n1 £ n2. Если же n1 > n2, то выборки следует поменять местами. Для дальнейшего анализа эти выборки объединяют в одну, размер которой будет n1 + n2. Для объединенной выборки строят ранги и рассчитывают значения сумм рангов, соответствующих обеим выборкам — R1 и R2.
Если размеры выборок одинаковы, то критериальное значение W будет равно одной из сумм рангов — R1 или R2. Если же выборки не равны, то в качестве критериального значения берется сумма рангов, соответствующих меньшей выборке (Wнабл.= R1).
Далее необходимо принять или отвергнуть нулевую гипотезу, воспользовавшись одним из трех способов.
Способ 1
Вычисленное критериальное значение Wнабл. сравнивается с верхним (W(Q, n1, n2)) и нижним (w(Q, n1, n2)) критическими значениями статистики Уилкоксона. Для малых значений выборок существуют специальные таблицы. Но их можно довольно точно рассчитать самостоятельно. Расчет критических значений статистики W детально рассмотрен в подразделе 3.3.2.
Гипотеза о равенстве средних отвергается на уровне значимости Q, если рассчитанное критериальное значение Wнабл. £ w( a, n1, n2) или Wнабл. ³ W( a, n1, n2), где a = Q/2.
Способ 2
Данный способ лучше применять для больших выборок, размер каждой из которых превышает 25. В этом случае от вычисленного значения Wнабл. переходят к W*, которое рассчитывается по формуле
Если вычисленное критериальное значение |W*| больше значения стандартного нормального распределения za, найденного для уровня значимости a= Q/2, то нулевая гипотеза о равенстве отвергается на уровне значимости Q.
Следует помнить, что этот способ можно использовать только в том случае, если размер хотя бы одной из выборок превышает 25 (при неравных выборках). Если размеры выборок равны, то данная аппроксимация хорошо работает при n1 = n2 = 8.
Если в выборках есть одинаковые значения (связки), то критериальное значение W* рассчитывается по формуле
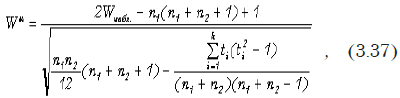
где k — число только тех групп связок, в которые входят ранги как одной так и второй выборок, ti — размер i-ой связки.
Способ 3
Этот способ связан с вычислением наименьшего уровня значимости pгр. Наименьшим уровнем значимости называется такой уровень, выше которого можно принять нулевую гипотезу если она верна. Для сформулированной нами нулевой гипотезы о равенстве средних наименьший уровень значимости вычисляется по формуле
![]()
где Ф(u) — функция нормального стандартного распределения (функция Лапласа). Если вычисленный наименьший уровень значимости очень мал, то нулевую гипотезу следует отвергнуть.
Пример
Предположим, нам необходимо выяснить, различаются ли статистически значимо результаты влияния различных способов антиагрегантного лечения на функциональную активность тромбоцитов при стабильной стенокардии. В качестве показателя используется тромбоцитарный тромбопластин. Наша задача — подтвердить или отвергнуть нулевую гипотезу о равенстве средних данного показателя для пациентов контрольной и экспериментальной групп. В таблице 3.11 приведены исходные данные.
Таблица 3.11 Исходные данные
| Контрольная группа | Экспериментальная группа |
| 27 | 55 |
| 41 | 24 |
| 34 | 40 |
| 44 | 60 |
| 69 | 39 |
| 38 | 28 |
| 24 | 22 |
| 30 | 37 |
| 37 | 72 |
| 59 | 42 |
| 43 | 33 |
| 39 | 41 |
| 25 |
- При помощи функции NORMSAMP_1 (R_1) (см. 3.15.) проверяем имеющиеся данные (по каждому столбцу отдельно) на соответствие их нормальному распределению. Для этого в ячейку А18 необходимо ввести формулу =NORMSAMP_1(A5:A16), а в ячейку В18 — =NORMSAMP_1(B5:B17). В результате мы выясним, что значения контрольной и экспериментальной выборок не распределены по нормальному закону (NO_NORM) (рис. 3.40) что подтверждает правильность применения в данном случае рассматриваемого критерия.

- Ведем размеры обеих выборок N1 и N2, а также уровень значимости Q. В нашем случае N1=12, N2 =13, Q = 0,05.
- Вычислим верхнее и нижнее критические значения статистики W, используя формулы и пользовательскую функцию, описанные в подразделе 3.3.2. Для этого необходимо определить пользовательскую функцию Wperculc1(alfa; m_size; n_size), если вы не сделали этого ранее. Далее в ячейку D8 введем формулу =Wperculc1(D7/2;D5;D6) для расчета нижнего критического значение статистики W, а в ячейку D10 — формулу =D5*(D5+D6+1)-D8 для расчета верхнего критического значение статистики W. В результате получим — w(a, n1, n2) = 119, W( a, n1, n2) = 193.
- Рассчитаем критериальное значение Wнабл.. Для упрощения этого процесса определим пользовательскую функцию W_crit1(R_1; R_2), текст которой на языке Wisual Basic приведен ниже. Параметры данной функции имеют следующее назначение: R_1 — диапазон ячеек первой выборки; R_2 — диапазон ячеек второй выборки. Ввод пользовательских функций детально описан 1.6. Наберите текст данной функции в отдельном модуле. Затем в ячейку D9 необходимо ввести формулу =W_crit1(A5:A16;B5:B17), использующую данную функцию. В результате получим — = Wнабл. = 161. На основе этого мы можем принять нулевую гипотезу, так как w(a, n1,n2) < Wнабл.< W( a, n1, n2). Полученные результаты приведены на рис. 3.41.
Option Base 1
Function W_crit1(R_1 As Object, R_2 As Object) As Double
‘Критериального значения статистики Уилкоксона для сравнения двух
‘независимых выборок
‘R_1 — контрольная выборка
‘R_2 — экспериментальная выборка
Dim m_t()
Dim group()
Dim rank_m()
Dim link_mas()
N_1 = R_1.Count ‘вычисление количества элементов в выборке
N_2 = R_2.Count ‘вычисление количества элементов в выборке
n_r = N_1 + N_2
ReDim m_t(n_r) ‘Совмещенная выборка
ReDim group(n_r) ‘Признаки 1 — выборка R_1, 2 — выборка R_2
ReDim rank_m(n_r) ‘Ранги выборки
ReDim link_mas(n_r / 2)
‘1. Формирование совмещенной выборки и массива признаков
‘ и инициализация массива рангов
For i = 1 To n_r
If i <= N_1 Then
m_t(i) = R_1.Cells(i)
group(i) = 1
Else
m_t(i) = R_2.Cells(i — N_1)
group(i) = 2
End If
rank_m(i) = i
Next i
‘2. Построение рангов совмещенной выборки
Counter = 1 ‘ Инициализация индикатора перестановок.
While Counter = 1 ‘ Анализ значения индикатора перестановок.
Counter = 0
For i = 1 To n_r — 1
If m_t(i) > m_t(i + 1) Then
tp = m_t(i): m_t(i) = m_t(i + 1): m_t(i + 1) = tp: Counter = 1
gr_t = group(i): group(i) = group(i + 1): group(i + 1) = gr_t
End If
Next i
Wend
‘Поиск связок среди ранжированного массива и корректировка рангов
i = 1
flag = 0: flag2 = 0
num_link = 0
While i < n_r
If m_t(i) = m_t(i + 1) Then ‘начало связок
K = i + 1
While m_t(i) = m_t(K)
If group(K — 1) <> group(K) Then flag = 1: flag2 = 1
K = K + 1
If K > n_r Then GoTo nm
Wend
nm: aver_rank = (rank_m(i) + rank_m(K — 1)) / 2
If flag = 1 Then num_link = num_link + 1: link_mas(num_link) = K — 1
For m = i To K — 1
rank_m(m) = aver_rank
Next m
i = K — 1
End If
i = i + 1
Wend
‘3.Вычисление суммы рангов меньшей выборки
R_sum = 0#
flag3 = 1
If N_1 >= N_2 Then flag3 = 2
For i = 1 To n_r
If group(i) = flag3 Then R_sum = R_sum + rank_m(i)
Next i
‘4.Вычисление критериального значения
W_crit1 = R_sum
End Function
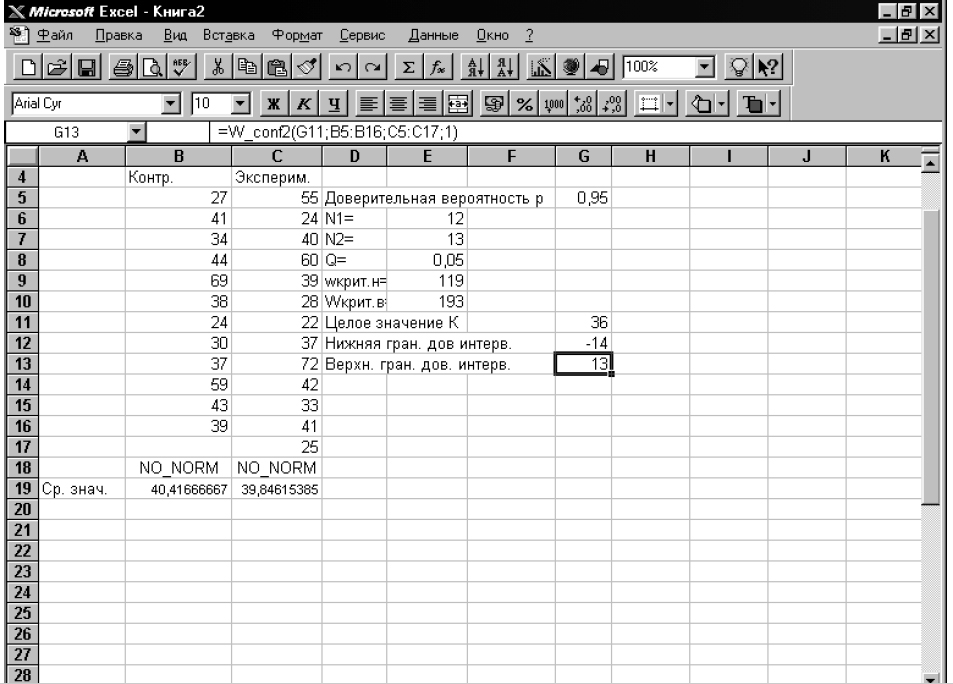
3.3.9. Критерий Уилкоксона для парных наблюдений (одновыборочный критерий Уилкоксона, критерий знаковых рангов)
Назначение. Аналог t-критерия для парных наблюдений в случае нечисловых данных или закона распределения, отличного от нормального. Применяется для связанных пар наблюдений (проверка отсутствия эффекта обработки).
Нулевая гипотеза. Распределение разностей пар симметрично относительно нуля.
Альтернативная гипотеза. Нулевая гипотеза неверна.
Предпосылки
- Разности независимы, принадлежат непрерывной совокупности (необязательно одной и той же), симметричной относительно нуля.
Краткие теоретические сведения
Для использования критерия необходимо:
- Рассчитать значения разностей пар двух выборок.
- Проранжировать абсолютные значения разностей пар в возрастающем порядке.
- Назначить им соответствующие значения рангов от 1 и выше. Нулевые разности не рассматриваются (отсюда — уменьшение общего количества наблюдений N). В общем, построение рангов выполняется как обычно (см. 3.1), только знаки разностей при этом не учитываются).
- Знаком считать ранга знак соответствующей ему разности.
- Посчитать сумму R положительных рангов.
- Вычислить критериальное значение:

- Проверить критерий. Для малых выборок (N < 20), если значение R больше табличного значения критерия знаковых рангов Уилкоксона Т+ (не следует путать со статистикой ранговых сумм W!), с уровнем значимости a/2 и числом степеней свободы N, нулевая гипотеза отвергается (таблицу для проверки критерия см. в приложении Б). Для больших выборок значение Т сравнивается с верхней a% точкой стандартного нормального распределения.
Другие гипотезы
H0: Средняя разница между значениями пар двух выборок равна А (заданная константа).
H1: Средняя разница неравна А.
В этом случае из каждой полученной разности вычитается А. Дальнейшая обработка выполняется по уже известной вам схеме (см. выше)
Примечание:
- Данный критерий устойчив к умеренным отклонениям от принятых предпосылок.
- Критерий Уилкоксона не следует применять к нормально распределенным совокупностям. Лучше использовать более мощный t-критерий.
- При наличии связок в формуле расчета критериального значения знаменатель рекомендуется заменить на выражение
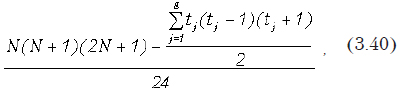
где g — количество связок, t1, …, tg — их размеры.
Пример
Воспользуемся примером, который был рассмотрен в 3.1.5. Помните, что на практике для анализа одних и тех же данных не используют несколько критериев одновременно — только один.
Столбцы В и С содержат показатели до и после лечения (соответственно) для одних и тех же больных. Для использования критерия необходимо выполнить следующие операции.
- В столбец Е помещаем разницу между столбцами В и С. Для этого в ячейку Е2 вводим формулу =B2–C2, которую затем размножаем для всех строк (см. раздел 1).
- В столбце G помещаем абсолютные значения разностей. Для этого в ячейку G2 вводим формулу =ABS(E2), которую затем размножаем для всех строк.
- Для абсолютных значений разностей формируем значения рангов. Для этого в ячейку Н2 помещаем вызов функции =Rank1(G2;$G$2:$G$11;1), который размножим для всех ячеек столбца (до 11-й включительно).
- Формируем вспомогательный столбец I, чтобы в дальнейшем найти сумму рангов, для которых соответствующая разность положительна. Для этого в ячейку I2 помещаем формулу =ЕСЛИ(ЗНАК(E2)=1;H2;0), а затем размножаем ее для всех строк столбца. В результате в столбец I помещаются значения рангов из столбца H, если соответствующая разность в столбе Е положительна. При отрицательной разности в ячейку столбца I помещается 0.
- Находим сумму положительных рангов, для чего в ячейку I12 помещаем формулу =СУММ(I2:I11).
- Для дальнейшего использования в расчетах в ячейку I12 помещаем значение числа наблюдений, которое определяется по формуле =ЧСТРОК(B2:B11).
- Определяем критериальное значение. Для этого в ячейку I14 помещаем формулу =(I12-I13*(I13+1)/4)/(КОРЕНЬ(I13*(I13+1)*(2*I13+1)/24))
- Определяем расчетное значение уровня значимости. В ячейку I15 помещаем вызов функции =1-НОРМСТРАСП(I14). Результаты выполненных операций приведены на рис. 3.42.
Поскольку при использовании критерия Т+ для малых выборок значение R (равное 53) больше, чем критическое (равное 47), полученное из таблицы приложения Г, для числа степеней свободы 10 и уровня значимости 0,024, нулевая гипотеза о равенстве средних отвергается.
Если мы воспользовались нормальной аппроксимацией для больших выборок, то полученное значение вероятности (0,004672) меньше уровня значимости (0,05), поэтому гипотеза отвергается.
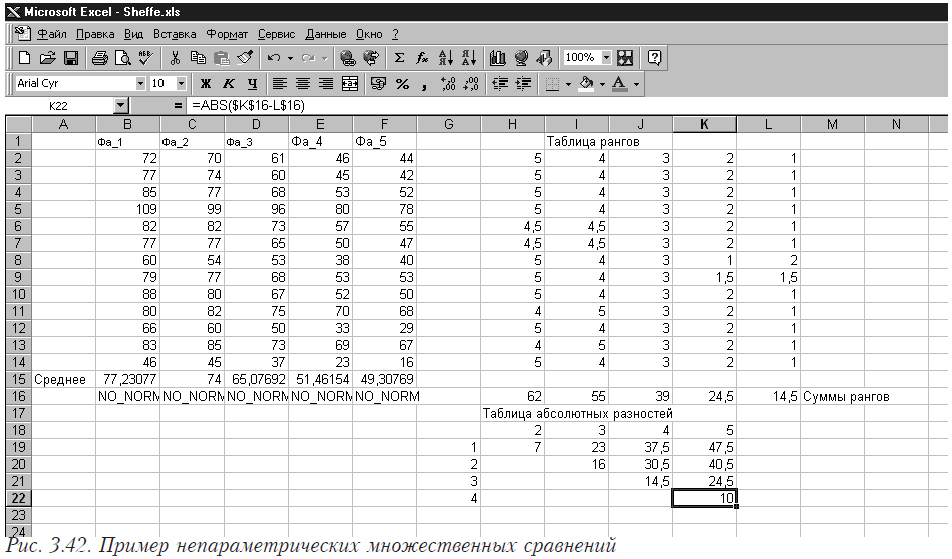
3.3.10. Медианный одновыборочный критерий (медиана равна константе)
Назначение. Используется для проверки предположения о том, что медиана выборки имеет какое-то определенное значение. Например, это может быть нормативное значение показателя, или же известно, каким оно должно быть у здоровых особей.
Нулевая гипотеза.
- H0: медиана = А против H1: медиана ¹ А. Гипотеза о равенстве медиан отвергается, если критериальное значение больше верхней a/2 % точки или ниже нижней a/2 % точки стандартного нормального распределения.
- H0: медиана £ А против H1: медиана > А. Нулевая гипотеза отвергается, если критериальное значение выше, чем верхняя a % точка стандартного нормального распределения.
- H0: медиана ³ А против H1: медиана < А. Нулевая гипотеза отвергается, если критериальное значение меньше нижней a% точки стандартного нормального распределения.
Предпосылки
- Наблюдения независимы и принадлежат одной генеральной совокупности.
Описание метода
- Рассчитываем количество выборочных значений (обозначим его K), которые больше А.
- Рассчитываем критериальное значение по формуле
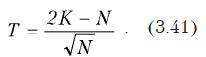
- Выполняем проверку гипотезы (см. выше).
Если количество наблюдений в выборке меньше 25, то в качестве критериального значения используется К, а сравнивают его с биномиальным распределением следующим образом.
- Для случая H0: медиана = А против H1: медиана ¹ А, гипотеза о равенстве медиан отвергается, если критериальное значение больше верхней a/2% точки или ниже нижней a/2 % точки биномиального распределения с параметрами (N; 0,5)
- Для случая H0: медиана £ А против H1: медиана > А, нулевая гипотеза отвергается, если критериальное значение выше, чем верхняя a% точка биномиального распределения с параметрами (N; 0,5).
- В случае H0: медиана ³ А против H1: медиана < А, нулевая гипотеза отвергается, если критериальное значение меньше нижней a% точки биномиального распределения с параметрами (N; 0,5).
Примечание:
- При малом числе экспериментов мощность критерия мала.
- Этот критерий может применяться и при нормальном законе распределения выборки.
Пример
Мы располагаем значениями показателей, полученных в результате проведения эксперимента (см. рис. 3.43,. столбец В). Известно, что медиана этого показателя должна быть равна 14. Необходимо проверить, можно ли считать, что для этой выборки медиана с доверительной вероятностью 0,95 равна 14.
Для проверки гипотезы выполним следующие действия.
- Строим столбец разностей (столбец С). Для этого помещаем в ячейку С2 формулу =B2–14, а затем размножаем ее на весь столбец.
- Строим вспомогательный столбец D, в котором помещается 1, если разница между значением и медианой положительна, и 0, если отрицательна. Для этого вводим в ячейку С2 формулу =ЕСЛИ(C2>0;1;0) , затем размножаем ее на весь столбец.
- Строим вспомогательный столбец E, в котором помещается 1, если разница не равна нулю, и 0, если равна нулю. Для этого вводим в ячейку С2 формулу =ЕСЛИ(C2<>0;1;0), затем размножаем ее на весь столбец. Этот столбец строится в том случае, если количество наблюдений меньше 25.
- Находим количество положительных значений (то есть таких, которые больше медианы) как сумму значений вспомогательного столбца D. Для этого в ячейку G6 вводится формула =СУММ(D2:D13). Это значение соответствует параметру К из формулы, приведенной в описании.
- Находим общее количество наблюдений, в которых значение не равно медиане. Для чего в ячейку G7 помещаем формулу =СУММ(E2:E13) (параметр N формулы). Если количество наблюдений больше 25, то в ячейку G7 вводим формулу =ЧСТРОК(В2:В13).
- Рассчитываем критериальное значение =(2*G6-G7)/КОРЕНЬ(G7). Это необходимо делать только когда количество наблюдений больше 25; в других случаях в качестве критериального значения используется К (см. п.4).
- Рассчитываем табличное значение. Поскольку число наблюдений меньше 25, то рассчитываются нижняя точка =КРИТБИНОМ(G7;0,5;0,025) и верхняя точка =КРИТБИНОМ(G7;0,5;0,975). Поскольку наше значение К = 4 находится в интервале между нижним (1) и верхним (6) критическими значениями, то нулевая гипотеза принимается.
Если число наблюдений больше 25, то в качестве нижнего критического значения берется =НОРМОБР(0,025;0;1), а верхнего — =НОРМОБР(0,975;0;1). Сравнение выполняется аналогично. Результаты применения данного критерия приведены на рис. 3.43.
3.3.11. Доверительный интервал для медианы, основанный на методе Уилкоксона (Тьюки)
Назначение. Используется для парных наблюдений. Позволяет построить доверительный интервал для разности пар.
Описание метода
Определение доверительного интервала с доверительной вероятностью р выполняется следующим образом.
- Находим целое число К (при расчете необходимо округлить) по формуле (3.42), где n — число пар наблюдений; — процентная точка распределения Стьюдента.
- Рассчитываем значения Wl = (Zi+Zj)/2, где Z — значение разности между парами значений по абсолютной величине. Wl находим для всех комбинаций пар (то есть 1-я с 1, 2, 3, …, n-й; затем 2-я с 2, 3, …, n-й и т.д.
- Полученные значения Wl упорядочиваем по возрастанию.
- Определяем левую и правую границы доверительного интервала. Левая граница равна элементу ранжированного ряда Wl с номером К, а правая — значению ряда с номером М+1–К. При этом (3.43)
Пример
Рассмотрим построение доверительного интервала (поиск его нижней и верхней границы), используя пример, приведенный в 3.1.5. Для этого необходимо применить пользовательскую функцию W_conf(K; R_1; R_2; t), текст которой приведен ниже. В зависимости от значения параметра t (0 или 1), данная функция вычисляет нижнюю (при t = 0) или верхнюю (при t = 1) границу доверительного интервала.
- Вставьте лист модуля и аккуратно введите текст функции W_conf(K; R_1; R_2; t) (см. 1.6).
Option Base 1
Function W_conf(K As Variant, R_1 As Object, R_2 As Object, t As Boolean) As Double
‘Вычисление доверительных интервалов на основе метода Уилкоксона
‘средних двух генеральных совокупностей связанных выборок
‘K — рассчитываемое значения номера элемента ряда
‘t — логическая переменная, принимающая следующие значения
‘ 0 — функция расчитывает нижнюю границу доверит. интервала
‘ 1 — функция расчитывает верхнюю границу доверит. интервала
‘R_1 — 1-й массив (1-я анализируемая выборка)
‘R_2 — 2-й массив (2-я анализируемая выборка)
Dim m_t()
Dim m_t2()
N_el = R_1.Count ‘вычисление количества элементов в выборке
n_range = N_el * (N_el + 1) / 2
ReDim m_t2(N_el)
ReDim m_t(n_range)
‘Вычисление абсолютных значений разностей
For i = 1 To N_el
m_t2(i) = Abs(R_2.Cells(i) — R_1.Cells(i))
Next i
‘Построение массива значений Wl
m = 0#
For i = 1 To N_el
For j = i To N_el
m = m + 1
m_t(m) = (m_t2(i) + m_t2(j)) / 2
Next j
Next i
‘ранжирование полученного массива значений,используя пузырьковый метод
Counter = 1 ‘ Инициализация индикатора перестановок.
While Counter = 1 ‘ Анализ значения индикатора перестановок.
Counter = 0
For i = 1 To n_range — 1
If m_t(i)>m_t(i+1) Then tp=m_t(i):m_t(i)=m_t(i+1):m_t(i+1)=tp: Counter=1
Next i
Wend
If t = False Then W_conf = m_t(n_range + 1 — K)
If t = True Then W_conf = m_t(K)
End Function
- Подготовьте таблицу данных и рассчитайте: значение n (размер выборки); (1-p)/2 (в нашем случае возьмем вероятность p = 0,95); значение (процентная точка распределения Стьюдента) и значение К (согласно формуле, приведенной выше). Координаты ячеек, формулы, внесенные в них, и вычисленные значения приведены в таблице 3.12.
Таблица 3.12 Формулы расчетов
| Координаты ячеек | В15 | В16 | В17 | В18 |
| Формулы | =СЧЁТЗ(B5:B14) | =(1-0,95) /2 | =СТЬЮДРАСПОБР(B16;B15) | =ОКРУГЛ((B15*(B15+ 1))/2+1-B17;0) |
| Значения | 10 | 0,025 | 2,633769327 | 53 |
- Вычислите границы доверительного интервала для медианы. Для этого в ячейку В19 введите =W_conf(B18;A5:A14;B5:B14;0) (вычисление нижней границы доверительного интервала), а в В20 поместите =W_conf(B18;A5:A14;B5:B14;1) (вычисление верхней границы доверительного интервала). В нашем случае нижняя граница доверительного интервала для медианы будет равна 2, а верхняя — 14,5. Полученные результаты приведены на рис. 3.44.
Рис. 3.44. Результаты расчета границ доверительных интервалов для медианы
3.3.12. Доверительный интервал для сдвига, основанный на методе Уилкоксона (Мозеса)
Назначение. Используется для двух независимых выборок. Позволяет построить доверительный интервал для сдвига, то есть для величины, которая отличает значения параметров сдвига в контрольной и экспериментальной выборках.
Описание метода
Определение доверительного интервала с доверительной вероятностью р выполняется следующим образом.
- Находим целое число К (при расчете необходимо округлить) по формуле (3.44), где m — количество наблюдений в первой выборке (значения Xi), а n — количество наблюдений во второй выборке (значения Yj); — верхняя процентная точка распределения Уилкоксона.
- Рассчитываем значения Ul = Yj – Xi, где Yj – Xi — значение разности между значениями первой и второй выборок. Ul находится для всех комбинаций пар (то есть 1-я с 1, 2, 3, …, m-й; затем 2-я с 1, 2, .. , m-й и т.д.
- Упорядочиваем по возрастающей значения Ul.
- Определяем левую и правую границы доверительного интервала. Левая граница равна элементу ранжированного ряда Ul с номером К, а правая — значению ряда с номером (nm+1–К).
Пример
Рассчитаем доверительные интервал для сдвига, используя данные примера, приведенные в подразделе 3.3.7. Для этого применим пользовательскую функцию W_conf2(K; R_1; R_2; t), текст которой приведен ниже.
Вставьте лист модуля и аккуратно введите текст функции W_conf2(K; R_1; R_2; t) (см. 1.6). Параметры данной функции имеют следующее назначение: K — целое число; R_1 — ссылка на ячейки первой выборки; R_2 — ссылка на ячейки второй выборки; t — параметр, принимающий значение 0 или 1. При t = 0 данная функция вычисляет нижнюю границу доверительного интервала для сдвига, а при t = 1 — верхнюю.
Option Base 1
Function W_conf2(K As Variant, R_1 As Object, R_2 As Object, t As Boolean) As Double
‘Вычисление доверительных интервалов для сдвига
‘основанный на методе Уилкоксона
‘K — рассчитываемое значения номера элемента ряда
‘t — логическая переменная, принимающая следующие значения
‘ 0 — функция расчитывает нижнюю границу доверит. интервала
‘ 1 — функция расчитывает верхнюю границу доверит. интервала
‘R_1 — контрольная выборка
‘R_2 — экспериментальная выборка
Dim m_t()
N_1 = R_1.Count ‘вычисление количества элементов в выборке
N_2 = R_2.Count ‘вычисление количества элементов в выборке
n_range = N_1 * N_2
ReDim m_t(n_range)
‘Построение массива значений Ul
‘MsgBox “Размеры массива “ & n_range
m = 0#
For i = 1 To N_2
For j = 1 To N_1
m = m + 1
m_t(m) = R_2.Cells(i) — R_1.Cells(j)
Next j
Next i
‘Ранжирование полученного массива значений,используя пузырьковый метод
Counter = 1 ‘ Инициализация индикатора перестановок.
While Counter = 1 ‘ Анализ значения индикатора перестановок.
Counter = 0
For i = 1 To n_range — 1
If m_t(i)>m_t(i+1) Then tp=m_t(i): m_t(i)=m_t(i+1): m_t(i+1)=tp: Counter=1
Next i
Wend
If t = False Then W_conf2 = m_t(K)
If t = True Then W_conf2 = m_t(N_1 * N_2 + 1 — K)
End Function
- Введем размеры обеих выборок N1 и N2, а также уровень значимости Q=1-p. В нашем случае N1 =12, N2 =13, Q = 0,05.
- Вычислим верхнее критическое значение статистики W, предварительно вычислив нижнее, используя формулы и пользовательскую функцию, описанные в подразделе 3.3.2. Для этого необходимо определить (если вы не сделали этого ранее) пользовательскую функцию Wperculc1(alfa; m_size; n_size). В ячейку введем D8 формулу =Wperculc1(D7/2;D5;D6) для расчета нижнего критического значение статистики W, а в ячейку D10 — формулу =D5*(D5+D6+1)-D8 для расчета верхнего критического значение статистики W. В результате получим, что w (1-p)/2, n1, n2 = 119, W(1-p)/2, n1, n2 = 193.
- Вычислим целое значение К (согласно формуле, приведенной выше). Для этого в ячейку G11 введем формулу =ОКРУГЛ(E6*(2*E6+E7+1)/2+1-E10;0). Целое число К примет значение 36.
- Вычислим границы доверительного интервала для сдвига. Для этого в ячейку G12 введем =W_conf2(G11;B5:B16;C5:C17;0) (вычисление нижней границы доверительного интервала), а в G13 поместим =W_conf2(G11;B5:B16;C5:C17;1) (вычисление верхней границы доверительного интервала). В нашем случае нижняя граница доверительного интервала для сдвига будет равна 14, а верхняя — 13. Полученные результаты приведены на рис. 3.45.
Рис. 3.45. Результаты расчета границ доверительных интервалов для сдвига
3.3.12. Множественные сравнения.
Для множественных сравнений имеются непараметрические критерии, которые выполняют ту же или сходную задачу, что и критерий Шеффе. К ним относятся критерии Пейджа и Холлендера для альтернатив с упорядочением; и множественные сравнения, основанные на ранговых суммах Фридмана. Собственно ту задачу, что и метод множественных сравнений Шеффе, решает как раз последний из них. Его мы и рассмотрим.
Пусть мы имеем k выборок, в каждой из которых n наблюдений. Т.е. мы имеем матрицу исходных данных, в которой n строк и k столбцов.
Построим ранги для каждой строки матрицы. После этого для каждого столбца находим сумму рангов
где rij – ранг i-го наблюдения в j-й выборке.
После этого строим k(k-1) разностей между суммами рангов, взятых по абсолютной величине , u<v.
Если выполняется условие , то с уровнем значимости a мы можем считать, что средние значения выборок с номерами u и v не равны.
удовлетворяет условию
В [24] имеется таблица для значений . Для иллюстрации фрагмент ее представлен в таблице 3.13.
Таблица 3.13 Некоторые значения для
| k=3 | k=4 | k=5 | ||||
| n | a | a | a | |||
| 4 | 7 | 0,042 | 10 | 0,026 | 13 | 0,020 |
| 5 | 8 | 0,039 | 11 | 0,037 | 14 | 0,040 |
| 6 | 9 | 0,029 | 12 | 0,037 | 15 | 0,049 |
| 7 | 10 | 0,023 | 13 | 0,037 | 17 | 0,033 |
| 8 | 10 | 0,039 | 14 | 0,034 | 18 | 0,036 |
| 9 | 10 | 0,048 | 15 | 0,032 | 19 | 0,037 |
| 10 | 11 | 0,037 | 15 | 0,046 | 20 | 0,038 |
| 11 | 11 | 0,049 | 16 | 0,041 | 21 | 0,038 |
| 12 | 12 | 0,038 | 17 | 0,038 | 22 | 0,038 |
| 13 | 13 | 0,049 | 18 | 0,032 | 23 | 0,035 |
| 14 | 13 | 0,038 | 18 | 0,038 | 24 | 0,034 |
| 15 | 13 | 0,047 | 19 | 0,042 | 24 | 0,045 |
Как вы видите, каждому значению соответствует свое значение a. Это связано с тем, что значения дискретны и рассчитываются по комбинаторным формулам для каждого сочетания n и k. Значение a при этом выбирается из фактически имеющихся. Выбирается наиболее подходящее по значению для проверки гипотезы.
Пример
Рассмотрим пример, представленный на рис. 3.46. Поскольку проверка не подтвердила, что закон распределения нормальный, мы не имеем права применять метод множественных сравнений Шеффе. Выполняем следующую последовательность действий.
- Строим ранги по каждой строке таблицы наблюдений. Для этого в ячейку Н2 помещаем формулу =Rank1(B2;$B2:$F2;1), которую затем размножаем перетягиванием на остальные ячейки.
- Находим суммы рангов по всем столбцам. Для этого в ячейку Н16 помещаем формулу =СУММ(H2:H14) (на остальные ячейки размножается перетягиванием).
- Составляем таблицу абсолютных разностей между суммами рангов столбцов. Для этого в ячейки H19, I20, J21, K22 помещаем формулы =ABS($H$16-I$16), =ABS($I$16-J$16), =ABS($J$16-K$16), =ABS($K$16-L$16). На остальные ячейки соответствующих строчек формулы размножаются перетягиванием. В результате мы получили таблицу, в которой в 19 строчке которой размещены абсолютные значения между суммой рангов первой выборки и всех остальных, в 20-й абсолютные значения между суммой рангов второй выборки и всех остальных и т.д.
- Проведем проверку. Для этого из таблицы 3.13. берем соответствующее значение для 5 выборок и 13 наблюдений. Это 23. Этому критериальному значению соответствует уровень значимости 0.035.
- Видно, что больше этого значения разности между первой и четвертой, первой и пятой; второй и четвертой, второй и пятой; третьей и пятой выборками. Это значит, что средние этих пар выборок статистически значимо различаются. Те пары, для которых абсолютное значение разницы меньше критериального, не различаются.
Рис. 3.46. Пример непараметрических множественных сравнений
Литература, рекомендуемая для изучения
- Большев Л.Н., Смирнов Н.В. Таблицы математической статистики.— 3-е изд.— М.: Наука, 1983.— 416 с.
- Браунли К.А. Статистическая теория и методология в науке и технике.— М.: Наука, 407 с.
- Гмурман В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для втузов. — М.: Высш. Шк., 1977. — 479 с.
- Гублер Е.В. Вычислительные методы анализа и распознавания патологических процессов. — М.: Медицина, 1978. — 296 с.
- Гублер Е.В., Генкин А.А. Применение непараметрических критериев в медико-биологических исследованиях. – М.: Медицина, 1973.– 159с.
- Закс Л. Статистическое оценивание. — М.: Статистика, 1976.— 598 с.
- Кимбл Г. Как правильно пользоваться статистикой.— М.: Финансы и статистика, 1982.— 294 с.
- Колкот Э. Проверка значимости. — М.: Статистика, 1978. — 128 с.
- Кохрен У. Методы выборочного исследования. — М.: Статистика, 1976. — 440 с.
- Кудрин А.Н., Пономарева Г.Т. Применение математики в экспериментальной и клинической медицине. — М.: Медицина, 1967. — 356 с.
- Лапач С.Н., Пасечник М.Ф., Чубенко А.В. Статистические методы в фармакологии и маркетинге фармацевтического рынка. — К.: ЗАТ “Укрспецмонтаж”, 1999. — 312 с.
- Ликеш И., Ляга Й. Основные таблицы математической статистики.— М.: Финансы и статистика, 1985.— 356 с.
- Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике — М.: Финансы и статистика, 1982. — 278 с.
- Петрович М.Л., Давыдович М.И. Статистическое оценивание и проверка гипотез на ЭВМ. — М.: Финансы и статистика, 1989. — 191 с.
- Плохинский Н.А. Алгоритмы биометрии. — М.: МГУ, 1980. — 150 с.
- Поллард Дж. Справочник по вычислительным методам статистики.— М.: Финансы и статистика, 1982.— 344 с.
- Рунион Р. Справочник по непараметрической статистике: Современный подход / Пер. с англ. Е.З. Демиденко; Предисл. Ю.Н. Тюрина.— М.: Финансы и статистика, 1982.— 198 с.
- Справочник по прикладной статистике: В 2 т. Т. 1: Пер. с англ. / Под ред. Э. Ллойда, У. Ледермана, Ю.Н. Тюрина.— М.: Финансы и статистика, 1989.— 510 с.
- Справочник по прикладной статистике В 2 т. Т. 2: Пер. с англ.— М.: Финансы и статистика, 1990.— 526 с.
- Спрент П. Как обращаться с цифрами, или статистика в действии / Пер. с англ. А.Ф. Якубова.— Мн.: Выcш. шк., 1983.— 271 с.
- Терентьев П.В., Ростова Н.С. Практимум по биометрии. — Л.: ЛГУ, 1977. — 152 с.
- Тюрин Ю.Н. Непараметрические методы статистики.— М.: Знание, 1978.— 64 с.
- Тюрин Ю.Н., Макаров А.А. Статистический анализ данных на компьютере. — М.: ИНФРА-М, 1998.— 528 с.
- Хеттманспертер Т. Статистические выводы, основанные на рангах. — М.: Финансы и статистика, 1987. — 334 с.
- Хилл А. Основы медицинской статистики. — М.: Медгиз, 1958. — 306 с.
- Холлендер М., Вулф Д.А. Непараметрические методы статистики.— М.: Финансы и статистика, 1983.— 518 с.
- Хургин Я.И. Как объять необъятное. — М.: Знание, 1985. — 192 с.
- Эльясберг П.Е. Измерительная информация: сколько ее нужно? как ее обрабатывать? — М.: Наука, 1983.— 208 с.